Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-09T04:38:39.421Z Has data issue: false hasContentIssue false
  • English
  • Français

On the mean convergence of Markov operators

Published online by Cambridge University Press:  20 January 2009

Robert E. Atalla
Robert E. Atalla
Affiliation:
Ohio University, Athens, Ohio 45701
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout the paper, T will be a Markov operator on C(X) (X compact T2), i.e. a continuous positive operator such that Te = e (e the unit function). P will be the set of Borel probability measures on X, which we shall often think of as linear functionals on C(X), and 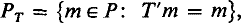, where T' is the adjoint of T. Let

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 2 , September 1974 , pp. 205 - 209
Copyright
Copyright © Edinburgh Mathematical Society 1974

References

REFERENCES

(1) Atalla, R., On the inclusion of a bounded convergence field in the space of almost convergent sequences, Glasgow Math. J. 13 (1972), 82–90.CrossRefGoogle Scholar
(2) Jamison, B., Ergodic decompositions induced by certain Markov operators, Trans. Amer. Math. Soc. 117 (1965), 451–468.CrossRefGoogle Scholar
(3) Leibowitz, G., Lectures on complex function algebras (Scott, Foresman and Company, Glenview, Illinois, 1970).Google Scholar
(4) Sine, R., Geometric theory of a single Markov operator, Pacific J. Math 27(1968), 155–166.CrossRefGoogle Scholar