Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T07:17:41.777Z Has data issue: false hasContentIssue false
  • English
  • Français

Representations of normed algebras with minimal left ideals

Published online by Cambridge University Press:  20 January 2009

Bruce A. Barnes
Bruce A. Barnes
Affiliation:
University of Oregon, Eugene, Oregon
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The theory of *-representations of Banach *-algebras on Hilbert space is one of the most useful and most successful parts of the theory of Banach algebras. However, there are only scattered results concerning the representations of general Banach algebras on Banach spaces. It may be that a comprehensive representation theory is impossible. Nevertheless, for some special algebras interesting and worthwhile results can be proved. This is true for 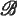(Y), the algebra of all bounded operators on a Banach space Y, and for 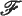(Y), the subalgebra of 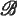(Y) consisting of operators with finite dimensional range. The representations of 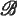(Y) are studied in a recent paper by H. Porta and E. Berkson (6), and in another recent paper (8), P. Chernoff determines the structure of the representations of 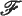(Y) (and also of some more general algebras of operators). In both these papers, 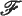(Y), which is the socle of the algebras under consideration, plays an important role in the theory. This suggests the possibility that a more general representation theory can be formulated in the case of a normed algebra with a nontrivial socle. This we attempt to do in this paper.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 2 , September 1974 , pp. 173 - 190
Copyright
Copyright © Edinburgh Mathematical Society 1974

References

REFERENCES

(1) Bachelis, G., Homomorphisms of annihilator Banach algebras, Pacific J. Math. 25 (1968), 229–247.CrossRefGoogle Scholar
(2) Barnes, B., Modular annihilator algebras, Canad. J. Math. 18 (1966), 566–578.CrossRefGoogle Scholar
(3) Barnes, B., Algebras with the spectral expansion property, Illinois J. Math. 11 (1967), 284–290.CrossRefGoogle Scholar
(4) Barnes, B., Irreducible algebras of operators which contain a minimal idem-potent, Proc. Amer. Math. Soc. 30 (1971), 337–342.Google Scholar
(5) Barnes, B., Density theorems for algebras of operators and annihilator Banach algebras, Michigan Math. J. 19 (1972), 149–155.CrossRefGoogle Scholar
(6) Berkson, E. and Porta, H., Representations of B(X), J. Functional Analysis 3 (1969), 1–34.CrossRefGoogle Scholar
(7) Bonsall, F. and Goldie, A., Annihilator algebras, Proc. London Math. Soc. (3) 4(1954), 154–167.CrossRefGoogle Scholar
(8) Chernoff, P., Representations, automorphisms, and derivations of some operator algebras, J. Functional Analysis 12 (1973), 275–289.CrossRefGoogle Scholar
(9) De Lamadrid, J. Gil, Topological modules: Banach algebras, tensor products, algebras of kernels, Trans. Amer. Math. Soc. 126 (1967), 361–419.CrossRefGoogle Scholar
(10) Grothendieck, A., Sur les applications linéaires faiblement compactes d'espaces du type C(K), Canad. J. Math. 5 (1953), 129–173.CrossRefGoogle Scholar
(11) Halmos, P., Introduction to Hilbert space and the theory of spectral multiplicity (Chelsea, New York, 1951).Google Scholar
(12) Hewitt, E. and Ross, K., Abstract harmonic analysis II (Springer-Verlag, Berlin, 1970).Google Scholar
(13) Jacobson, N., Structure of rings (Amer. Math. Soc. CoUoq. Publ., vol. 37, Amer. Math. Soc, Providence, R.I., 1956).CrossRefGoogle Scholar
(14) Kaplansky, I., Dual rings, Ann. of Math. (2) 49 (1948), 689–701.CrossRefGoogle Scholar
(15) Kaplansky, I., The structure of certain operator algebras, Trans. Amer. Math. Soc. 70 (1951), 219–255.CrossRefGoogle Scholar
(16) Loomis, L., An introduction to abstract harmonic analysis (Van Nostrand, Princeton N.J. 1953).Google Scholar
(17) Pelczynski, A., Projections in certain Banach spaces, Stadia Math. 19 (1960), 209–228.CrossRefGoogle Scholar
(18) Rjckart, C., General theory of Banach algebras (Van Nostrand, Princeton, N.J., 1960).Google Scholar