Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:28:05.577Z Has data issue: false hasContentIssue false
  • English
  • Français

A completeness theorem for a nonlinear problem

Published online by Cambridge University Press:  20 January 2009

K. J. Brown
K. J. Brown
Affiliation:
Heriot-Watt University, Edinburgh
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

As is well known, the linear Sturm-Liouville eigenvalue problem on a bounded real interval [a, b] possesses a family of eigenfunctions which is a complete orthonormal system for the real Hilbert space L2[a, b], i.e. there exists a sequence of eigenfunctions un such that (ui, uj) = δij (Kronecker delta) for i, j ∈ N (the set of positive integers) and, if u ∈ L2[a, b], u = 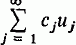where cj = (u, uj). Pimbley (4, p. 113), raises the question as to whether similar completeness results hold for nonlinear problems. In this note we show that certain nonlinear Sturm-Liouville eigenvalue problems possess eigenfunctions which form a basis for L2[a, b], i.e. there exists a sequence of eigenfunctions {vn} for the nonlinear problem such that every u ∈ L2[a, b] can be expressed in the form u = 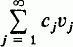by means of a unique sequence {cn} of real numbers.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 2 , September 1974 , pp. 169 - 172
Copyright
Copyright © Edinburgh Mathematical Society 1974

References

REFERENCES

(1) Crandall, M. G. and Rabinowitz, P. H., Bifurcation from simple eigenvalues, J. Functional Analysis 8 (1971), 321–340.CrossRefGoogle Scholar
(2) Everitt, W. N., On the limit point classification of second order differential operators, J. London Math. Soc. 41 (1966), 531–34.CrossRefGoogle Scholar
(3) Kato, T., Perturbation theory for linear operators (Springer Verlag, 1966).Google Scholar
(4) Pimbley, G. H., Eigenfunction branches of nonlinear operators and their bi-furcations (Springer Verlag, 1969).CrossRefGoogle Scholar
(5) Stuart, C. A., Some bifurcation theory for k-set contractions, Proc. London Math. Soc. 27 (1973), 531–550.CrossRefGoogle Scholar
(6) Titchmarsh, E. C., Eigenfunction expansions, Part 1 (Oxford University Press, 1946).Google Scholar