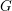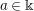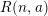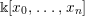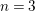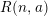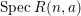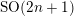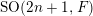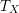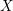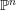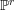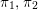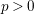Article
ON EXISTENCE OF CANONICAL
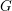 $G$-BASES
$G$-BASES
- Part of:
-
- Published online by Cambridge University Press:
- 15 September 2017, pp. 1-31
-
- Article
-
- You have access
- HTML
- Export citation
A NEW FAMILY OF POISSON ALGEBRAS AND THEIR DEFORMATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 25 September 2017, pp. 32-86
-
- Article
-
- You have access
- HTML
- Export citation
REPRÉSENTATIONS DE RÉDUCTION UNIPOTENTE POUR
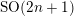 $\operatorname{SO}(2n+1)$, II : ENDOSCOPIE
$\operatorname{SO}(2n+1)$, II : ENDOSCOPIE
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2017, pp. 87-154
-
- Article
-
- You have access
- HTML
- Export citation
CHARACTERIZATION OF PROJECTIVE SPACES AND
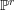 $\mathbb{P}^{r}$-BUNDLES AS AMPLE DIVISORS
$\mathbb{P}^{r}$-BUNDLES AS AMPLE DIVISORS
- Part of:
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 155-169
-
- Article
-
- You have access
- HTML
- Export citation
TEST VECTORS FOR LOCAL CUSPIDAL RANKIN–SELBERG INTEGRALS
- Part of:
-
- Published online by Cambridge University Press:
- 12 September 2017, pp. 170-192
-
- Article
-
- You have access
- HTML
- Export citation
CANONICAL LIFTS OF FAMILIES OF ELLIPTIC CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 193-213
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
NMJ volume 233 Cover and Front matter
-
- Published online by Cambridge University Press:
- 21 January 2019, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
NMJ volume 233 Cover and Back matter
-
- Published online by Cambridge University Press:
- 21 January 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation