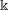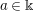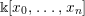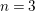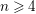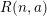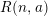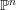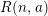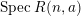1 Introduction
One of the fundamental notions of noncommutative algebraic geometry is that the noncommutative analogues of polynomial rings (or, alternatively, the coordinate rings of “noncommutative projective spaces”) are algebras which are Artin–Schelter regular [Reference Artin and SchelterAS87]. Constructing and, if possible, classifying, Artin–Schelter regular algebras of various global dimensions is thus one of the core problems in the subject. Within the class of quadratic Artin–Schelter regular algebras one also seeks to construct those which are Calabi–Yau in the sense of Ginzburg [Reference GinzburgGin06]. In general, the problem of classifying Artin–Schelter regular algebras (or Calabi–Yau algebras) is unsolved, even for global dimension 4.
In 2014, Brent Pym classified 4-dimensional Calabi–Yau algebras arising as deformation quantizations of torus-invariant Poisson structures on
![]() $\mathbb{A}_{\mathbb{C}}^{4}$
. He showed that there are six families of Calabi–Yau algebras which arise this way; the most interesting example has generators
$\mathbb{A}_{\mathbb{C}}^{4}$
. He showed that there are six families of Calabi–Yau algebras which arise this way; the most interesting example has generators
![]() $x_{0},x_{1},x_{2},x_{3}$
and relations
$x_{0},x_{1},x_{2},x_{3}$
and relations
 $$\begin{eqnarray}\left.\begin{array}{@{}ccl@{}}[x_{0},x_{1}]\, & =\, & 5x_{0}^{2}\\ \hspace{0.0pt}[x_{0},x_{2}]\, & =\, & -{\textstyle \frac{45}{2}}x_{0}^{2}+5x_{0}x_{1}\\ \hspace{0.0pt}[x_{0},x_{3}]\, & =\, & {\textstyle \frac{195}{2}}x_{0}^{2}-{\textstyle \frac{45}{2}}x_{0}x_{1}+5x_{0}x_{2}\\ \hspace{0.0pt}[x_{1},x_{2}]\, & =\, & -{\textstyle \frac{3}{2}}x_{0}x_{1}+3x_{0}x_{2}+x_{1}^{2}\\ \hspace{0.0pt}[x_{1},x_{3}]\, & =\, & 5x_{0}x_{1}-3x_{0}x_{2}+7x_{0}x_{3}-{\textstyle \frac{5}{2}}x_{1}^{2}+x_{1}x_{2}\\ \hspace{0.0pt}[x_{2},x_{3}]\, & =\, & -{\textstyle \frac{77}{2}}x_{0}x_{2}-{\textstyle \frac{77}{2}}x_{0}x_{3}+{\textstyle \frac{21}{2}}x_{1}x_{2}+7x_{1}x_{3}-3x_{2}^{2}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}ccl@{}}[x_{0},x_{1}]\, & =\, & 5x_{0}^{2}\\ \hspace{0.0pt}[x_{0},x_{2}]\, & =\, & -{\textstyle \frac{45}{2}}x_{0}^{2}+5x_{0}x_{1}\\ \hspace{0.0pt}[x_{0},x_{3}]\, & =\, & {\textstyle \frac{195}{2}}x_{0}^{2}-{\textstyle \frac{45}{2}}x_{0}x_{1}+5x_{0}x_{2}\\ \hspace{0.0pt}[x_{1},x_{2}]\, & =\, & -{\textstyle \frac{3}{2}}x_{0}x_{1}+3x_{0}x_{2}+x_{1}^{2}\\ \hspace{0.0pt}[x_{1},x_{3}]\, & =\, & 5x_{0}x_{1}-3x_{0}x_{2}+7x_{0}x_{3}-{\textstyle \frac{5}{2}}x_{1}^{2}+x_{1}x_{2}\\ \hspace{0.0pt}[x_{2},x_{3}]\, & =\, & -{\textstyle \frac{77}{2}}x_{0}x_{2}-{\textstyle \frac{77}{2}}x_{0}x_{3}+{\textstyle \frac{21}{2}}x_{1}x_{2}+7x_{1}x_{3}-3x_{2}^{2}.\end{array}\right.\end{eqnarray}$$
In this paper we generalize Pym’s example to arbitrary dimensions, and study the properties of the resulting algebras. In particular, we obtain new examples of Calabi–Yau algebras in all global dimensions
![]() ${\geqslant}5$
.
${\geqslant}5$
.
Pym’s example comes from an action of the 2-dimensional solvable Lie algebra on
![]() $\mathbb{C}[x_{0},x_{1},x_{2},x_{3}]$
, inducing a Poisson bracket. He shows, using a deformation formula of Coll, Gerstenhaber, and Giaquinto, that this Poisson bracket quantizes to give the algebra (1.1). We generalize Pym’s methods to construct a family of algebras
$\mathbb{C}[x_{0},x_{1},x_{2},x_{3}]$
, inducing a Poisson bracket. He shows, using a deformation formula of Coll, Gerstenhaber, and Giaquinto, that this Poisson bracket quantizes to give the algebra (1.1). We generalize Pym’s methods to construct a family of algebras
![]() $R(n,a)$
, depending on a scalar
$R(n,a)$
, depending on a scalar
![]() $a$
and an integer
$a$
and an integer
![]() $n\geqslant 1$
. The
$n\geqslant 1$
. The
![]() $R(n,a)$
are graded, quadratic, Noetherian, AS-regular domains of global dimension
$R(n,a)$
are graded, quadratic, Noetherian, AS-regular domains of global dimension
![]() $n+1$
(Theorem 3.8, Proposition 3.15). When
$n+1$
(Theorem 3.8, Proposition 3.15). When
![]() $n=3$
and
$n=3$
and
![]() $a=-{\textstyle \frac{5}{4}}$
we obtain Pym’s algebra (1.1). For another example,
$a=-{\textstyle \frac{5}{4}}$
we obtain Pym’s algebra (1.1). For another example,
![]() $R(1,a)$
is isomorphic to the Jordan plane
$R(1,a)$
is isomorphic to the Jordan plane
![]() $\mathbb{C}\langle x,y\rangle /(xy-yx-x^{2})$
(if
$\mathbb{C}\langle x,y\rangle /(xy-yx-x^{2})$
(if
![]() $a\neq 0$
) or to the polynomial ring
$a\neq 0$
) or to the polynomial ring
![]() $\mathbb{C}[x,y]$
(if
$\mathbb{C}[x,y]$
(if
![]() $a=0$
).
$a=0$
).
For each
![]() $n$
, there is one algebra
$n$
, there is one algebra
![]() $R(n,a)$
that is Calabi–Yau (Definition 4.14). We have:
$R(n,a)$
that is Calabi–Yau (Definition 4.14). We have:
Theorem 1.2. (Corollary 4.17)
The algebra
![]() $R(n,a)$
is Calabi–Yau if and only if
$R(n,a)$
is Calabi–Yau if and only if
Example (1.1) is the algebra arising from Theorem 1.2 when
![]() $n=3$
. The examples for
$n=3$
. The examples for
![]() $n\geqslant 4$
have not to our knowledge been studied before.
$n\geqslant 4$
have not to our knowledge been studied before.
Each
![]() $R(n,a)$
induces a Poisson bracket
$R(n,a)$
induces a Poisson bracket
![]() $\{-,-\}_{a}$
on
$\{-,-\}_{a}$
on
![]() $\mathbb{C}[x_{0},\ldots ,x_{n}]$
in the semiclassical limit. Let
$\mathbb{C}[x_{0},\ldots ,x_{n}]$
in the semiclassical limit. Let
![]() $A(n,a)$
be the Poisson algebra
$A(n,a)$
be the Poisson algebra
![]() $(\mathbb{C}[x_{0},\ldots ,x_{n}],\{-,-\}_{a})$
. In such a deformation-quantization context it is often expected that the algebra
$(\mathbb{C}[x_{0},\ldots ,x_{n}],\{-,-\}_{a})$
. In such a deformation-quantization context it is often expected that the algebra
![]() $R(n,a)$
and the Poisson algebra
$R(n,a)$
and the Poisson algebra
![]() $A(n,a)$
share similarities. For instance we make a detailed study of the prime spectrum
$A(n,a)$
share similarities. For instance we make a detailed study of the prime spectrum
![]() $\operatorname{Spec}R(n,a)$
of
$\operatorname{Spec}R(n,a)$
of
![]() $R(n,a)$
and the Poisson prime spectrum
$R(n,a)$
and the Poisson prime spectrum
![]() $\operatorname{PSpec}A(n,a)$
of
$\operatorname{PSpec}A(n,a)$
of
![]() $A(n,a)$
and show that they are homeomorphic (Theorem 7.1). We further investigate the structure of this space and prove:
$A(n,a)$
and show that they are homeomorphic (Theorem 7.1). We further investigate the structure of this space and prove:
Theorem 1.3. (Corollary 7.6)
Let
![]() $n\geqslant 3$
. The space
$n\geqslant 3$
. The space
![]() $\operatorname{Spec}R(n,a)\cong \operatorname{PSpec}A(n,a)$
is a union of quasiprojective strata, and has dimension
$\operatorname{Spec}R(n,a)\cong \operatorname{PSpec}A(n,a)$
is a union of quasiprojective strata, and has dimension
Moreover, we show that
![]() $R(n,a)$
satisfies the Dixmier–Moeglin equivalence (Theorem 8.3) and, using a transfer result, we prove that
$R(n,a)$
satisfies the Dixmier–Moeglin equivalence (Theorem 8.3) and, using a transfer result, we prove that
![]() $A(n,a)$
satisfies the Poisson Dixmier–Moeglin equivalence (Theorem 8.6). Taking advantage of the fact that
$A(n,a)$
satisfies the Poisson Dixmier–Moeglin equivalence (Theorem 8.6). Taking advantage of the fact that
![]() $\operatorname{Spec}R(n,a)\cong \operatorname{PSpec}A(n,a)$
we compute many examples of prime spectra of the
$\operatorname{Spec}R(n,a)\cong \operatorname{PSpec}A(n,a)$
we compute many examples of prime spectra of the
![]() $R(n,a)$
.
$R(n,a)$
.
We investigate various ring theoretic properties of the rings
![]() $R(n,a)$
and
$R(n,a)$
and
![]() $A(n,a)$
. For
$A(n,a)$
. For
![]() $n\geqslant 2$
we show that
$n\geqslant 2$
we show that
![]() $R(n,a)\cong R(n,b)$
if and only if
$R(n,a)\cong R(n,b)$
if and only if
![]() $A(n,a)$
is Poisson isomorphic to
$A(n,a)$
is Poisson isomorphic to
![]() $A(n,b)$
if and only if
$A(n,b)$
if and only if
![]() $a=b$
(Theorem 5.1). We compute the skewfield of fractions of
$a=b$
(Theorem 5.1). We compute the skewfield of fractions of
![]() $R(n,a)$
and show that it is isomorphic to a Weyl skewfield if and only if
$R(n,a)$
and show that it is isomorphic to a Weyl skewfield if and only if
![]() $a\in \mathbb{Q}$
(Theorem 8.11). We also show that the graded automorphism group of
$a\in \mathbb{Q}$
(Theorem 8.11). We also show that the graded automorphism group of
![]() $R(n,a)$
is isomorphic to the graded Poisson automorphism group of
$R(n,a)$
is isomorphic to the graded Poisson automorphism group of
![]() $A(n,a)$
.
$A(n,a)$
.
Finally, we compute the point modules of the
![]() $R(n,a)$
. We show:
$R(n,a)$
. We show:
Theorem 1.4. (Theorem 6.1)
Let
![]() $n\geqslant 1$
. For any
$n\geqslant 1$
. For any
![]() $a$
, the point schemes of
$a$
, the point schemes of
![]() $R(n,a)$
are isomorphic. The point modules of
$R(n,a)$
are isomorphic. The point modules of
![]() $R=R(n,a)$
are parameterized by the union
$R=R(n,a)$
are parameterized by the union
![]() $C_{1}\cup \cdots \cup C_{n}$
, where
$C_{1}\cup \cdots \cup C_{n}$
, where
![]() $C_{k}$
is a rational normal curve of degree
$C_{k}$
is a rational normal curve of degree
![]() $k$
in
$k$
in
![]() $\mathbb{P}(R_{1}^{\ast })\cong \mathbb{P}^{n}$
.
$\mathbb{P}(R_{1}^{\ast })\cong \mathbb{P}^{n}$
.
As with Pym’s original example, these curves correspond to various nice (equivariant with respect to the appropriate group action) ways to embed
![]() $\mathbb{P}^{1}$
in
$\mathbb{P}^{1}$
in
![]() $\operatorname{Sym}^{n}(\mathbb{P}^{1})\cong \mathbb{P}^{n}$
.
$\operatorname{Sym}^{n}(\mathbb{P}^{1})\cong \mathbb{P}^{n}$
.
The organization of the paper is as follows. In Section 2 we define the
![]() $R(n,a)$
and
$R(n,a)$
and
![]() $A(n,a)$
, and in Section 3 we prove that
$A(n,a)$
, and in Section 3 we prove that
![]() $A(n,a)$
is the associated graded ring of
$A(n,a)$
is the associated graded ring of
![]() $R(n,a)$
and that
$R(n,a)$
and that
![]() $R(n,a)$
is an Artin–Schelter regular Noetherian domain. We prove Theorem 1.2 in Section 4, and also calculate the graded automorphism group of
$R(n,a)$
is an Artin–Schelter regular Noetherian domain. We prove Theorem 1.2 in Section 4, and also calculate the graded automorphism group of
![]() $R(n,a)$
and the graded Poisson automorphism group of
$R(n,a)$
and the graded Poisson automorphism group of
![]() $A(n,a)$
. We study when two
$A(n,a)$
. We study when two
![]() $R(n,a)$
are isomorphic in Section 5 and prove Theorem 1.3 in Section 6.
$R(n,a)$
are isomorphic in Section 5 and prove Theorem 1.3 in Section 6.
In the final three sections we describe the (Poisson) prime and primitive ideals of
![]() $R(n,a)$
and
$R(n,a)$
and
![]() $A(n,a)$
. We prove Theorem 1.4 in Section 7. In Section 8 we show that
$A(n,a)$
. We prove Theorem 1.4 in Section 7. In Section 8 we show that
![]() $R(n,a)$
satisfies the Dixmier–Moeglin equivalence describing primitive ideals, and that
$R(n,a)$
satisfies the Dixmier–Moeglin equivalence describing primitive ideals, and that
![]() $A(n,a)$
satisfies the related Poisson Dixmier–Moeglin equivalence. We also compute the fraction skewfield of
$A(n,a)$
satisfies the related Poisson Dixmier–Moeglin equivalence. We also compute the fraction skewfield of
![]() $R(n,a)$
. Finally, in Section 9 we give many explicit examples of prime spectra.
$R(n,a)$
. Finally, in Section 9 we give many explicit examples of prime spectra.
2 Notation and definitions
Throughout we work over a field
![]() $\Bbbk$
of characteristic zero (in the introduction for simplicity we worked over
$\Bbbk$
of characteristic zero (in the introduction for simplicity we worked over
![]() $\mathbb{C}$
).
$\mathbb{C}$
).
In this section we define the algebras
![]() $R(n,a)$
and the Poisson algebras
$R(n,a)$
and the Poisson algebras
![]() $A(n,a)$
that are the subject of the paper, and describe how they arise from
$A(n,a)$
that are the subject of the paper, and describe how they arise from
![]() $\Bbbk ^{\times }$
-invariant actions of the 2-dimensional solvable Lie algebra on polynomial rings.
$\Bbbk ^{\times }$
-invariant actions of the 2-dimensional solvable Lie algebra on polynomial rings.
We begin by discussing such actions. Fix an integer
![]() $n\in \mathbb{Z}_{{>}0}$
, and let
$n\in \mathbb{Z}_{{>}0}$
, and let
![]() $\unicode[STIX]{x1D6E5}$
be the “downward derivation”
$\unicode[STIX]{x1D6E5}$
be the “downward derivation”
(where
![]() $\unicode[STIX]{x2202}_{i}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}X_{i}$
). For
$\unicode[STIX]{x2202}_{i}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}X_{i}$
). For
![]() $a_{0},\ldots ,a_{n}\in \Bbbk$
, let
$a_{0},\ldots ,a_{n}\in \Bbbk$
, let
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}(a_{0},\ldots ,a_{n})$
be the weighted Euler operator
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}(a_{0},\ldots ,a_{n})$
be the weighted Euler operator
We are interested in when
![]() $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
![]() $\unicode[STIX]{x1D6E4}$
generate a copy of the 2-dimensional solvable Lie algebra inside
$\unicode[STIX]{x1D6E4}$
generate a copy of the 2-dimensional solvable Lie algebra inside
![]() $\operatorname{Der}_{\Bbbk }(\Bbbk [X_{0},\ldots ,X_{n}])$
.
$\operatorname{Der}_{\Bbbk }(\Bbbk [X_{0},\ldots ,X_{n}])$
.
Lemma 2.1. We have
![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6E4}-\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}$
if and only if
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6E4}-\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}$
if and only if
![]() $a_{j}=a_{0}+j$
for
$a_{j}=a_{0}+j$
for
![]() $j\in \{0,\ldots ,n\}$
.
$j\in \{0,\ldots ,n\}$
.
Proof. This follows from the computation
so
![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6E4}-\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}$
if and only if
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6E4}-\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}$
if and only if
![]() $a_{i+1}=a_{i}+1$
for all
$a_{i+1}=a_{i}+1$
for all
![]() $i$
.◻
$i$
.◻
The importance of Lemma 2.1 is the following result of [Reference PymPym15], based on the universal deformation formula of [Reference Coll, Gerstenhaber and GiaquintoCGG89].
Proposition 2.2. [Reference PymPym15, Lemma 3.3]
Let
![]() $A$
be a commutative
$A$
be a commutative
![]() $\Bbbk$
-algebra, and let
$\Bbbk$
-algebra, and let
![]() $\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E4}:A\rightarrow A$
be
$\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E4}:A\rightarrow A$
be
![]() $\Bbbk$
-derivations so that
$\Bbbk$
-derivations so that
![]() $\unicode[STIX]{x1D6E5}$
is locally nilpotent and
$\unicode[STIX]{x1D6E5}$
is locally nilpotent and
![]() $[\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E4}]=\unicode[STIX]{x1D6E5}$
. For
$[\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D6E4}]=\unicode[STIX]{x1D6E5}$
. For
![]() $k\in \mathbb{N}$
, define
$k\in \mathbb{N}$
, define
![]() $\binom{\unicode[STIX]{x1D6E4}}{k}=(1/k!)\unicode[STIX]{x1D6E4}\cdot (\unicode[STIX]{x1D6E4}-1)\cdots (\unicode[STIX]{x1D6E4}-(k-1))$
. Then
$\binom{\unicode[STIX]{x1D6E4}}{k}=(1/k!)\unicode[STIX]{x1D6E4}\cdot (\unicode[STIX]{x1D6E4}-1)\cdots (\unicode[STIX]{x1D6E4}-(k-1))$
. Then
defines an associative product on
![]() $A[\hbar ]$
whose semiclassical limit as
$A[\hbar ]$
whose semiclassical limit as
![]() $\hbar \rightarrow 0$
is the Poisson bracket
$\hbar \rightarrow 0$
is the Poisson bracket
Further, evaluating at a particular
![]() $\hbar \in \Bbbk$
gives an associative product
$\hbar \in \Bbbk$
gives an associative product
The rings
![]() $(A,\ast _{\hbar })$
are isomorphic for any
$(A,\ast _{\hbar })$
are isomorphic for any
![]() $\hbar \neq 0$
.Footnote
1
$\hbar \neq 0$
.Footnote
1
Thus let
![]() $A=\Bbbk [X_{0},\ldots ,X_{n}]$
. For
$A=\Bbbk [X_{0},\ldots ,X_{n}]$
. For
![]() $a\in \Bbbk$
, define
$a\in \Bbbk$
, define
Let
![]() $\ast _{a}:A\otimes _{\Bbbk }A\rightarrow A$
be defined by
$\ast _{a}:A\otimes _{\Bbbk }A\rightarrow A$
be defined by
By Lemma 2.1 and Proposition 2.2, this defines an associative multiplication on
![]() $A$
. Let
$A$
. Let
![]() $\{-,-\}_{a}:A\otimes _{\Bbbk }A\rightarrow A$
be the associated Poisson bracket
$\{-,-\}_{a}:A\otimes _{\Bbbk }A\rightarrow A$
be the associated Poisson bracket
Going forward, we define
![]() $R(n,a)$
to be the associative algebra
$R(n,a)$
to be the associative algebra
![]() $(A,\ast _{a})$
and
$(A,\ast _{a})$
and
![]() $A(n,a)$
to be the Poisson algebra
$A(n,a)$
to be the Poisson algebra
![]() $(A,\{-,-\}_{a})$
. The goal of this paper is to study these two algebras.
$(A,\{-,-\}_{a})$
. The goal of this paper is to study these two algebras.
To end the section, we describe how the construction above relates to the canonical action of the standard Borel subgroup of
![]() $\mathbb{P}\text{GL}_{2}(\Bbbk )$
on
$\mathbb{P}\text{GL}_{2}(\Bbbk )$
on
![]() $\mathbb{P}^{1}$
. Let
$\mathbb{P}^{1}$
. Let
be the standard Borel subgroup of
![]() $\mathbb{P}\text{GL}_{2}(\Bbbk )$
. Note that
$\mathbb{P}\text{GL}_{2}(\Bbbk )$
. Note that
![]() $G\cong \Bbbk \rtimes \Bbbk ^{\times }$
and is the subgroup of
$G\cong \Bbbk \rtimes \Bbbk ^{\times }$
and is the subgroup of
![]() $\mathbb{P}\text{GL}_{2}(\Bbbk )$
that fixes the point
$\mathbb{P}\text{GL}_{2}(\Bbbk )$
that fixes the point
![]() $\infty =[1:0]\in \mathbb{P}^{1}$
.
$\infty =[1:0]\in \mathbb{P}^{1}$
.
The group
![]() $G$
acts on
$G$
acts on
![]() $\operatorname{Sym}^{n}(\mathbb{P}^{1})\cong \mathbb{P}^{n}$
and thus on the homogeneous coordinate ring
$\operatorname{Sym}^{n}(\mathbb{P}^{1})\cong \mathbb{P}^{n}$
and thus on the homogeneous coordinate ring
![]() $B(\mathbb{P}^{n},{\mathcal{O}}(1))\cong \Bbbk [X_{0},\ldots ,X_{n}]$
. Thus the 2-dimensional solvable Lie algebra
$B(\mathbb{P}^{n},{\mathcal{O}}(1))\cong \Bbbk [X_{0},\ldots ,X_{n}]$
. Thus the 2-dimensional solvable Lie algebra
![]() $\operatorname{Lie}G$
acts by derivations on
$\operatorname{Lie}G$
acts by derivations on
![]() $\Bbbk [X_{0},\ldots ,X_{n}]$
for all
$\Bbbk [X_{0},\ldots ,X_{n}]$
for all
![]() $n$
. All of these actions are induced by taking symmetric powers of the standard action on
$n$
. All of these actions are induced by taking symmetric powers of the standard action on
![]() $\mathbb{V}=\Bbbk \cdot \{X,Y\}$
.
$\mathbb{V}=\Bbbk \cdot \{X,Y\}$
.
To see how this works explicitly, fix
![]() $a\in \Bbbk$
and let
$a\in \Bbbk$
and let
![]() $\unicode[STIX]{x1D6E4}_{a}=aX\unicode[STIX]{x2202}_{X}+(a+1)Y\unicode[STIX]{x2202}_{Y}$
and
$\unicode[STIX]{x1D6E4}_{a}=aX\unicode[STIX]{x2202}_{X}+(a+1)Y\unicode[STIX]{x2202}_{Y}$
and
![]() $\unicode[STIX]{x1D6E5}=X\unicode[STIX]{x2202}_{Y}$
as above. Fix also
$\unicode[STIX]{x1D6E5}=X\unicode[STIX]{x2202}_{Y}$
as above. Fix also
![]() $n\geqslant 1$
. If we set
$n\geqslant 1$
. If we set
![]() $X_{j}=X^{n-j}Y^{j}/j!$
then
$X_{j}=X^{n-j}Y^{j}/j!$
then
![]() $X_{0},\ldots ,X_{n}$
form a basis for
$X_{0},\ldots ,X_{n}$
form a basis for
![]() $\operatorname{Sym}^{n}(\mathbb{V})$
with
$\operatorname{Sym}^{n}(\mathbb{V})$
with
![]() $\unicode[STIX]{x1D6E5}(X_{j})=X_{j-1}$
and
$\unicode[STIX]{x1D6E5}(X_{j})=X_{j-1}$
and
![]() $\unicode[STIX]{x1D6E4}_{a}(X_{j})=((n-j)a+j(a+1))X_{j}=(na+j)X_{j}$
. We see that
$\unicode[STIX]{x1D6E4}_{a}(X_{j})=((n-j)a+j(a+1))X_{j}=(na+j)X_{j}$
. We see that
![]() $n$
th symmetric power of the bracket
$n$
th symmetric power of the bracket
![]() $\{-,-\}_{a}$
on
$\{-,-\}_{a}$
on
![]() $\Bbbk [X,Y]$
induces
$\Bbbk [X,Y]$
induces
![]() $\{-,-\}_{na}$
on
$\{-,-\}_{na}$
on
![]() $\Bbbk [X_{0},\ldots ,X_{n}]$
.
$\Bbbk [X_{0},\ldots ,X_{n}]$
.
Consider the surjection
![]() $\unicode[STIX]{x1D719}:\Bbbk [X_{0},\ldots ,X_{n}]{\twoheadrightarrow}\Bbbk [X_{0},X_{1}]^{(n)}$
induced from the Veronese embedding of
$\unicode[STIX]{x1D719}:\Bbbk [X_{0},\ldots ,X_{n}]{\twoheadrightarrow}\Bbbk [X_{0},X_{1}]^{(n)}$
induced from the Veronese embedding of
![]() $\mathbb{P}^{1}$
as a rational normal curve in
$\mathbb{P}^{1}$
as a rational normal curve in
![]() $\mathbb{P}^{n}$
. The Veronese embedding is
$\mathbb{P}^{n}$
. The Veronese embedding is
![]() $G$
-equivariant by construction, and from the discussion above we expect
$G$
-equivariant by construction, and from the discussion above we expect
![]() $\unicode[STIX]{x1D719}$
to be a Poisson homomorphism from
$\unicode[STIX]{x1D719}$
to be a Poisson homomorphism from
![]() $A(n,a)\rightarrow A(1,a/n)^{(n)}$
. We see in Section 6 that this does happen, and furthermore that there is also a surjection
$A(n,a)\rightarrow A(1,a/n)^{(n)}$
. We see in Section 6 that this does happen, and furthermore that there is also a surjection
![]() $R(n,a)\rightarrow R(1,a/n)^{(n)}$
.
$R(n,a)\rightarrow R(1,a/n)^{(n)}$
.
3 First properties
Fix
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $a\in \Bbbk$
, and let
$a\in \Bbbk$
, and let
![]() $A=A(n,a)$
and
$A=A(n,a)$
and
![]() $R=R(n,a)$
. In this section, we give an explicit presentation of
$R=R(n,a)$
. In this section, we give an explicit presentation of
![]() $R$
. We show that
$R$
. We show that
![]() $R$
is a Noetherian Artin–Schelter regular domain of global dimension
$R$
is a Noetherian Artin–Schelter regular domain of global dimension
![]() $n+1$
. Finally we study the localizations of
$n+1$
. Finally we study the localizations of
![]() $A$
and
$A$
and
![]() $R$
at the (Poisson) normal element
$R$
at the (Poisson) normal element
![]() $X_{0}$
.
$X_{0}$
.
In the following, we suppress the subscript
![]() $a$
where it is clear from context, so we use
$a$
where it is clear from context, so we use
![]() $\ast$
to denote multiplication in
$\ast$
to denote multiplication in
![]() $R$
and
$R$
and
![]() $\{-,-\}$
to denote the Poisson bracket on
$\{-,-\}$
to denote the Poisson bracket on
![]() $A$
. We use concatenation to denote the (commutative) multiplication in
$A$
. We use concatenation to denote the (commutative) multiplication in
![]() $A$
.
$A$
.
Let
![]() $z_{j}=a+j$
and set
$z_{j}=a+j$
and set
![]() $X_{-1}:=0$
. Since
$X_{-1}:=0$
. Since
![]() $\binom{\unicode[STIX]{x1D6E4}_{a}}{\ell }(X_{j})=\binom{a+j}{\ell }X_{j}$
we deduce from (2.3) that, for all
$\binom{\unicode[STIX]{x1D6E4}_{a}}{\ell }(X_{j})=\binom{a+j}{\ell }X_{j}$
we deduce from (2.3) that, for all
![]() $0\leqslant i,j\leqslant n$
, we have:
$0\leqslant i,j\leqslant n$
, we have:
and
We use two gradings on
![]() $A$
: the standard degree grading
$A$
: the standard degree grading
![]() $d$
defined by
$d$
defined by
![]() $d(X_{i})=1$
for all
$d(X_{i})=1$
for all
![]() $i$
and the weight grading
$i$
and the weight grading
![]() $\unicode[STIX]{x1D716}$
defined by
$\unicode[STIX]{x1D716}$
defined by
![]() $\unicode[STIX]{x1D716}(X_{i})=i$
. For
$\unicode[STIX]{x1D716}(X_{i})=i$
. For
![]() $k\in \mathbb{N}$
, let
$k\in \mathbb{N}$
, let
![]() $A_{k}$
be the
$A_{k}$
be the
![]() $d$
-homogeneous component of
$d$
-homogeneous component of
![]() $d$
-degree
$d$
-degree
![]() $k$
, and let
$k$
, and let
![]() $A^{k}$
be the
$A^{k}$
be the
![]() $\unicode[STIX]{x1D716}$
-homogeneous component of
$\unicode[STIX]{x1D716}$
-homogeneous component of
![]() $\unicode[STIX]{x1D716}$
-degree
$\unicode[STIX]{x1D716}$
-degree
![]() $k$
. Let
$k$
. Let
![]() $A_{k}^{j}=A^{j}\cap A_{k}$
. Note that we have
$A_{k}^{j}=A^{j}\cap A_{k}$
. Note that we have
whereas
![]() $\unicode[STIX]{x1D6E4}_{a}$
preserves both
$\unicode[STIX]{x1D6E4}_{a}$
preserves both
![]() $d$
-and
$d$
-and
![]() $\unicode[STIX]{x1D716}$
-degree. It follows immediately that
$\unicode[STIX]{x1D716}$
-degree. It follows immediately that
![]() $R$
is also
$R$
is also
![]() $d$
-graded. Thus the Hilbert series of
$d$
-graded. Thus the Hilbert series of
![]() $R$
(with respect to
$R$
(with respect to
![]() $d$
) is
$d$
) is
Observe also that the Poisson bracket on
![]() $A$
is
$A$
is
![]() $d$
-homogeneous:
$d$
-homogeneous:
![]() $\{A_{k},A_{\ell }\}\subseteq A_{k+\ell }$
.
$\{A_{k},A_{\ell }\}\subseteq A_{k+\ell }$
.
On the other hand,
![]() $\unicode[STIX]{x1D716}$
defines a filtration on
$\unicode[STIX]{x1D716}$
defines a filtration on
![]() $R$
:
$R$
:
Lemma 3.5. Let
![]() $A=A(n,a)$
with Poisson bracket
$A=A(n,a)$
with Poisson bracket
![]() $\{-,-\}$
and let
$\{-,-\}$
and let
![]() $R=R(n,a)$
, with multiplication
$R=R(n,a)$
, with multiplication
![]() $\ast$
. Let
$\ast$
. Let
![]() $R^{{\leqslant}k}:=\bigoplus _{\ell \leqslant k}A^{\ell }$
, considered as a subspace of
$R^{{\leqslant}k}:=\bigoplus _{\ell \leqslant k}A^{\ell }$
, considered as a subspace of
![]() $R$
. Then
$R$
. Then
![]() $R^{{\leqslant}k}\ast R^{{\leqslant}\ell }\subseteq R^{{\leqslant}k+\ell }$
, so
$R^{{\leqslant}k}\ast R^{{\leqslant}\ell }\subseteq R^{{\leqslant}k+\ell }$
, so
![]() $R$
is filtered by the
$R$
is filtered by the
![]() $R^{{\leqslant}k}$
. The associated graded algebra of
$R^{{\leqslant}k}$
. The associated graded algebra of
![]() $R$
is naturally isomorphic as a graded algebra to
$R$
is naturally isomorphic as a graded algebra to
![]() $A$
, and under this identification we have
$A$
, and under this identification we have
Proof. As graded vector spaces, since
![]() $R=A$
certainly
$R=A$
certainly
![]() $\operatorname{gr}R=\bigoplus _{k}R^{{\leqslant}k}/R^{{\leqslant}k-1}\cong \bigoplus _{k}A^{k}=A$
. Let
$\operatorname{gr}R=\bigoplus _{k}R^{{\leqslant}k}/R^{{\leqslant}k-1}\cong \bigoplus _{k}A^{k}=A$
. Let
![]() $f=\sum _{i=0}^{k}f_{i},g=\sum _{i=0}^{\ell }g_{i}\in A$
, where
$f=\sum _{i=0}^{k}f_{i},g=\sum _{i=0}^{\ell }g_{i}\in A$
, where
![]() $f_{i},g_{i}\in A^{i}$
and
$f_{i},g_{i}\in A^{i}$
and
![]() $f_{k},g_{\ell }\neq 0$
. From (2.3) and (3.3) we have that the
$f_{k},g_{\ell }\neq 0$
. From (2.3) and (3.3) we have that the
![]() $\unicode[STIX]{x1D716}$
-degree
$\unicode[STIX]{x1D716}$
-degree
![]() $k+\ell$
components of both
$k+\ell$
components of both
![]() $f\ast g$
and
$f\ast g$
and
![]() $g\ast f$
are equal to
$g\ast f$
are equal to
![]() $f_{k}g_{\ell }=g_{\ell }f_{k}$
so the multiplications on
$f_{k}g_{\ell }=g_{\ell }f_{k}$
so the multiplications on
![]() $\operatorname{gr}R$
and
$\operatorname{gr}R$
and
![]() $A$
agree.
$A$
agree.
Finally,
![]() $\operatorname{gr}(f\ast g-g\ast f)$
lies in
$\operatorname{gr}(f\ast g-g\ast f)$
lies in
![]() $\unicode[STIX]{x1D716}$
-degree
$\unicode[STIX]{x1D716}$
-degree
![]() $k+\ell -1$
and is thus equal to
$k+\ell -1$
and is thus equal to
as needed. ◻
Recall that a
![]() $\Bbbk$
-algebra
$\Bbbk$
-algebra
![]() $R$
is strongly Noetherian if
$R$
is strongly Noetherian if
![]() $R\otimes _{\Bbbk }C$
is Noetherian for any commutative Noetherian
$R\otimes _{\Bbbk }C$
is Noetherian for any commutative Noetherian
![]() $\Bbbk$
-algebra
$\Bbbk$
-algebra
![]() $C$
. (For example, polynomial rings are strongly Noetherian.) We have:
$C$
. (For example, polynomial rings are strongly Noetherian.) We have:
Corollary 3.6. For any
![]() $n\in \mathbb{Z}_{{>}0}$
and
$n\in \mathbb{Z}_{{>}0}$
and
![]() $a\in \Bbbk$
, the ring
$a\in \Bbbk$
, the ring
![]() $R(n,a)$
is a strongly Noetherian domain.
$R(n,a)$
is a strongly Noetherian domain.
Proof. This follows by standard arguments (see [Reference McConnell and RobsonMR01, Proposition 1.6.6, Theorem 1.6.9]) from the corresponding properties for
![]() $A(n,a)=\operatorname{gr}R(n,a)$
.◻
$A(n,a)=\operatorname{gr}R(n,a)$
.◻
The next result is useful because it allows us to use inductive arguments to establish properties of the
![]() $R(n,a)$
or
$R(n,a)$
or
![]() $A(n,a)$
.
$A(n,a)$
.
Proposition 3.7. Suppose that
![]() $n\geqslant 1$
. Let
$n\geqslant 1$
. Let
![]() $A=A(n,a)$
and let
$A=A(n,a)$
and let
![]() $R=R(n,a)$
. Then
$R=R(n,a)$
. Then
(1)
 $X_{0}$
is normal in
$X_{0}$
is normal in
 $R$
, and
$R$
, and
 $R/\langle X_{0}\rangle \cong R(n-1,a+1)$
.
$R/\langle X_{0}\rangle \cong R(n-1,a+1)$
.(2)
 $X_{0}$
is Poisson normal in
$X_{0}$
is Poisson normal in
 $A$
, and
$A$
, and
 $A/\langle X_{0}\rangle$
is Poisson isomorphic to
$A/\langle X_{0}\rangle$
is Poisson isomorphic to
 $A(n-1,a+1)$
.
$A(n-1,a+1)$
.
Proof.
![]() $(1)$
That
$(1)$
That
![]() $X_{0}\ast R=R\ast X_{0}=X_{0}A$
is immediate from (3.1), and so
$X_{0}\ast R=R\ast X_{0}=X_{0}A$
is immediate from (3.1), and so
![]() $X_{0}$
is normal.
$X_{0}$
is normal.
Let
![]() $\unicode[STIX]{x1D70B}:R\rightarrow R/\langle X_{0}\rangle$
be the canonical map, and let
$\unicode[STIX]{x1D70B}:R\rightarrow R/\langle X_{0}\rangle$
be the canonical map, and let
![]() $Y_{i}:=\unicode[STIX]{x1D70B}(X_{i+1})$
for all
$Y_{i}:=\unicode[STIX]{x1D70B}(X_{i+1})$
for all
![]() $0\leqslant i<n$
. Clearly
$0\leqslant i<n$
. Clearly
![]() $R/\langle X_{0}\rangle =R/X_{0}\ast R$
may be identified with
$R/\langle X_{0}\rangle =R/X_{0}\ast R$
may be identified with
![]() $A/X_{0}A=A/\langle X_{0}\rangle$
as a graded vector space, and this and
$A/X_{0}A=A/\langle X_{0}\rangle$
as a graded vector space, and this and
![]() $R(n-1,a+1)$
are isomorphic as graded vector spaces. From (3.1), the multiplication
$R(n-1,a+1)$
are isomorphic as graded vector spaces. From (3.1), the multiplication
![]() $\ast$
on
$\ast$
on
![]() $R/\langle X_{0}\rangle$
satisfies
$R/\langle X_{0}\rangle$
satisfies
which is precisely the multiplication on
![]() $R(n-1,a+1)$
.
$R(n-1,a+1)$
.
Note that the isomorphism
![]() $R/\langle X_{0}\rangle \cong R(n-1,a+1)$
respects both the
$R/\langle X_{0}\rangle \cong R(n-1,a+1)$
respects both the
![]() $d$
-grading and the
$d$
-grading and the
![]() $\unicode[STIX]{x1D716}$
-filtration on
$\unicode[STIX]{x1D716}$
-filtration on
![]() $R$
.
$R$
.
For
![]() $(2)$
, it is clear that
$(2)$
, it is clear that
![]() $X_{0}$
is Poisson normal. Since
$X_{0}$
is Poisson normal. Since
![]() $A/\langle X_{0}\rangle$
is the associated graded of the
$A/\langle X_{0}\rangle$
is the associated graded of the
![]() $\unicode[STIX]{x1D716}$
-filtration on
$\unicode[STIX]{x1D716}$
-filtration on
![]() $R/\langle X_{0}\rangle \cong R(n-1,a+1)$
, the remaining statement follows immediately from Lemma 3.5.◻
$R/\langle X_{0}\rangle \cong R(n-1,a+1)$
, the remaining statement follows immediately from Lemma 3.5.◻
We next prove that the algebras
![]() $R(n,a)$
have good homological properties. Recall that an
$R(n,a)$
have good homological properties. Recall that an
![]() $\mathbb{N}$
-graded
$\mathbb{N}$
-graded
![]() $\Bbbk$
-algebra
$\Bbbk$
-algebra
![]() $R$
with
$R$
with
![]() $R_{0}=\Bbbk$
is Artin–Schelter regular or AS-regular if:
$R_{0}=\Bbbk$
is Artin–Schelter regular or AS-regular if:
(1)
 $\operatorname{gldim}R<\infty$
;
$\operatorname{gldim}R<\infty$
;(2)
 $R$
has finite Gelfand–Kirillov dimension;
$R$
has finite Gelfand–Kirillov dimension;(3)
 $\operatorname{Ext}_{R}^{i}(\Bbbk _{R},R_{R})\cong \left\{\begin{array}{@{}ll@{}}0\quad & \text{if }i\neq \operatorname{gldim}R\\ \text{}_{R}\Bbbk [\ell ]\quad & \text{if }i=\operatorname{gldim}R.\end{array}\right.$
$\operatorname{Ext}_{R}^{i}(\Bbbk _{R},R_{R})\cong \left\{\begin{array}{@{}ll@{}}0\quad & \text{if }i\neq \operatorname{gldim}R\\ \text{}_{R}\Bbbk [\ell ]\quad & \text{if }i=\operatorname{gldim}R.\end{array}\right.$
(Here
![]() $\Bbbk [\ell ]$
means that the module is degree-shifted by some amount
$\Bbbk [\ell ]$
means that the module is degree-shifted by some amount
![]() $\ell \in \mathbb{Z}$
.) The Artin–Schelter regular condition is a noncommutative analogue of the good properties of commutative polynomial rings [Reference Artin and SchelterAS87]. Condition (3) above is called the AS–Gorenstein condition.
$\ell \in \mathbb{Z}$
.) The Artin–Schelter regular condition is a noncommutative analogue of the good properties of commutative polynomial rings [Reference Artin and SchelterAS87]. Condition (3) above is called the AS–Gorenstein condition.
Theorem 3.8. Fix
![]() $n\in \mathbb{Z}_{{>}0}$
and let
$n\in \mathbb{Z}_{{>}0}$
and let
![]() $a\in \Bbbk$
. The algebra
$a\in \Bbbk$
. The algebra
![]() $R=R(n,a)$
is Artin–Schelter regular of global dimension
$R=R(n,a)$
is Artin–Schelter regular of global dimension
![]() $n+1$
.
$n+1$
.
Proof. We prove by induction on
![]() $n$
that
$n$
that
![]() $R$
is AS-regular, Auslander–Gorenstein, and Cohen–Macaulay. We do not give the definitions of Auslander–Gorenstein or Cohen–Macaulay; the unfamiliar reader may treat them as technical terms internal to this proof.
$R$
is AS-regular, Auslander–Gorenstein, and Cohen–Macaulay. We do not give the definitions of Auslander–Gorenstein or Cohen–Macaulay; the unfamiliar reader may treat them as technical terms internal to this proof.
It is well known that the Jordan plane
![]() $R(1,a)$
and the polynomial ring
$R(1,a)$
and the polynomial ring
![]() $R(1,0)$
satisfy all of the above properties, so that the base case
$R(1,0)$
satisfy all of the above properties, so that the base case
![]() $n=1$
is clear. Thus we may assume that
$n=1$
is clear. Thus we may assume that
![]() $n>1$
.
$n>1$
.
By Lemma 3.5
![]() $A(n,a)$
is the associated graded ring of
$A(n,a)$
is the associated graded ring of
![]() $R$
under the
$R$
under the
![]() $\unicode[STIX]{x1D716}$
-filtration. Thus by [Reference McConnell and RobsonMR01, Corollary 7.6.18],
$\unicode[STIX]{x1D716}$
-filtration. Thus by [Reference McConnell and RobsonMR01, Corollary 7.6.18],
![]() $\operatorname{gldim}R\leqslant \operatorname{gldim}A(n,a)=n+1$
. By Proposition 3.7 and [Reference McConnell and RobsonMR01, Theorem 7.3.5],
$\operatorname{gldim}R\leqslant \operatorname{gldim}A(n,a)=n+1$
. By Proposition 3.7 and [Reference McConnell and RobsonMR01, Theorem 7.3.5],
![]() $\operatorname{gldim}R\geqslant \operatorname{gldim}R(n-1,a+1)+1$
. This last is
$\operatorname{gldim}R\geqslant \operatorname{gldim}R(n-1,a+1)+1$
. This last is
![]() $n$
by induction. Thus
$n$
by induction. Thus
![]() $\operatorname{gldim}R=n+1$
.
$\operatorname{gldim}R=n+1$
.
By induction,
![]() $R(n-1,a+1)$
is Auslander–Gorenstein and Cohen–Macaulay. By [Reference LevasseurLev92, Theorem 5.10], the same holds for
$R(n-1,a+1)$
is Auslander–Gorenstein and Cohen–Macaulay. By [Reference LevasseurLev92, Theorem 5.10], the same holds for
![]() $R$
. By [Reference LevasseurLev92, Theorem 6.3] and (3.4),
$R$
. By [Reference LevasseurLev92, Theorem 6.3] and (3.4),
![]() $R$
is AS–Gorenstein and thus AS-regular.◻
$R$
is AS–Gorenstein and thus AS-regular.◻
We now compute the relations for
![]() $R$
. We use the Vandermonde identity: for all
$R$
. We use the Vandermonde identity: for all
![]() $a,b\in \Bbbk$
and
$a,b\in \Bbbk$
and
![]() $k\in \mathbb{N}$
, we have
$k\in \mathbb{N}$
, we have
We also use the following lemma:
Lemma 3.10. Let
![]() $V=A_{1}=\operatorname{span}_{\Bbbk }(X_{0},\ldots ,X_{n})$
. For
$V=A_{1}=\operatorname{span}_{\Bbbk }(X_{0},\ldots ,X_{n})$
. For
![]() $b\in \Bbbk$
, define a linear map
$b\in \Bbbk$
, define a linear map
![]() $\unicode[STIX]{x1D719}_{b}:V\rightarrow V$
by
$\unicode[STIX]{x1D719}_{b}:V\rightarrow V$
by
Then
![]() $\unicode[STIX]{x1D719}_{a}\unicode[STIX]{x1D719}_{b}=\unicode[STIX]{x1D719}_{a+b}$
.
$\unicode[STIX]{x1D719}_{a}\unicode[STIX]{x1D719}_{b}=\unicode[STIX]{x1D719}_{a+b}$
.
Proof. By (3.9) we have:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{a}\unicode[STIX]{x1D719}_{b}(X_{j}) & = & \displaystyle \unicode[STIX]{x1D719}_{a}\left(\mathop{\sum }_{i=0}^{j}\binom{b}{i}X_{j-i}\right)=\mathop{\sum }_{i=0}^{j}\binom{b}{i}\left(\mathop{\sum }_{\ell =0}^{j-i}\binom{a}{\ell }X_{j-i-\ell }\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{j}\left(\mathop{\sum }_{u=0}^{k}\binom{b}{u}\binom{a}{k-u}\!\right)X_{j-k}=\mathop{\sum }_{k=0}^{j}\binom{a+b}{k}X_{j-k}=\unicode[STIX]{x1D719}_{a+b}(X_{j}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{a}\unicode[STIX]{x1D719}_{b}(X_{j}) & = & \displaystyle \unicode[STIX]{x1D719}_{a}\left(\mathop{\sum }_{i=0}^{j}\binom{b}{i}X_{j-i}\right)=\mathop{\sum }_{i=0}^{j}\binom{b}{i}\left(\mathop{\sum }_{\ell =0}^{j-i}\binom{a}{\ell }X_{j-i-\ell }\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=0}^{j}\left(\mathop{\sum }_{u=0}^{k}\binom{b}{u}\binom{a}{k-u}\!\right)X_{j-k}=\mathop{\sum }_{k=0}^{j}\binom{a+b}{k}X_{j-k}=\unicode[STIX]{x1D719}_{a+b}(X_{j}).\nonumber\end{eqnarray}$$
◻
The following lemma gives us quadratic relations that are satisfied in
![]() $R$
. We also give an equation that reverses the deformation formula (3.1) and thus allows us to obtain the commutative product from the noncommutative product
$R$
. We also give an equation that reverses the deformation formula (3.1) and thus allows us to obtain the commutative product from the noncommutative product
![]() $\ast$
.
$\ast$
.
Recall that we set
![]() $z_{j}=a+j$
.
$z_{j}=a+j$
.
Lemma 3.11. For all
![]() $0\leqslant i,j\leqslant n$
we have
$0\leqslant i,j\leqslant n$
we have
and
Proof. Fix
![]() $j$
, and recall the definition of the linear map
$j$
, and recall the definition of the linear map
![]() $\unicode[STIX]{x1D719}_{b}$
from Lemma 3.10. Since for any
$\unicode[STIX]{x1D719}_{b}$
from Lemma 3.10. Since for any
![]() $F\in R_{1}$
we have
$F\in R_{1}$
we have
![]() $F\ast X_{j}=\unicode[STIX]{x1D719}_{z_{j}}(F)X_{j}$
, clearly
$F\ast X_{j}=\unicode[STIX]{x1D719}_{z_{j}}(F)X_{j}$
, clearly
![]() $X_{i}X_{j}=\unicode[STIX]{x1D719}_{z_{j}}^{-1}(X_{i})\ast X_{j}$
. By Lemma 3.10, we immediately obtain (3.12).
$X_{i}X_{j}=\unicode[STIX]{x1D719}_{z_{j}}^{-1}(X_{i})\ast X_{j}$
. By Lemma 3.10, we immediately obtain (3.12).
Applying (3.12) to the equation
![]() $X_{i}X_{j}=X_{j}X_{i}$
, we obtain (3.13).◻
$X_{i}X_{j}=X_{j}X_{i}$
, we obtain (3.13).◻
Note that relations (3.13) can be rewritten as:
We now have:
Proposition 3.15. The relations in
![]() $R=R(n,a)$
are exactly the
$R=R(n,a)$
are exactly the
![]() $\binom{n+1}{2}$
relations given by (3.13) for
$\binom{n+1}{2}$
relations given by (3.13) for
![]() $0\leqslant i<j\leqslant n$
.
$0\leqslant i<j\leqslant n$
.
Proof. By comparing
![]() $\dim R_{1}\otimes _{\Bbbk }R_{1}$
and
$\dim R_{1}\otimes _{\Bbbk }R_{1}$
and
![]() $\dim R_{2}$
it is clear that
$\dim R_{2}$
it is clear that
![]() $R$
satisfies
$R$
satisfies
![]() $\binom{n+1}{2}$
quadratic relations; since the relations in (3.13) are linearly independent for
$\binom{n+1}{2}$
quadratic relations; since the relations in (3.13) are linearly independent for
![]() $0\leqslant i<j\leqslant n$
they are precisely the quadratic relations of
$0\leqslant i<j\leqslant n$
they are precisely the quadratic relations of
![]() $R$
.
$R$
.
By Theorem 3.8
![]() $R$
is AS-regular, and by (3.4) it is what is referred to as a quantum
$R$
is AS-regular, and by (3.4) it is what is referred to as a quantum
![]() $\mathbb{P}^{n}$
in [Reference Shelton and TingeyST01]. Thus by [Reference Shelton and TingeyST01, Theorem 2.2],
$\mathbb{P}^{n}$
in [Reference Shelton and TingeyST01]. Thus by [Reference Shelton and TingeyST01, Theorem 2.2],
![]() $R$
is Koszul and in particular is given by quadratic relations. Thus the relations in (3.13) are precisely the relations of
$R$
is Koszul and in particular is given by quadratic relations. Thus the relations in (3.13) are precisely the relations of
![]() $R$
.◻
$R$
.◻
Example 3.16. When
![]() $n=1$
we obtain:
$n=1$
we obtain:
For
![]() $a\neq 0$
the algebra
$a\neq 0$
the algebra
![]() $R(1,a)$
is isomorphic to the well-known Jordan plane, and the Poisson algebra
$R(1,a)$
is isomorphic to the well-known Jordan plane, and the Poisson algebra
![]() $A(1,a)$
is isomorphic to the Poisson–Jordan plane: the polynomial algebra
$A(1,a)$
is isomorphic to the Poisson–Jordan plane: the polynomial algebra
![]() $\Bbbk [X_{0},X_{1}]$
endowed with Poisson bracket
$\Bbbk [X_{0},X_{1}]$
endowed with Poisson bracket
![]() $\{X_{0},X_{1}\}=X_{0}^{2}$
.
$\{X_{0},X_{1}\}=X_{0}^{2}$
.
Example 3.17. When
![]() $n=2$
the algebra
$n=2$
the algebra
![]() $R(2,a)$
is given by generators
$R(2,a)$
is given by generators
![]() $X_{0},X_{1},X_{2}$
and relations:
$X_{0},X_{1},X_{2}$
and relations:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}X_{0}\ast X_{1}-X_{1}\ast X_{0}\ & =\ & \displaystyle -aX_{0}\ast X_{0},\\ X_{0}\ast X_{2}-X_{2}\ast X_{0}\ & =\ & \displaystyle -aX_{0}\ast X_{1}-\binom{a}{2}X_{0}\ast X_{0},\\ X_{1}\ast X_{2}-X_{2}\ast X_{1}\ & =\ & \displaystyle (a+2)X_{0}\ast X_{2}-(a+1)X_{1}\ast X_{1}\\ \ & \ & \displaystyle +\,\binom{a+2}{2}X_{0}\ast X_{1}.\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}X_{0}\ast X_{1}-X_{1}\ast X_{0}\ & =\ & \displaystyle -aX_{0}\ast X_{0},\\ X_{0}\ast X_{2}-X_{2}\ast X_{0}\ & =\ & \displaystyle -aX_{0}\ast X_{1}-\binom{a}{2}X_{0}\ast X_{0},\\ X_{1}\ast X_{2}-X_{2}\ast X_{1}\ & =\ & \displaystyle (a+2)X_{0}\ast X_{2}-(a+1)X_{1}\ast X_{1}\\ \ & \ & \displaystyle +\,\binom{a+2}{2}X_{0}\ast X_{1}.\end{array} & & \displaystyle\end{eqnarray}$$
The Poisson bracket on
![]() $A(2,a)$
is given by:
$A(2,a)$
is given by:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}\{X_{0},X_{1}\}\ & =\ & -aX_{0}^{2},\\ \{X_{0},X_{2}\}\ & =\ & -aX_{0}X_{1},\\ \{X_{1},X_{2}\}\ & =\ & (a+2)X_{0}X_{2}-(a+1)X_{1}^{2}.\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}\{X_{0},X_{1}\}\ & =\ & -aX_{0}^{2},\\ \{X_{0},X_{2}\}\ & =\ & -aX_{0}X_{1},\\ \{X_{1},X_{2}\}\ & =\ & (a+2)X_{0}X_{2}-(a+1)X_{1}^{2}.\end{array} & & \displaystyle\end{eqnarray}$$
Example 3.20. When
![]() $n=3$
and
$n=3$
and
![]() $a=-5/4$
we obtain an algebra isomorphic to Pym’s example (1.1). The isomorphism sends
$a=-5/4$
we obtain an algebra isomorphic to Pym’s example (1.1). The isomorphism sends
![]() $X_{i}\mapsto x_{i}/4^{i}$
for
$X_{i}\mapsto x_{i}/4^{i}$
for
![]() $i=0,\ldots ,3$
.
$i=0,\ldots ,3$
.
We now prove a technical result which gives equivalent conditions for an element to be normal (or Poisson normal), under mild conditions on
![]() $a$
and
$a$
and
![]() $n$
. In particular we show that, up to multiplication by nonzero scalars,
$n$
. In particular we show that, up to multiplication by nonzero scalars,
![]() $X_{0}$
is the only homogeneous element of
$X_{0}$
is the only homogeneous element of
![]() $d$
-degree
$d$
-degree
![]() $1$
that is (Poisson) normal.
$1$
that is (Poisson) normal.
Proposition 3.21. Assume either that
![]() $n\geqslant 2$
or that
$n\geqslant 2$
or that
![]() $n=1$
and
$n=1$
and
![]() $a\neq 0$
. Then:
$a\neq 0$
. Then:
(1a)
![]() $N$
is Poisson normal in
$N$
is Poisson normal in
![]() $A=A(n,a)$
$A=A(n,a)$
![]() $\;\Longleftrightarrow \;$
(1b)
$\;\Longleftrightarrow \;$
(1b)
![]() $N$
is normal in
$N$
is normal in
![]() $R=R(n,a)$
$R=R(n,a)$
![]() $\;\Longleftrightarrow \;$
(1c) we have
$\;\Longleftrightarrow \;$
(1c) we have
![]() $\unicode[STIX]{x1D6E5}(N)=0$
and
$\unicode[STIX]{x1D6E5}(N)=0$
and
![]() $\unicode[STIX]{x1D6E4}_{a}(N)=uN$
for some
$\unicode[STIX]{x1D6E4}_{a}(N)=uN$
for some
![]() $u\in \Bbbk$
.
$u\in \Bbbk$
.
(2a)
![]() $N$
is Poisson central in
$N$
is Poisson central in
![]() $A$
$A$
![]() $\;\Longleftrightarrow \;$
(2b)
$\;\Longleftrightarrow \;$
(2b)
![]() $N$
is central in
$N$
is central in
![]() $R$
$R$
![]() $\;\Longleftrightarrow \;$
(2c) we have
$\;\Longleftrightarrow \;$
(2c) we have
![]() $\unicode[STIX]{x1D6E5}(N)=\unicode[STIX]{x1D6E4}_{a}(N)=0$
.
$\unicode[STIX]{x1D6E5}(N)=\unicode[STIX]{x1D6E4}_{a}(N)=0$
.
Proof. Without loss of generality,
![]() $n>0$
. The implications
$n>0$
. The implications
![]() $(1c)\Rightarrow (1a),(1b)$
and
$(1c)\Rightarrow (1a),(1b)$
and
![]() $(2c)\Rightarrow (2a),(2b)$
are clear from (2.3). To prove the other implications, we first prove:
$(2c)\Rightarrow (2a),(2b)$
are clear from (2.3). To prove the other implications, we first prove:
Claim. There is an irreducible
![]() $G\in A$
with
$G\in A$
with
![]() $\unicode[STIX]{x1D6E5}(G)=0$
and
$\unicode[STIX]{x1D6E5}(G)=0$
and
![]() $\unicode[STIX]{x1D6E4}(G)=\unicode[STIX]{x1D706}G$
for some
$\unicode[STIX]{x1D6E4}(G)=\unicode[STIX]{x1D706}G$
for some
![]() $\unicode[STIX]{x1D706}\neq 0$
, and further such that
$\unicode[STIX]{x1D706}\neq 0$
, and further such that
![]() $\langle G\rangle =G\ast R=R\ast G$
is a completely prime ideal of
$\langle G\rangle =G\ast R=R\ast G$
is a completely prime ideal of
![]() $R$
.
$R$
.
To prove the claim, if
![]() $a\neq 0$
then we may take
$a\neq 0$
then we may take
![]() $G=X_{0}$
, so
$G=X_{0}$
, so
![]() $\unicode[STIX]{x1D706}=a$
. The last statement follows from the isomorphism
$\unicode[STIX]{x1D706}=a$
. The last statement follows from the isomorphism
![]() $R/\langle X_{0}\rangle \cong R(n-1,a+1)$
.
$R/\langle X_{0}\rangle \cong R(n-1,a+1)$
.
If
![]() $a=0$
and
$a=0$
and
![]() $n\geqslant 2$
then let
$n\geqslant 2$
then let
![]() $G=X_{0}X_{2}-\frac{1}{2}X_{1}^{2}$
and
$G=X_{0}X_{2}-\frac{1}{2}X_{1}^{2}$
and
![]() $\unicode[STIX]{x1D706}=2$
. We have
$\unicode[STIX]{x1D706}=2$
. We have
![]() $\unicode[STIX]{x1D6E5}(G)=0$
and
$\unicode[STIX]{x1D6E5}(G)=0$
and
![]() $\unicode[STIX]{x1D6E4}_{a}(G)=2(a+1)G=\unicode[STIX]{x1D706}G$
. Note that
$\unicode[STIX]{x1D6E4}_{a}(G)=2(a+1)G=\unicode[STIX]{x1D706}G$
. Note that
![]() $G$
is normal in
$G$
is normal in
![]() $R$
and
$R$
and
![]() $\unicode[STIX]{x1D716}$
-homogeneous and so the
$\unicode[STIX]{x1D716}$
-homogeneous and so the
![]() $\unicode[STIX]{x1D716}$
-filtration on
$\unicode[STIX]{x1D716}$
-filtration on
![]() $R$
descends to
$R$
descends to
![]() $R/\langle G\rangle$
. It is clear that
$R/\langle G\rangle$
. It is clear that
![]() $\operatorname{gr}(R/\langle G\rangle )$
is isomorphic to
$\operatorname{gr}(R/\langle G\rangle )$
is isomorphic to
![]() $A/\langle G\rangle$
which is a domain, so
$A/\langle G\rangle$
which is a domain, so
![]() $G\ast R$
is completely prime.
$G\ast R$
is completely prime.
We now prove
![]() $(1a)\Rightarrow (1c)$
. Let
$(1a)\Rightarrow (1c)$
. Let
![]() $G,\unicode[STIX]{x1D706}$
be as in the Claim. Suppose that
$G,\unicode[STIX]{x1D706}$
be as in the Claim. Suppose that
![]() $N$
is Poisson normal in
$N$
is Poisson normal in
![]() $A$
. Without loss of generality we can assume that
$A$
. Without loss of generality we can assume that
![]() $N\notin GA$
and
$N\notin GA$
and
![]() $N\not \in X_{0}A$
since
$N\not \in X_{0}A$
since
![]() $G$
and
$G$
and
![]() $X_{0}$
are Poisson normal. Because
$X_{0}$
are Poisson normal. Because
![]() $\{G,N\}=-\unicode[STIX]{x1D706}G\unicode[STIX]{x1D6E5}(N)\in NA$
, there exists
$\{G,N\}=-\unicode[STIX]{x1D706}G\unicode[STIX]{x1D6E5}(N)\in NA$
, there exists
![]() $G^{\prime }\in A$
such that
$G^{\prime }\in A$
such that
![]() $G\unicode[STIX]{x1D6E5}(N)=G^{\prime }N$
. Since
$G\unicode[STIX]{x1D6E5}(N)=G^{\prime }N$
. Since
![]() $N\notin GA$
and
$N\notin GA$
and
![]() $G$
is irreducible there exists
$G$
is irreducible there exists
![]() $v\in A$
such that
$v\in A$
such that
![]() $G^{\prime }=vG$
and we obtain
$G^{\prime }=vG$
and we obtain
![]() $\unicode[STIX]{x1D6E5}(N)=vN$
after dividing by
$\unicode[STIX]{x1D6E5}(N)=vN$
after dividing by
![]() $G$
. Since
$G$
. Since
![]() $\unicode[STIX]{x1D6E5}$
is
$\unicode[STIX]{x1D6E5}$
is
![]() $d$
-homogeneous we must have
$d$
-homogeneous we must have
![]() $v\in A_{0}=\Bbbk$
. But
$v\in A_{0}=\Bbbk$
. But
![]() $\unicode[STIX]{x1D6E5}$
is locally nilpotent so we must have
$\unicode[STIX]{x1D6E5}$
is locally nilpotent so we must have
![]() $v=0$
and
$v=0$
and
![]() $\unicode[STIX]{x1D6E5}(N)=0$
.
$\unicode[STIX]{x1D6E5}(N)=0$
.
There therefore exists
![]() $X_{1}^{\prime }\in A$
such that:
$X_{1}^{\prime }\in A$
such that:
Again since
![]() $N\notin X_{0}A$
we can write
$N\notin X_{0}A$
we can write
![]() $X_{1}^{\prime }=X_{0}u$
for some
$X_{1}^{\prime }=X_{0}u$
for some
![]() $u\in A$
, and we have
$u\in A$
, and we have
![]() $\unicode[STIX]{x1D6E4}_{a}(N)=uN$
. The derivation
$\unicode[STIX]{x1D6E4}_{a}(N)=uN$
. The derivation
![]() $\unicode[STIX]{x1D6E4}_{a}$
being
$\unicode[STIX]{x1D6E4}_{a}$
being
![]() $d$
-homogeneous, we conclude as before that
$d$
-homogeneous, we conclude as before that
![]() $u\in A_{0}=\Bbbk$
is a scalar.
$u\in A_{0}=\Bbbk$
is a scalar.
We now prove
![]() $(1b)\Rightarrow (1c)$
. Suppose that
$(1b)\Rightarrow (1c)$
. Suppose that
![]() $N$
is normal in
$N$
is normal in
![]() $R$
. Without loss of generality we can assume that
$R$
. Without loss of generality we can assume that
![]() $N\notin X_{0}\ast R$
and
$N\notin X_{0}\ast R$
and
![]() $N\not \in G\ast R$
since
$N\not \in G\ast R$
since
![]() $X_{0}$
and
$X_{0}$
and
![]() $G$
are normal. By normality of
$G$
are normal. By normality of
![]() $N$
there exists
$N$
there exists
![]() $G^{\prime }$
such that
$G^{\prime }$
such that
![]() $G\ast N=N\ast G^{\prime }$
. Since
$G\ast N=N\ast G^{\prime }$
. Since
![]() $N\notin G\ast R$
we must have
$N\notin G\ast R$
we must have
![]() $G^{\prime }\in G\ast R$
as
$G^{\prime }\in G\ast R$
as
![]() $G\ast R$
is completely prime. Moreover, using the equation
$G\ast R$
is completely prime. Moreover, using the equation
![]() $G\ast N=N\ast G^{\prime }$
we deduce that
$G\ast N=N\ast G^{\prime }$
we deduce that
![]() $G^{\prime }$
is
$G^{\prime }$
is
![]() $d$
-homogeneous and
$d$
-homogeneous and
![]() $d(G^{\prime })=d(G)$
. So
$d(G^{\prime })=d(G)$
. So
![]() $G^{\prime }=wG$
for a scalar
$G^{\prime }=wG$
for a scalar
![]() $w$
, and we conclude that
$w$
, and we conclude that
![]() $N$
must satisfy the equation
$N$
must satisfy the equation
![]() $G\ast N=wN\ast G$
. Using the definition of the product
$G\ast N=wN\ast G$
. Using the definition of the product
![]() $\ast$
we obtain the following equation after dividing by
$\ast$
we obtain the following equation after dividing by
![]() $G$
:
$G$
:
for some
![]() $k\geqslant 0$
. We decompose
$k\geqslant 0$
. We decompose
![]() $N=\sum _{i=0}^{\ell }N_{i}\in \bigoplus A^{i}$
into
$N=\sum _{i=0}^{\ell }N_{i}\in \bigoplus A^{i}$
into
![]() $\unicode[STIX]{x1D716}$
-homogeneous pieces. Since
$\unicode[STIX]{x1D716}$
-homogeneous pieces. Since
![]() $\unicode[STIX]{x1D6E5}(A^{i})\subseteq A^{i-1}$
we deduce from Equation (3.22) that
$\unicode[STIX]{x1D6E5}(A^{i})\subseteq A^{i-1}$
we deduce from Equation (3.22) that
![]() $N_{\ell }=wN_{\ell }$
, that is,
$N_{\ell }=wN_{\ell }$
, that is,
![]() $w=1$
and
$w=1$
and
![]() $\unicode[STIX]{x1D6E5}(N_{\ell })=0$
. Finally we obtain by (a decreasing) induction that
$\unicode[STIX]{x1D6E5}(N_{\ell })=0$
. Finally we obtain by (a decreasing) induction that
![]() $\unicode[STIX]{x1D6E5}(N_{i})=0$
for all
$\unicode[STIX]{x1D6E5}(N_{i})=0$
for all
![]() $i$
, so that
$i$
, so that
![]() $N\in \ker \unicode[STIX]{x1D6E5}$
.
$N\in \ker \unicode[STIX]{x1D6E5}$
.
By normality of
![]() $N$
there exists
$N$
there exists
![]() $F\in R$
such that
$F\in R$
such that
![]() $X_{1}\ast N=N\ast F$
. Since
$X_{1}\ast N=N\ast F$
. Since
![]() $\unicode[STIX]{x1D6E5}(N)=0$
we have
$\unicode[STIX]{x1D6E5}(N)=0$
we have
so
![]() $N$
divides
$N$
divides
![]() $X_{0}\unicode[STIX]{x1D6E4}_{a}(N)\in A$
. As
$X_{0}\unicode[STIX]{x1D6E4}_{a}(N)\in A$
. As
![]() $N\not \in X_{0}\ast R=X_{0}A$
we have that
$N\not \in X_{0}\ast R=X_{0}A$
we have that
![]() $N$
divides
$N$
divides
![]() $\unicode[STIX]{x1D6E4}_{a}(N)$
, so there exists
$\unicode[STIX]{x1D6E4}_{a}(N)$
, so there exists
![]() $u\in A$
with
$u\in A$
with
![]() $\unicode[STIX]{x1D6E4}_{a}(N)=uN$
. Comparing
$\unicode[STIX]{x1D6E4}_{a}(N)=uN$
. Comparing
![]() $d$
-degrees we have
$d$
-degrees we have
![]() $u\in A_{0}=\Bbbk$
.
$u\in A_{0}=\Bbbk$
.
For the remaining equivalences note that if
![]() $N$
is either Poisson central in
$N$
is either Poisson central in
![]() $A$
or central in
$A$
or central in
![]() $R$
then certainly
$R$
then certainly
![]() $N$
is (Poisson) normal. We have seen that
$N$
is (Poisson) normal. We have seen that
![]() $\unicode[STIX]{x1D6E5}(N)=0$
and
$\unicode[STIX]{x1D6E5}(N)=0$
and
![]() $\unicode[STIX]{x1D6E4}_{a}(N)=uN$
for some
$\unicode[STIX]{x1D6E4}_{a}(N)=uN$
for some
![]() $u\in \Bbbk$
. We then have either:
$u\in \Bbbk$
. We then have either:
![]() $0=\{X_{1},N\}=uX_{0}N$
(if
$0=\{X_{1},N\}=uX_{0}N$
(if
![]() $N$
is Poisson central) or
$N$
is Poisson central) or
![]() $0=X_{1}\ast N-N\ast X_{1}=uX_{0}N$
(if
$0=X_{1}\ast N-N\ast X_{1}=uX_{0}N$
(if
![]() $N$
is central). In either case
$N$
is central). In either case
![]() $u=0$
. Thus (2a)
$u=0$
. Thus (2a)
![]() $\Rightarrow$
(2c) and (2b)
$\Rightarrow$
(2c) and (2b)
![]() $\Rightarrow$
(2c).◻
$\Rightarrow$
(2c).◻
Remark 3.23. We note that Proposition 3.21 does not make it easy to find the normal (or central) elements of
![]() $R$
. In particular, it is a famously difficult problem in symbolic dynamics to calculate
$R$
. In particular, it is a famously difficult problem in symbolic dynamics to calculate
![]() $A^{\unicode[STIX]{x1D6E5}}=\{f\in A\mid \unicode[STIX]{x1D6E5}(f)=0\}$
; see [Reference FreudenburgFre13]. In fact,
$A^{\unicode[STIX]{x1D6E5}}=\{f\in A\mid \unicode[STIX]{x1D6E5}(f)=0\}$
; see [Reference FreudenburgFre13]. In fact,
![]() $A^{\unicode[STIX]{x1D6E5}}$
is not known explicitly for
$A^{\unicode[STIX]{x1D6E5}}$
is not known explicitly for
![]() $n\geqslant 9$
.
$n\geqslant 9$
.
The rings
![]() $R(n,a)$
are complicated to study but they become much simpler after localization at the normal element
$R(n,a)$
are complicated to study but they become much simpler after localization at the normal element
![]() $X_{0}$
. To end this section we study the localizations of
$X_{0}$
. To end this section we study the localizations of
![]() $R=R(n,a)$
and
$R=R(n,a)$
and
![]() $A=A(n,a)$
at the (Poisson) normal element
$A=A(n,a)$
at the (Poisson) normal element
![]() $X_{0}$
. Let
$X_{0}$
. Let
![]() $R^{\circ }:=R[X_{0}^{-1}]$
and
$R^{\circ }:=R[X_{0}^{-1}]$
and
![]() $A^{\circ }:=A[X_{0}^{-1}]$
. We note that
$A^{\circ }:=A[X_{0}^{-1}]$
. We note that
![]() $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
![]() $\unicode[STIX]{x1D6E4}_{a}$
extend to
$\unicode[STIX]{x1D6E4}_{a}$
extend to
![]() $A^{\circ }$
, and that the Poisson bracket
$A^{\circ }$
, and that the Poisson bracket
![]() $\{-,-\}_{a}$
extends to
$\{-,-\}_{a}$
extends to
![]() $A^{\circ }$
and is still defined by (2.4). Likewise, the multiplication
$A^{\circ }$
and is still defined by (2.4). Likewise, the multiplication
![]() $\ast _{a}$
on
$\ast _{a}$
on
![]() $R^{\circ }$
is still defined by (2.3). The
$R^{\circ }$
is still defined by (2.3). The
![]() $d$
-grading extends to
$d$
-grading extends to
![]() $A^{\circ }$
and to
$A^{\circ }$
and to
![]() $R^{\circ }$
. The
$R^{\circ }$
. The
![]() $\unicode[STIX]{x1D716}$
-grading extends to
$\unicode[STIX]{x1D716}$
-grading extends to
![]() $A^{\circ }$
, and
$A^{\circ }$
, and
![]() $\unicode[STIX]{x1D716}$
defines a filtration on
$\unicode[STIX]{x1D716}$
defines a filtration on
![]() $R^{\circ }$
with associated graded
$R^{\circ }$
with associated graded
![]() $A^{\circ }$
, as with the nonlocalized rings.
$A^{\circ }$
, as with the nonlocalized rings.
We further define a new grading
![]() $A^{\circ }=\bigoplus _{e\in \Bbbk }A^{\circ }(e)$
by defining
$A^{\circ }=\bigoplus _{e\in \Bbbk }A^{\circ }(e)$
by defining
![]() $A^{\circ }(e)$
to be the
$A^{\circ }(e)$
to be the
![]() $e$
-eigenspace of
$e$
-eigenspace of
![]() $\unicode[STIX]{x1D6E4}_{a}$
. Notice that
$\unicode[STIX]{x1D6E4}_{a}$
. Notice that
![]() $A^{\circ }(e)\neq 0$
if and only if
$A^{\circ }(e)\neq 0$
if and only if
![]() $e\in a\mathbb{Z}+\mathbb{N}$
. Further note that if
$e\in a\mathbb{Z}+\mathbb{N}$
. Further note that if
![]() $F\in (A^{\circ })_{d}^{\unicode[STIX]{x1D716}}$
, then
$F\in (A^{\circ })_{d}^{\unicode[STIX]{x1D716}}$
, then
![]() $F\in A^{\circ }(e)$
for
$F\in A^{\circ }(e)$
for
![]() $e=da+\unicode[STIX]{x1D716}$
. It follows from (3.3) that
$e=da+\unicode[STIX]{x1D716}$
. It follows from (3.3) that
![]() $A^{\circ }$
is also the associated graded ring of
$A^{\circ }$
is also the associated graded ring of
![]() $R^{\circ }$
with respect to the
$R^{\circ }$
with respect to the
![]() $e$
-filtration, and that the
$e$
-filtration, and that the
![]() $\unicode[STIX]{x1D716}$
- and
$\unicode[STIX]{x1D716}$
- and
![]() $e$
-filtrations on
$e$
-filtrations on
![]() $R^{\circ }$
both induce the Poisson bracket
$R^{\circ }$
both induce the Poisson bracket
![]() $\{-,-\}_{a}$
on
$\{-,-\}_{a}$
on
![]() $A^{\circ }$
.
$A^{\circ }$
.
Let
![]() $B=(A^{\circ })^{\unicode[STIX]{x1D6E5}}$
. In contrast to
$B=(A^{\circ })^{\unicode[STIX]{x1D6E5}}$
. In contrast to
![]() $A^{\unicode[STIX]{x1D6E5}}$
, which is unknown in general,
$A^{\unicode[STIX]{x1D6E5}}$
, which is unknown in general,
![]() $B$
is easy to compute and is isomorphic to a polynomial ring in
$B$
is easy to compute and is isomorphic to a polynomial ring in
![]() $n$
variables. Explicitly, for
$n$
variables. Explicitly, for
![]() $j\geqslant 1$
define
$j\geqslant 1$
define
This is well defined since
![]() $\unicode[STIX]{x1D6E5}$
is locally nilpotent. Note that
$\unicode[STIX]{x1D6E5}$
is locally nilpotent. Note that
![]() $Y_{j}\in (A^{\circ })_{1}^{j}$
; in particular,
$Y_{j}\in (A^{\circ })_{1}^{j}$
; in particular,
![]() $Y_{j}$
is
$Y_{j}$
is
![]() $e$
-homogeneous, with
$e$
-homogeneous, with
![]() $e(Y_{j})=e(X_{j})=z_{j}$
.
$e(Y_{j})=e(X_{j})=z_{j}$
.
Lemma 3.24. We have that
![]() $A^{\circ }$
is freely generated by
$A^{\circ }$
is freely generated by
![]() $X_{1},Y_{2},\ldots ,Y_{n}$
and
$X_{1},Y_{2},\ldots ,Y_{n}$
and
![]() $B$
is freely generated by
$B$
is freely generated by
![]() $Y_{2},\ldots ,Y_{n}$
as commutative algebras over
$Y_{2},\ldots ,Y_{n}$
as commutative algebras over
![]() $\Bbbk [X_{0}^{\pm 1}]$
.
$\Bbbk [X_{0}^{\pm 1}]$
.
Proof. That
![]() $B$
is generated by
$B$
is generated by
![]() $X_{0}^{\pm 1},Y_{2},\ldots ,Y_{n}$
follows from [Reference van den EssenvdE93, Proposition 2.1], since
$X_{0}^{\pm 1},Y_{2},\ldots ,Y_{n}$
follows from [Reference van den EssenvdE93, Proposition 2.1], since
![]() $\unicode[STIX]{x1D6E5}(X_{1}/X_{0})=1$
. If
$\unicode[STIX]{x1D6E5}(X_{1}/X_{0})=1$
. If
![]() $i\geqslant 2$
, then
$i\geqslant 2$
, then
This shows that the elements
![]() $X_{0},X_{1},Y_{2},\ldots ,Y_{n}$
are algebraically independent, proving that
$X_{0},X_{1},Y_{2},\ldots ,Y_{n}$
are algebraically independent, proving that
![]() $B$
is freely generated as claimed.
$B$
is freely generated as claimed.
By (3.25) and induction,
![]() $A^{\circ }$
is generated over
$A^{\circ }$
is generated over
![]() $B$
by
$B$
by
![]() $X_{1}$
, and thus over
$X_{1}$
, and thus over
![]() $\Bbbk [X_{0}^{\pm 1}]$
by
$\Bbbk [X_{0}^{\pm 1}]$
by
![]() $X_{1},Y_{2},\ldots ,Y_{n}$
. Since
$X_{1},Y_{2},\ldots ,Y_{n}$
. Since
![]() $\operatorname{Kdim}A^{\circ }=n+1$
, thus
$\operatorname{Kdim}A^{\circ }=n+1$
, thus
![]() $A^{\circ }$
is freely generated as well.◻
$A^{\circ }$
is freely generated as well.◻
Lemma 3.26. Let
![]() $\unicode[STIX]{x1D6FF}=X_{0}\unicode[STIX]{x1D6E4}_{a}$
, so
$\unicode[STIX]{x1D6FF}=X_{0}\unicode[STIX]{x1D6E4}_{a}$
, so
![]() $\unicode[STIX]{x1D6FF}\in \operatorname{Der}_{\Bbbk }(B)$
. Define a map
$\unicode[STIX]{x1D6FF}\in \operatorname{Der}_{\Bbbk }(B)$
. Define a map
![]() $\unicode[STIX]{x1D6FD}:B[z]\rightarrow A^{\circ }$
by
$\unicode[STIX]{x1D6FD}:B[z]\rightarrow A^{\circ }$
by
![]() $\unicode[STIX]{x1D6FD}(\sum b_{i}z^{i})=\sum b_{i}X_{1}^{i}$
. Then
$\unicode[STIX]{x1D6FD}(\sum b_{i}z^{i})=\sum b_{i}X_{1}^{i}$
. Then
![]() $\unicode[STIX]{x1D6FD}$
is a ring isomorphism
$\unicode[STIX]{x1D6FD}$
is a ring isomorphism
![]() $B[z;\unicode[STIX]{x1D6FF}]\rightarrow R^{\circ }$
and a Poisson isomorphism
$B[z;\unicode[STIX]{x1D6FF}]\rightarrow R^{\circ }$
and a Poisson isomorphism
![]() $(B[z],\{-.-\}_{\unicode[STIX]{x1D6FF}})\rightarrow A^{\circ }$
.
$(B[z],\{-.-\}_{\unicode[STIX]{x1D6FF}})\rightarrow A^{\circ }$
.
Proof. Since
![]() $B$
is an
$B$
is an
![]() $e$
-graded subring of
$e$
-graded subring of
![]() $A^{\circ }$
, therefore
$A^{\circ }$
, therefore
![]() $\unicode[STIX]{x1D6FF}(B)\subseteq B$
and so
$\unicode[STIX]{x1D6FF}(B)\subseteq B$
and so
![]() $\unicode[STIX]{x1D6FF}\in \operatorname{Der}_{\Bbbk }(B)$
.
$\unicode[STIX]{x1D6FF}\in \operatorname{Der}_{\Bbbk }(B)$
.
Let
![]() $\star$
be the multiplication in
$\star$
be the multiplication in
![]() $B[z;\unicode[STIX]{x1D6FF}]$
. Note that if we put
$B[z;\unicode[STIX]{x1D6FF}]$
. Note that if we put
![]() $e(z)=a+1$
then
$e(z)=a+1$
then
![]() $\unicode[STIX]{x1D6FD}$
is clearly
$\unicode[STIX]{x1D6FD}$
is clearly
![]() $e$
-graded as an isomorphism of vector spaces and
$e$
-graded as an isomorphism of vector spaces and
![]() $e$
-filtered as a map from
$e$
-filtered as a map from
![]() $B[z;\unicode[STIX]{x1D6FF}]\rightarrow R^{\circ }$
. Since
$B[z;\unicode[STIX]{x1D6FF}]\rightarrow R^{\circ }$
. Since
![]() $A^{\circ }$
is the associated graded of
$A^{\circ }$
is the associated graded of
![]() $R^{\circ }$
it suffices to prove that
$R^{\circ }$
it suffices to prove that
![]() $\unicode[STIX]{x1D6FD}:B[z;\unicode[STIX]{x1D6FF}]\rightarrow R^{\circ }$
is a ring homomorphism. It is enough to check that
$\unicode[STIX]{x1D6FD}:B[z;\unicode[STIX]{x1D6FF}]\rightarrow R^{\circ }$
is a ring homomorphism. It is enough to check that
![]() $\unicode[STIX]{x1D6FD}(z\star g)=\unicode[STIX]{x1D6FD}(z)\ast _{a}g$
for
$\unicode[STIX]{x1D6FD}(z\star g)=\unicode[STIX]{x1D6FD}(z)\ast _{a}g$
for
![]() $g\in B(e)$
. But we have
$g\in B(e)$
. But we have
as needed. ◻
4 Graded automorphisms and the Nakayama automorphism
In this section we compute the graded automorphism group of
![]() $R(n,a)$
and determine its Nakayama automorphism. In particular we prove Theorem 1.2.
$R(n,a)$
and determine its Nakayama automorphism. In particular we prove Theorem 1.2.
We begin with the graded automorphism group of
![]() $R(n,a)$
. In order to prove that the maps
$R(n,a)$
. In order to prove that the maps
![]() $\unicode[STIX]{x1D719}_{b}$
defined in Lemma 3.10 are well-defined automorphisms of
$\unicode[STIX]{x1D719}_{b}$
defined in Lemma 3.10 are well-defined automorphisms of
![]() $R(n,a)$
for any
$R(n,a)$
for any
![]() $a,b\in \Bbbk$
we use the theory of Zhang twists. More specifically we prove that
$a,b\in \Bbbk$
we use the theory of Zhang twists. More specifically we prove that
![]() $R(n,a)$
and
$R(n,a)$
and
![]() $R(n,b)$
are Zhang twists of each other for any
$R(n,b)$
are Zhang twists of each other for any
![]() $a,b\in \Bbbk$
. We now recall the definition of Zhang twist from [Reference ZhangZha96]. If
$a,b\in \Bbbk$
. We now recall the definition of Zhang twist from [Reference ZhangZha96]. If
![]() $S$
is an
$S$
is an
![]() $\mathbb{N}$
-graded ring with multiplication
$\mathbb{N}$
-graded ring with multiplication
![]() $\ast$
, and
$\ast$
, and
![]() $\unicode[STIX]{x1D719}\in \operatorname{Aut}(S)$
is a graded automorphism of
$\unicode[STIX]{x1D719}\in \operatorname{Aut}(S)$
is a graded automorphism of
![]() $S$
, then the Zhang twist of
$S$
, then the Zhang twist of
![]() $S$
by
$S$
by
![]() $\unicode[STIX]{x1D719}$
is written
$\unicode[STIX]{x1D719}$
is written
![]() $S^{\unicode[STIX]{x1D719}}$
. As a graded vector space,
$S^{\unicode[STIX]{x1D719}}$
. As a graded vector space,
![]() $S^{\unicode[STIX]{x1D719}}$
is isomorphic to
$S^{\unicode[STIX]{x1D719}}$
is isomorphic to
![]() $S$
. The multiplication
$S$
. The multiplication
![]() $\circ$
on
$\circ$
on
![]() $S^{\unicode[STIX]{x1D719}}$
is defined by
$S^{\unicode[STIX]{x1D719}}$
is defined by
![]() $r\circ s=r\ast \unicode[STIX]{x1D719}^{i}(s)$
for all
$r\circ s=r\ast \unicode[STIX]{x1D719}^{i}(s)$
for all
![]() $r\in S_{i}^{\unicode[STIX]{x1D719}}=S_{i}$
and
$r\in S_{i}^{\unicode[STIX]{x1D719}}=S_{i}$
and
![]() $s\in S_{j}^{\unicode[STIX]{x1D719}}=S_{j}$
. This is associative by [Reference ZhangZha96, Proposition 2.3].
$s\in S_{j}^{\unicode[STIX]{x1D719}}=S_{j}$
. This is associative by [Reference ZhangZha96, Proposition 2.3].
In the terminology of [Reference ZhangZha96] the family of maps
![]() $\{\unicode[STIX]{x1D719}^{i}~|~i\in \mathbb{N}\}$
is a twisting system of
$\{\unicode[STIX]{x1D719}^{i}~|~i\in \mathbb{N}\}$
is a twisting system of
![]() $S$
. We note that the definition in [Reference ZhangZha96] is slightly more general than the one we give here, but we do not need this greater generality.
$S$
. We note that the definition in [Reference ZhangZha96] is slightly more general than the one we give here, but we do not need this greater generality.
Also recall that we may define a left-hand Zhang twist of
![]() $S$
by
$S$
by
![]() $\unicode[STIX]{x1D719}$
, which we write
$\unicode[STIX]{x1D719}$
, which we write
![]() $^{\unicode[STIX]{x1D719}}S$
. The multiplication
$^{\unicode[STIX]{x1D719}}S$
. The multiplication
![]() $\circ ^{\prime }$
on
$\circ ^{\prime }$
on
![]() $^{\unicode[STIX]{x1D719}}S$
is defined by
$^{\unicode[STIX]{x1D719}}S$
is defined by
![]() $r\circ ^{\prime }s=\unicode[STIX]{x1D719}^{j}(r)\ast s$
for all
$r\circ ^{\prime }s=\unicode[STIX]{x1D719}^{j}(r)\ast s$
for all
![]() $r\in ^{\unicode[STIX]{x1D719}}S_{i}=S_{i}$
and
$r\in ^{\unicode[STIX]{x1D719}}S_{i}=S_{i}$
and
![]() $s\in ^{\unicode[STIX]{x1D719}}S_{j}=S_{j}$
. This is associative by [Reference ZhangZha96, Proposition 4.2]. We have the following easy lemma.
$s\in ^{\unicode[STIX]{x1D719}}S_{j}=S_{j}$
. This is associative by [Reference ZhangZha96, Proposition 4.2]. We have the following easy lemma.
Lemma 4.1. Let
![]() $S$
be an
$S$
be an
![]() $\mathbb{N}$
-graded ring with multiplication
$\mathbb{N}$
-graded ring with multiplication
![]() $\ast$
, and let
$\ast$
, and let
![]() $\unicode[STIX]{x1D719}\in \operatorname{Aut}(S)$
be a graded automorphism of
$\unicode[STIX]{x1D719}\in \operatorname{Aut}(S)$
be a graded automorphism of
![]() $S$
. Then
$S$
. Then
![]() $S^{\unicode[STIX]{x1D719}}\cong ^{\unicode[STIX]{x1D719}^{-1}}S$
.
$S^{\unicode[STIX]{x1D719}}\cong ^{\unicode[STIX]{x1D719}^{-1}}S$
.
Proof. Define
![]() $\unicode[STIX]{x1D6F7}:S^{\unicode[STIX]{x1D719}}\rightarrow ^{\unicode[STIX]{x1D719}^{-1}}S$
by
$\unicode[STIX]{x1D6F7}:S^{\unicode[STIX]{x1D719}}\rightarrow ^{\unicode[STIX]{x1D719}^{-1}}S$
by
![]() $\unicode[STIX]{x1D6F7}(t)=\unicode[STIX]{x1D719}^{-k}(t)$
for all
$\unicode[STIX]{x1D6F7}(t)=\unicode[STIX]{x1D719}^{-k}(t)$
for all
![]() $t\in S_{k}^{\unicode[STIX]{x1D719}}$
.
$t\in S_{k}^{\unicode[STIX]{x1D719}}$
.
We denote the multiplication on
![]() $S^{\unicode[STIX]{x1D719}}$
by
$S^{\unicode[STIX]{x1D719}}$
by
![]() $\circ$
and the multiplication on
$\circ$
and the multiplication on
![]() $^{\unicode[STIX]{x1D719}^{-1}}S$
by
$^{\unicode[STIX]{x1D719}^{-1}}S$
by
![]() $\circ ^{\prime }$
. Then for
$\circ ^{\prime }$
. Then for
![]() $r\in S_{i},s\in S_{j}$
, we have
$r\in S_{i},s\in S_{j}$
, we have
since
![]() $\unicode[STIX]{x1D719}$
is an algebra automorphism of
$\unicode[STIX]{x1D719}$
is an algebra automorphism of
![]() $S$
. Thus
$S$
. Thus
as needed. ◻
The first goal of this section is to prove the following theorem
Theorem 4.2. Fix
![]() $n\in \mathbb{Z}_{{\geqslant}0}$
. For any
$n\in \mathbb{Z}_{{\geqslant}0}$
. For any
![]() $a,b\in \Bbbk$
, the rings
$a,b\in \Bbbk$
, the rings
![]() $R(n,a)$
and
$R(n,a)$
and
![]() $R(n,b)$
are right and left Zhang twists of each other.
$R(n,b)$
are right and left Zhang twists of each other.
We prove this by constructing some explicit graded automorphisms of
![]() $R(n,a)$
.
$R(n,a)$
.
Lemma 4.3. For any
![]() $a\in \Bbbk$
, the map
$a\in \Bbbk$
, the map
induces a
![]() $d$
-graded automorphism of
$d$
-graded automorphism of
![]() $R(n,a)$
, which we also denote
$R(n,a)$
, which we also denote
![]() $\unicode[STIX]{x1D719}_{a}$
.
$\unicode[STIX]{x1D719}_{a}$
.
Proof. Note that
Thus
![]() $\unicode[STIX]{x1D719}_{a}$
is simply the automorphism of
$\unicode[STIX]{x1D719}_{a}$
is simply the automorphism of
![]() $R(n,a)$
induced by conjugating by the normal element
$R(n,a)$
induced by conjugating by the normal element
![]() $X_{0}$
.◻
$X_{0}$
.◻
Proposition 4.4. For any
![]() $a\in \Bbbk$
, let
$a\in \Bbbk$
, let
![]() $\unicode[STIX]{x1D719}_{a}$
be the automorphism of
$\unicode[STIX]{x1D719}_{a}$
be the automorphism of
![]() $R(n,a)$
defined in Lemma 4.3. Then
$R(n,a)$
defined in Lemma 4.3. Then
![]() $R(n,0)\cong R(n,a)^{\unicode[STIX]{x1D719}_{a}}$
, under the map induced by sending
$R(n,0)\cong R(n,a)^{\unicode[STIX]{x1D719}_{a}}$
, under the map induced by sending
![]() $X_{i}\mapsto X_{i}$
.
$X_{i}\mapsto X_{i}$
.
Proof. By Lemmas 4.1, and 3.10, it suffices to prove that
![]() $R(n,0)\cong ^{\unicode[STIX]{x1D719}_{-a}}R(n,a)$
. Let
$R(n,0)\cong ^{\unicode[STIX]{x1D719}_{-a}}R(n,a)$
. Let
![]() $\circ$
denote the multiplication on
$\circ$
denote the multiplication on
![]() $^{\unicode[STIX]{x1D719}_{-a}}R(n,a)$
. Then for any
$^{\unicode[STIX]{x1D719}_{-a}}R(n,a)$
. Then for any
![]() $i$
and
$i$
and
![]() $j$
, we have
$j$
, we have
 $$\begin{eqnarray}\displaystyle X_{i}\circ X_{j}=\unicode[STIX]{x1D719}_{-a}(X_{i})\ast X_{j} & = & \displaystyle \mathop{\sum }_{\ell =0}^{i}\binom{-a}{\ell }X_{i-\ell }\ast X_{j}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\ell =0}^{i}\mathop{\sum }_{k=0}^{j-\ell }\binom{-a}{\ell }\binom{a+j}{k}X_{i-\ell -k}X_{j}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{u=0}^{i}\mathop{\sum }_{v=0}^{u}\binom{-a}{v}\binom{a+j}{u-v}X_{i-u}X_{j}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{u=0}^{i}\binom{j}{u}X_{i-u}X_{j},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{i}\circ X_{j}=\unicode[STIX]{x1D719}_{-a}(X_{i})\ast X_{j} & = & \displaystyle \mathop{\sum }_{\ell =0}^{i}\binom{-a}{\ell }X_{i-\ell }\ast X_{j}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\ell =0}^{i}\mathop{\sum }_{k=0}^{j-\ell }\binom{-a}{\ell }\binom{a+j}{k}X_{i-\ell -k}X_{j}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{u=0}^{i}\mathop{\sum }_{v=0}^{u}\binom{-a}{v}\binom{a+j}{u-v}X_{i-u}X_{j}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{u=0}^{i}\binom{j}{u}X_{i-u}X_{j},\nonumber\end{eqnarray}$$
where we have used the Chu-Vandermonde identity at the end. This agrees with the formula for multiplication in
![]() $R(n,0)$
.◻
$R(n,0)$
.◻
As a corollary of Proposition 4.4 we obtain that
![]() $\unicode[STIX]{x1D719}_{b}$
induces an automorphism of
$\unicode[STIX]{x1D719}_{b}$
induces an automorphism of
![]() $R(n,a)$
for any
$R(n,a)$
for any
![]() $a,b$
. For we have
$a,b$
. For we have
Lemma 4.5. Let
![]() $S$
be an
$S$
be an
![]() $\mathbb{N}$
-graded ring and let
$\mathbb{N}$
-graded ring and let
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $\unicode[STIX]{x1D713}$
be graded automorphisms of
$\unicode[STIX]{x1D713}$
be graded automorphisms of
![]() $S$
such that
$S$
such that
![]() $\unicode[STIX]{x1D719}\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}\unicode[STIX]{x1D719}$
. Then
$\unicode[STIX]{x1D719}\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}\unicode[STIX]{x1D719}$
. Then
![]() $\unicode[STIX]{x1D713}$
is also an automorphism of
$\unicode[STIX]{x1D713}$
is also an automorphism of
![]() $S^{\unicode[STIX]{x1D719}}$
and
$S^{\unicode[STIX]{x1D719}}$
and
![]() $^{\unicode[STIX]{x1D719}}S$
.
$^{\unicode[STIX]{x1D719}}S$
.
Proof. We prove the lemma for
![]() $S^{\unicode[STIX]{x1D719}}$
; note the statement makes sense because as a graded vector space
$S^{\unicode[STIX]{x1D719}}$
; note the statement makes sense because as a graded vector space
![]() $S=S^{\unicode[STIX]{x1D719}}$
. Let
$S=S^{\unicode[STIX]{x1D719}}$
. Let
![]() $\ast$
denote the multiplication on
$\ast$
denote the multiplication on
![]() $S$
and let
$S$
and let
![]() $\circ$
denote the multiplication on
$\circ$
denote the multiplication on
![]() $S^{\unicode[STIX]{x1D719}}$
. We check that for any
$S^{\unicode[STIX]{x1D719}}$
. We check that for any
![]() $r\in S_{i}$
and
$r\in S_{i}$
and
![]() $s\in S_{j}$
, we have
$s\in S_{j}$
, we have
as needed. ◻
Corollary 4.6. Fix
![]() $n\in \mathbb{Z}_{{>}0}$
. For any
$n\in \mathbb{Z}_{{>}0}$
. For any
![]() $a,b\in \Bbbk$
, the action of
$a,b\in \Bbbk$
, the action of
![]() $\unicode[STIX]{x1D719}_{b}$
on
$\unicode[STIX]{x1D719}_{b}$
on
![]() $R(n,a)$
induces an automorphism of
$R(n,a)$
induces an automorphism of
![]() $R(n,a)$
.
$R(n,a)$
.
Proof. That
![]() $\unicode[STIX]{x1D719}_{b}$
induces an automorphism of
$\unicode[STIX]{x1D719}_{b}$
induces an automorphism of
![]() $R(n,0)$
for any
$R(n,0)$
for any
![]() $b$
follows from Lemma 4.5, with
$b$
follows from Lemma 4.5, with
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}_{b}$
. We then apply Lemma 4.5 again, using the facts that
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}_{b}$
. We then apply Lemma 4.5 again, using the facts that
![]() $\unicode[STIX]{x1D719}_{a}\unicode[STIX]{x1D719}_{b}=\unicode[STIX]{x1D719}_{a+b}=\unicode[STIX]{x1D719}_{b}\unicode[STIX]{x1D719}_{a}$
and that
$\unicode[STIX]{x1D719}_{a}\unicode[STIX]{x1D719}_{b}=\unicode[STIX]{x1D719}_{a+b}=\unicode[STIX]{x1D719}_{b}\unicode[STIX]{x1D719}_{a}$
and that
![]() $R(n,a)\cong ^{\unicode[STIX]{x1D719}_{a}}R(n,0)$
proved in Proposition 4.4.◻
$R(n,a)\cong ^{\unicode[STIX]{x1D719}_{a}}R(n,0)$
proved in Proposition 4.4.◻
Corollary 4.7. For any
![]() $a,b\in \Bbbk$
, we have
$a,b\in \Bbbk$
, we have
![]() $^{\unicode[STIX]{x1D719}_{b}}R(n,a)\cong R(n,a+b)$
, under the map
$^{\unicode[STIX]{x1D719}_{b}}R(n,a)\cong R(n,a+b)$
, under the map
![]() $X_{i}\mapsto X_{i}$
.
$X_{i}\mapsto X_{i}$
.
Proof. The proof is very similar to the proof of Proposition 4.4 and is left to the reader. ◻
Proof of Theorem 4.2.
The result follows immediately from Corollary 4.7, using Lemma 4.1 to move from left to right twists. ◻
We now show that up to composition with nonzero scalar multiplication, the only nontrivial graded automorphisms of
![]() $R(n,a)$
are the maps
$R(n,a)$
are the maps
![]() $\unicode[STIX]{x1D719}_{b}$
. We need the following lemma.
$\unicode[STIX]{x1D719}_{b}$
. We need the following lemma.
Lemma 4.8. Let
![]() $n\geqslant 2$
. Suppose that
$n\geqslant 2$
. Suppose that
![]() $\unicode[STIX]{x1D713}\in \operatorname{Aut}R(n,a)$
is such that
$\unicode[STIX]{x1D713}\in \operatorname{Aut}R(n,a)$
is such that
![]() $\unicode[STIX]{x1D713}(X_{0})=X_{0}$
and
$\unicode[STIX]{x1D713}(X_{0})=X_{0}$
and
![]() $\unicode[STIX]{x1D713}(X_{j})=X_{j}+\unicode[STIX]{x1D6FC}_{j}X_{0}$
with
$\unicode[STIX]{x1D713}(X_{j})=X_{j}+\unicode[STIX]{x1D6FC}_{j}X_{0}$
with
![]() $\unicode[STIX]{x1D6FC}_{j}\in \Bbbk$
for
$\unicode[STIX]{x1D6FC}_{j}\in \Bbbk$
for
![]() $1\leqslant j\leqslant n$
. Then
$1\leqslant j\leqslant n$
. Then
![]() $\unicode[STIX]{x1D713}$
is the identity.
$\unicode[STIX]{x1D713}$
is the identity.
Proof. By applying
![]() $\unicode[STIX]{x1D713}$
to the second equation of (3.18) we obtain
$\unicode[STIX]{x1D713}$
to the second equation of (3.18) we obtain
Thus we have
![]() $\unicode[STIX]{x1D6FC}_{1}=0$
when
$\unicode[STIX]{x1D6FC}_{1}=0$
when
![]() $a\neq 0$
. If
$a\neq 0$
. If
![]() $a=0$
we apply
$a=0$
we apply
![]() $\unicode[STIX]{x1D713}$
to the third equation of (3.18) to get
$\unicode[STIX]{x1D713}$
to the third equation of (3.18) to get
Again we must have
![]() $\unicode[STIX]{x1D6FC}_{1}=0$
. Now suppose that
$\unicode[STIX]{x1D6FC}_{1}=0$
. Now suppose that
![]() $\unicode[STIX]{x1D6FC}_{j}=0$
for
$\unicode[STIX]{x1D6FC}_{j}=0$
for
![]() $1\leqslant j<k$
. We apply the automorphism
$1\leqslant j<k$
. We apply the automorphism
![]() $\unicode[STIX]{x1D713}$
to the relation (3.13) with
$\unicode[STIX]{x1D713}$
to the relation (3.13) with
![]() $i=1$
and
$i=1$
and
![]() $j=k$
. After rearranging we get
$j=k$
. After rearranging we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle X_{1}\ast (X_{k}+\unicode[STIX]{x1D6FC}_{k}X_{0})-(a+k)X_{0}\ast (X_{k}+\unicode[STIX]{x1D6FC}_{k}X_{0})\nonumber\\ \displaystyle & & \displaystyle \quad =(X_{k}+\unicode[STIX]{x1D6FC}_{k}X_{0})\ast X_{1}+\mathop{\sum }_{j=1}^{k}\binom{-a-1}{j}X_{k-j}\ast X_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle X_{1}\ast (X_{k}+\unicode[STIX]{x1D6FC}_{k}X_{0})-(a+k)X_{0}\ast (X_{k}+\unicode[STIX]{x1D6FC}_{k}X_{0})\nonumber\\ \displaystyle & & \displaystyle \quad =(X_{k}+\unicode[STIX]{x1D6FC}_{k}X_{0})\ast X_{1}+\mathop{\sum }_{j=1}^{k}\binom{-a-1}{j}X_{k-j}\ast X_{1}.\end{eqnarray}$$
Thanks to Equation (3.1) we compare the coefficients of the
![]() $X_{0}^{2}$
term in both sides of the equality (4.9) and we obtain
$X_{0}^{2}$
term in both sides of the equality (4.9) and we obtain
![]() $\unicode[STIX]{x1D6FC}_{k}(a-(a+k))=0$
. So
$\unicode[STIX]{x1D6FC}_{k}(a-(a+k))=0$
. So
![]() $-k\unicode[STIX]{x1D6FC}_{k}=0$
and
$-k\unicode[STIX]{x1D6FC}_{k}=0$
and
![]() $\unicode[STIX]{x1D6FC}_{k}=0$
since
$\unicode[STIX]{x1D6FC}_{k}=0$
since
![]() $k\neq 0$
.◻
$k\neq 0$
.◻
We can now determine the graded automorphism group
![]() $\operatorname{Aut}_{\operatorname{gr}}R(n,a)$
of
$\operatorname{Aut}_{\operatorname{gr}}R(n,a)$
of
![]() $R(n,a)$
. For
$R(n,a)$
. For
![]() $\unicode[STIX]{x1D706}\in \Bbbk ^{\times }$
, let
$\unicode[STIX]{x1D706}\in \Bbbk ^{\times }$
, let
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}$
be the automorphism that scales all
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}$
be the automorphism that scales all
![]() $X_{i}$
by
$X_{i}$
by
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
Theorem 4.10. Assume either that
![]() $n\geqslant 2$
or that
$n\geqslant 2$
or that
![]() $n=1$
and
$n=1$
and
![]() $a\neq 0$
. The
$a\neq 0$
. The
![]() $d$
-graded automorphisms of
$d$
-graded automorphisms of
![]() $R(n,a)$
are of the form
$R(n,a)$
are of the form
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D719}_{c}$
, for some
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D719}_{c}$
, for some
![]() $\unicode[STIX]{x1D706}\in \Bbbk ^{\times }$
and
$\unicode[STIX]{x1D706}\in \Bbbk ^{\times }$
and
![]() $c\in \Bbbk$
. In particular we have
$c\in \Bbbk$
. In particular we have
![]() $\operatorname{Aut}_{\operatorname{gr}}R(n,a)\cong \Bbbk ^{\times }\times \Bbbk$
.
$\operatorname{Aut}_{\operatorname{gr}}R(n,a)\cong \Bbbk ^{\times }\times \Bbbk$
.
Proof. It follows from Corollary 4.6 that the maps
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D719}_{c}$
are indeed automorphisms of
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D719}_{c}$
are indeed automorphisms of
![]() $R(n,a)$
. Reciprocally, we proceed by induction on
$R(n,a)$
. Reciprocally, we proceed by induction on
![]() $n$
. We first assume that
$n$
. We first assume that
![]() $a\neq -(n-1)$
. For
$a\neq -(n-1)$
. For
![]() $n=1$
(and
$n=1$
(and
![]() $a\neq 0$
), the result follows from [Reference ShirikovShi05, Theorem 3.1]. We assume that the result is true for
$a\neq 0$
), the result follows from [Reference ShirikovShi05, Theorem 3.1]. We assume that the result is true for
![]() $R(n-1,b)$
with
$R(n-1,b)$
with
![]() $b\neq -(n-2)$
. Let
$b\neq -(n-2)$
. Let
![]() $\unicode[STIX]{x1D713}$
be a
$\unicode[STIX]{x1D713}$
be a
![]() $d$
-graded automorphism of
$d$
-graded automorphism of
![]() $R(n,a)$
. Thanks to Proposition 3.21 the only normal elements of
$R(n,a)$
. Thanks to Proposition 3.21 the only normal elements of
![]() $R(n,a)$
with
$R(n,a)$
with
![]() $d$
-degree
$d$
-degree
![]() $1$
are the nonzero scalar multiples of
$1$
are the nonzero scalar multiples of
![]() $X_{0}$
. Thus, up to composition with some
$X_{0}$
. Thus, up to composition with some
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}$
, we have that
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}$
, we have that
![]() $\unicode[STIX]{x1D713}(X_{0})=X_{0}$
. In particular
$\unicode[STIX]{x1D713}(X_{0})=X_{0}$
. In particular
![]() $\unicode[STIX]{x1D713}$
induces a
$\unicode[STIX]{x1D713}$
induces a
![]() $d$
-graded automorphism of
$d$
-graded automorphism of
![]() $R(n,a)/\langle X_{0}\rangle \cong R(n-1,a+1)$
. By the induction hypothesis we have
$R(n,a)/\langle X_{0}\rangle \cong R(n-1,a+1)$
. By the induction hypothesis we have
![]() $\unicode[STIX]{x1D713}(X_{j})=\sum _{i=0}^{j-1}\unicode[STIX]{x1D706}\binom{c}{i}X_{j-i}+\unicode[STIX]{x1D6FC}_{j}X_{0}$
for any
$\unicode[STIX]{x1D713}(X_{j})=\sum _{i=0}^{j-1}\unicode[STIX]{x1D706}\binom{c}{i}X_{j-i}+\unicode[STIX]{x1D6FC}_{j}X_{0}$
for any
![]() $j\geqslant 1$
, where
$j\geqslant 1$
, where
![]() $\unicode[STIX]{x1D706}\in \Bbbk ^{\times }$
and
$\unicode[STIX]{x1D706}\in \Bbbk ^{\times }$
and
![]() $c,\unicode[STIX]{x1D6FC}_{j}\in \Bbbk$
. We obtain that
$c,\unicode[STIX]{x1D6FC}_{j}\in \Bbbk$
. We obtain that
![]() $\unicode[STIX]{x1D706}=1$
by applying
$\unicode[STIX]{x1D706}=1$
by applying
![]() $\unicode[STIX]{x1D719}$
to the first equation of (3.18) when
$\unicode[STIX]{x1D719}$
to the first equation of (3.18) when
![]() $a\neq 0$
, or to the third equation of (3.18) when
$a\neq 0$
, or to the third equation of (3.18) when
![]() $a=0$
. In particular we have
$a=0$
. In particular we have
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}_{c}$
modulo
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}_{c}$
modulo
![]() $X_{0}$
, and by applying Lemma 4.8 to
$X_{0}$
, and by applying Lemma 4.8 to
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D719}_{-c}$
we conclude that
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D719}_{-c}$
we conclude that
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}_{c}$
.
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}_{c}$
.
We finally deal with the case
![]() $a=-(n-1)$
. We prove by induction on
$a=-(n-1)$
. We prove by induction on
![]() $n\geqslant 2$
that the
$n\geqslant 2$
that the
![]() $d$
-graded automorphisms of
$d$
-graded automorphisms of
![]() $R(n,-(n-1))$
are of the form
$R(n,-(n-1))$
are of the form
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D719}_{c}$
. We only prove the base case of the induction since the induction step of the previous induction will also apply to that case. Let
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D719}_{c}$
. We only prove the base case of the induction since the induction step of the previous induction will also apply to that case. Let
![]() $\unicode[STIX]{x1D713}$
be a
$\unicode[STIX]{x1D713}$
be a
![]() $d$
-graded automorphism of
$d$
-graded automorphism of
![]() $R(2,-1)$
. Then
$R(2,-1)$
. Then
![]() $\unicode[STIX]{x1D713}(X_{0})=\unicode[STIX]{x1D706}X_{0}$
for some nonzero
$\unicode[STIX]{x1D713}(X_{0})=\unicode[STIX]{x1D706}X_{0}$
for some nonzero
![]() $\unicode[STIX]{x1D706}$
, and by rescaling we may assume that
$\unicode[STIX]{x1D706}$
, and by rescaling we may assume that
![]() $\unicode[STIX]{x1D706}=1$
. Further,
$\unicode[STIX]{x1D706}=1$
. Further,
![]() $\unicode[STIX]{x1D713}$
induces a
$\unicode[STIX]{x1D713}$
induces a
![]() $d$
-graded automorphism of the commutative polynomial ring
$d$
-graded automorphism of the commutative polynomial ring
![]() $R(2,-1)/\langle X_{0}\rangle \cong R(1,0)\cong \Bbbk [X_{1},X_{2}]$
. Therefore, there exist
$R(2,-1)/\langle X_{0}\rangle \cong R(1,0)\cong \Bbbk [X_{1},X_{2}]$
. Therefore, there exist
![]() $c,d,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$
such that
$c,d,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$
such that
![]() $\unicode[STIX]{x1D713}(X_{1})=\unicode[STIX]{x1D6FC}X_{2}+\unicode[STIX]{x1D6FD}X_{1}+cX_{0}$
and
$\unicode[STIX]{x1D713}(X_{1})=\unicode[STIX]{x1D6FC}X_{2}+\unicode[STIX]{x1D6FD}X_{1}+cX_{0}$
and
![]() $\unicode[STIX]{x1D713}(X_{2})=\unicode[STIX]{x1D6FE}X_{2}+\unicode[STIX]{x1D6FF}X_{1}+dX_{0}$
, where
$\unicode[STIX]{x1D713}(X_{2})=\unicode[STIX]{x1D6FE}X_{2}+\unicode[STIX]{x1D6FF}X_{1}+dX_{0}$
, where
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\neq 0$
.
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\neq 0$
.
Applying
![]() $\unicode[STIX]{x1D713}$
to the relations (3.18) we obtain that
$\unicode[STIX]{x1D713}$
to the relations (3.18) we obtain that
![]() $\unicode[STIX]{x1D6FC}=0$
,
$\unicode[STIX]{x1D6FC}=0$
,
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FE}=1$
,
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FE}=1$
,
![]() $\unicode[STIX]{x1D6FF}=c$
and
$\unicode[STIX]{x1D6FF}=c$
and
![]() $d=\binom{c}{2}$
. This shows that
$d=\binom{c}{2}$
. This shows that
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}_{c}$
and concludes the proof.◻
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}_{c}$
and concludes the proof.◻
One can prove a similar version of Proposition 4.10 for the Poisson algebra
![]() $A(n,a)$
. For any
$A(n,a)$
. For any
![]() $c\in \Bbbk$
the maps
$c\in \Bbbk$
the maps
![]() $\unicode[STIX]{x1D711}_{c}:=\exp (c\unicode[STIX]{x1D6E5})$
are well-defined automorphisms of the commutative polynomial ring
$\unicode[STIX]{x1D711}_{c}:=\exp (c\unicode[STIX]{x1D6E5})$
are well-defined automorphisms of the commutative polynomial ring
![]() $A(n,a)$
since
$A(n,a)$
since
![]() $\unicode[STIX]{x1D6E5}$
is a locally nilpotent derivation. Moreover, we observe that
$\unicode[STIX]{x1D6E5}$
is a locally nilpotent derivation. Moreover, we observe that
for all
![]() $0\leqslant i,j\leqslant n$
. This shows that
$0\leqslant i,j\leqslant n$
. This shows that
![]() $\unicode[STIX]{x1D6E5}$
is a Poisson derivation of
$\unicode[STIX]{x1D6E5}$
is a Poisson derivation of
![]() $A(n,a)$
, and thus the maps
$A(n,a)$
, and thus the maps
![]() $\unicode[STIX]{x1D711}_{c}$
are Poisson automorphisms of
$\unicode[STIX]{x1D711}_{c}$
are Poisson automorphisms of
![]() $A(n,a)$
.
$A(n,a)$
.
We state the following result without proof.
Proposition 4.11. Assume either that
![]() $n\geqslant 2$
or that
$n\geqslant 2$
or that
![]() $a\neq 0$
. The
$a\neq 0$
. The
![]() $d$
-graded Poisson automorphisms of
$d$
-graded Poisson automorphisms of
![]() $A(n,a)$
are of the form
$A(n,a)$
are of the form
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D711}_{c}$
, for some
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D711}_{c}$
, for some
![]() $\unicode[STIX]{x1D706}\in \Bbbk ^{\times }$
and
$\unicode[STIX]{x1D706}\in \Bbbk ^{\times }$
and
![]() $c\in \Bbbk$
. In particular the graded Poisson automorphism group
$c\in \Bbbk$
. In particular the graded Poisson automorphism group
![]() $\operatorname{PAut}_{\text{gr}}A(n,a)$
of
$\operatorname{PAut}_{\text{gr}}A(n,a)$
of
![]() $A(n,a)$
is isomorphic to
$A(n,a)$
is isomorphic to
![]() $\Bbbk ^{\times }\times \Bbbk$
.
$\Bbbk ^{\times }\times \Bbbk$
.
Corollary 4.12. Assume either that
![]() $n\geqslant 2$
or that
$n\geqslant 2$
or that
![]() $a\neq 0$
. Then
$a\neq 0$
. Then
When
![]() $n=1$
and
$n=1$
and
![]() $a=0$
we have
$a=0$
we have
Remark 4.13. We note that for certain values of
![]() $a$
, there exist nongraded (Poisson) automorphisms. For instance it is well known that for any polynomial
$a$
, there exist nongraded (Poisson) automorphisms. For instance it is well known that for any polynomial
![]() $P\in \Bbbk [X_{0}]$
the map sending
$P\in \Bbbk [X_{0}]$
the map sending
![]() $X_{0}\mapsto X_{0}$
and
$X_{0}\mapsto X_{0}$
and
![]() $X_{1}\mapsto X_{1}+P$
defines an automorphism of the Jordan plane
$X_{1}\mapsto X_{1}+P$
defines an automorphism of the Jordan plane
![]() $R(1,a)$
and the Poisson–Jordan plane
$R(1,a)$
and the Poisson–Jordan plane
![]() $A(1,a)$
. When
$A(1,a)$
. When
![]() $n=2$
and
$n=2$
and
![]() $a=1/q$
for some
$a=1/q$
for some
![]() $q\in \mathbb{Z}_{{>}0}$
, the map
$q\in \mathbb{Z}_{{>}0}$
, the map
![]() $f$
defined by
$f$
defined by
is a nongraded Poisson automorphism of
![]() $A(2,1/q)$
.
$A(2,1/q)$
.
To conclude this section we calculate the Nakayama automorphism of
![]() $R(n,a)$
and prove, in particular, that
$R(n,a)$
and prove, in particular, that
![]() $R(n,-\frac{1}{2}(n+2)(n-1)/(n+1))$
is
$R(n,-\frac{1}{2}(n+2)(n-1)/(n+1))$
is
![]() $(n+1)$
-Calabi–Yau for every
$(n+1)$
-Calabi–Yau for every
![]() $n>0$
. We first recall some definitions. Let
$n>0$
. We first recall some definitions. Let
![]() $R$
be a
$R$
be a
![]() $\Bbbk$
-algebra, and let
$\Bbbk$
-algebra, and let
![]() $R^{e}=R\otimes _{\Bbbk }R^{op}$
be the enveloping algebra of
$R^{e}=R\otimes _{\Bbbk }R^{op}$
be the enveloping algebra of
![]() $R$
. An
$R$
. An
![]() $(R,R)$
-bimodule
$(R,R)$
-bimodule
![]() $M$
can be considered as a left
$M$
can be considered as a left
![]() $R^{e}$
-module by defining
$R^{e}$
-module by defining
![]() $r\otimes s\cdot m=rms$
.
$r\otimes s\cdot m=rms$
.
Definition 4.14. We say that
![]() $R$
is skew Calabi–Yau (or skew CY) if
$R$
is skew Calabi–Yau (or skew CY) if
(i)
 $R$
is homologically smooth:
$R$
is homologically smooth:
 $R$
has a finite projective resolution as a left
$R$
has a finite projective resolution as a left
 $R^{e}$
-module such that each term is finitely generated;
$R^{e}$
-module such that each term is finitely generated;(ii) There are an algebra automorphism
 $\unicode[STIX]{x1D707}$
of
$\unicode[STIX]{x1D707}$
of
 $R$
and an integer
$R$
and an integer
 $d$
such that (Here
$d$
such that (Here $$\begin{eqnarray}\operatorname{Ext}_{R^{e}}^{i}(R,R^{e})\cong \left\{\begin{array}{@{}ll@{}}0\quad & \text{if }i\neq 0\\ \text{}^{1}R^{\unicode[STIX]{x1D707}}\quad & \text{if }i=d.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}_{R^{e}}^{i}(R,R^{e})\cong \left\{\begin{array}{@{}ll@{}}0\quad & \text{if }i\neq 0\\ \text{}^{1}R^{\unicode[STIX]{x1D707}}\quad & \text{if }i=d.\end{array}\right.\end{eqnarray}$$
 $^{1}R^{\unicode[STIX]{x1D707}}$
is the
$^{1}R^{\unicode[STIX]{x1D707}}$
is the
 $R$
-bimodule which is isomorphic to
$R$
-bimodule which is isomorphic to
 $R$
as a
$R$
as a
 $\Bbbk$
-vector space and such that
$\Bbbk$
-vector space and such that
 $r\cdot s\cdot t=rs\unicode[STIX]{x1D707}(t)$
.)
$r\cdot s\cdot t=rs\unicode[STIX]{x1D707}(t)$
.)
If
![]() $R$
is skew CY, the automorphism
$R$
is skew CY, the automorphism
![]() $\unicode[STIX]{x1D707}$
is called the Nakayama automorphism of
$\unicode[STIX]{x1D707}$
is called the Nakayama automorphism of
![]() $R$
. If
$R$
. If
![]() $\unicode[STIX]{x1D707}$
is inner, then
$\unicode[STIX]{x1D707}$
is inner, then
![]() $R$
is Calabi–Yau or CY.
$R$
is Calabi–Yau or CY.
By [Reference Reyes, Rogalski and ZhangRRZ14, Lemma 1.2], any AS-regular connected graded algebra is skew CY. In particular, the algebras
![]() $R(n,a)$
are skew CY.
$R(n,a)$
are skew CY.
We need the following lemma before calculating the Nakayama automorphism of
![]() $R(n,a)$
.
$R(n,a)$
.
Lemma 4.15. Let
![]() $\unicode[STIX]{x1D707}$
be the Nakayama automorphism of
$\unicode[STIX]{x1D707}$
be the Nakayama automorphism of
![]() $R=R(n,a)$
for any
$R=R(n,a)$
for any
![]() $n\geqslant 1$
. Then for all
$n\geqslant 1$
. Then for all
![]() $0\leqslant j\leqslant n$
, we have
$0\leqslant j\leqslant n$
, we have
![]() $\unicode[STIX]{x1D707}(X_{j})-X_{j}\in \operatorname{span}(X_{0},\ldots ,X_{j-1})$
. In particular
$\unicode[STIX]{x1D707}(X_{j})-X_{j}\in \operatorname{span}(X_{0},\ldots ,X_{j-1})$
. In particular
![]() $\unicode[STIX]{x1D707}(X_{0})=X_{0}$
.
$\unicode[STIX]{x1D707}(X_{0})=X_{0}$
.
Proof. The Nakayama automorphism of the commutative polynomial ring
![]() $A=\Bbbk [X_{0},\ldots ,X_{n}]$
is well known to be trivial. Since
$A=\Bbbk [X_{0},\ldots ,X_{n}]$
is well known to be trivial. Since
![]() $A$
is the associated graded of
$A$
is the associated graded of
![]() $R$
with respect to the
$R$
with respect to the
![]() $\unicode[STIX]{x1D716}$
-filtration and clearly
$\unicode[STIX]{x1D716}$
-filtration and clearly
![]() $A^{e}\cong \Bbbk [X_{0},\ldots ,X_{2n+1}]$
is the associated graded of
$A^{e}\cong \Bbbk [X_{0},\ldots ,X_{2n+1}]$
is the associated graded of
![]() $R^{e}$
, by [Reference BjörkBjö89, Proposition 3.1], we have that the associated graded of
$R^{e}$
, by [Reference BjörkBjö89, Proposition 3.1], we have that the associated graded of
![]() $\operatorname{Ext}_{R^{e}}^{n}(R,R^{e})=^{1}R^{\unicode[STIX]{x1D707}}$
is a subquotient of
$\operatorname{Ext}_{R^{e}}^{n}(R,R^{e})=^{1}R^{\unicode[STIX]{x1D707}}$
is a subquotient of
![]() $\operatorname{Ext}_{A^{e}}^{n}(A,A^{e})=^{1}A^{1}$
. This shows that the
$\operatorname{Ext}_{A^{e}}^{n}(A,A^{e})=^{1}A^{1}$
. This shows that the
![]() $\unicode[STIX]{x1D716}$
-leading term of
$\unicode[STIX]{x1D716}$
-leading term of
![]() $\unicode[STIX]{x1D707}(X_{j})$
must be
$\unicode[STIX]{x1D707}(X_{j})$
must be
![]() $X_{j}$
.◻
$X_{j}$
.◻
Theorem 4.16. For any
![]() $n\geqslant 1$
, the Nakayama automorphism of
$n\geqslant 1$
, the Nakayama automorphism of
![]() $R(n,a)$
is
$R(n,a)$
is
![]() $\unicode[STIX]{x1D719}_{c}$
, where
$\unicode[STIX]{x1D719}_{c}$
, where
Proof. We begin by calculating the Nakayama automorphism of
![]() $R(n,0)$
. For
$R(n,0)$
. For
![]() $n=1$
we have
$n=1$
we have
![]() $R(1,0)\cong \Bbbk [X_{0},X_{1}]$
, so the Nakayama automorphism is the identity
$R(1,0)\cong \Bbbk [X_{0},X_{1}]$
, so the Nakayama automorphism is the identity
![]() $\unicode[STIX]{x1D719}_{0}$
; we have
$\unicode[STIX]{x1D719}_{0}$
; we have
![]() $0=\binom{2}{2}-1$
. Suppose now that
$0=\binom{2}{2}-1$
. Suppose now that
![]() $n>1$
and we wish to calculate the Nakayama automorphism
$n>1$
and we wish to calculate the Nakayama automorphism
![]() $\unicode[STIX]{x1D707}$
of
$\unicode[STIX]{x1D707}$
of
![]() $R(n,0)$
. Let
$R(n,0)$
. Let
![]() $b=n+\binom{n}{2}-1=\binom{n+1}{2}-1$
. Since by Lemma 4.15 we have
$b=n+\binom{n}{2}-1=\binom{n+1}{2}-1$
. Since by Lemma 4.15 we have
![]() $\unicode[STIX]{x1D707}(X_{0})=X_{0}$
, thus
$\unicode[STIX]{x1D707}(X_{0})=X_{0}$
, thus
![]() $\unicode[STIX]{x1D707}$
induces an automorphism of
$\unicode[STIX]{x1D707}$
induces an automorphism of
![]() $R(n,0)/\langle X_{0}\rangle \cong R(n-1,1)$
. By [Reference Reyes, Rogalski and ZhangRRZ14, Lemma 1.5], using the fact that
$R(n,0)/\langle X_{0}\rangle \cong R(n-1,1)$
. By [Reference Reyes, Rogalski and ZhangRRZ14, Lemma 1.5], using the fact that
![]() $X_{0}$
is central, this induced automorphism is equal to the Nakayama automorphism of
$X_{0}$
is central, this induced automorphism is equal to the Nakayama automorphism of
![]() $R(n-1,1)$
, which by induction on
$R(n-1,1)$
, which by induction on
![]() $n$
is
$n$
is
![]() $\unicode[STIX]{x1D719}_{b}$
. Thus modulo
$\unicode[STIX]{x1D719}_{b}$
. Thus modulo
![]() $X_{0}$
, we have that
$X_{0}$
, we have that
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D719}_{b}$
. By applying Lemma 4.8 to
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D719}_{b}$
. By applying Lemma 4.8 to
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D719}_{-b}$
we see that
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D719}_{-b}$
we see that
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D719}_{b}$
.
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D719}_{b}$
.
Let
![]() $\unicode[STIX]{x1D707}$
be the Nakayama automorphism of
$\unicode[STIX]{x1D707}$
be the Nakayama automorphism of
![]() $R(n,0)$
and
$R(n,0)$
and
![]() $\unicode[STIX]{x1D708}$
be the Nakayama automorphism of
$\unicode[STIX]{x1D708}$
be the Nakayama automorphism of
![]() $R(n,a)=^{\unicode[STIX]{x1D719}_{a}}R(n,0)$
. By [Reference Reyes, Rogalski and ZhangRRZ14, Theorem 0.3], we have
$R(n,a)=^{\unicode[STIX]{x1D719}_{a}}R(n,0)$
. By [Reference Reyes, Rogalski and ZhangRRZ14, Theorem 0.3], we have
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}\unicode[STIX]{x1D719}_{a}^{n+1}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}$
for some
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}\unicode[STIX]{x1D719}_{a}^{n+1}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}$
for some
![]() $\unicode[STIX]{x1D706}\in \Bbbk ^{\times }$
. By Lemma 4.15, we must have
$\unicode[STIX]{x1D706}\in \Bbbk ^{\times }$
. By Lemma 4.15, we must have
![]() $\unicode[STIX]{x1D706}=1$
. Thus
$\unicode[STIX]{x1D706}=1$
. Thus
as claimed. ◻
Corollary 4.17. For any
![]() $n\geqslant 1$
, the algebra
$n\geqslant 1$
, the algebra
![]() $R(n,a)$
is Calabi–Yau if and only if
$R(n,a)$
is Calabi–Yau if and only if
5 Isomorphisms
We have seen in Example 3.16 that we have
![]() $R(1,0)\cong R(1,a)$
$R(1,0)\cong R(1,a)$
![]() $\;\Longleftrightarrow \;$
$\;\Longleftrightarrow \;$
![]() $a=0$
and that
$a=0$
and that
![]() $R(1,a)\cong R(1,b)$
for any nonzero
$R(1,a)\cong R(1,b)$
for any nonzero
![]() $a,b\in \Bbbk$
. A similar statement holds for the Poisson algebras
$a,b\in \Bbbk$
. A similar statement holds for the Poisson algebras
![]() $A(1,a)$
. In this section we analyze the isomorphism question for
$A(1,a)$
. In this section we analyze the isomorphism question for
![]() $R(n,a)$
and
$R(n,a)$
and
![]() $A(n,a)$
where
$A(n,a)$
where
![]() $n\geqslant 2$
. Moreover, we show that each
$n\geqslant 2$
. Moreover, we show that each
![]() $R(n,a)$
is isomorphic to its opposite ring.
$R(n,a)$
is isomorphic to its opposite ring.
The main theorem of this section is the next result.
Theorem 5.1. Let
![]() $n\geqslant 2$
and let
$n\geqslant 2$
and let
![]() $a,a^{\prime }\in \Bbbk$
. The following are equivalent:
$a,a^{\prime }\in \Bbbk$
. The following are equivalent:
(1)
 $a=a^{\prime }$
;
$a=a^{\prime }$
;(2)
 $R(n,a)\cong R(n,a^{\prime })$
;
$R(n,a)\cong R(n,a^{\prime })$
;(3)
 $A(n,a)$
is Poisson isomorphic to
$A(n,a)$
is Poisson isomorphic to
 $A(n,a^{\prime })$
.
$A(n,a^{\prime })$
.
We remark that Theorem 5.1 is not particularly surprising given Corollary 4.17, since for each
![]() $n$
there is a unique
$n$
there is a unique
![]() $a$
with
$a$
with
![]() $R(n,a)$
Calabi–Yau.
$R(n,a)$
Calabi–Yau.
Proof of Theorem 5.1.
![]() $(1)\Rightarrow (2),(3)$
is trivial.
$(1)\Rightarrow (2),(3)$
is trivial.
![]() $(3)\Rightarrow (1)$
. Let
$(3)\Rightarrow (1)$
. Let
![]() $A=A(n,a)$
and let
$A=A(n,a)$
and let
![]() $A^{\prime }=A(n,a^{\prime })$
. To avoid any confusion, we denote the generators of
$A^{\prime }=A(n,a^{\prime })$
. To avoid any confusion, we denote the generators of
![]() $A$
by
$A$
by
![]() $X_{0},\ldots ,X_{n}$
as usual and denote the corresponding generators of
$X_{0},\ldots ,X_{n}$
as usual and denote the corresponding generators of
![]() $A^{\prime }$
by
$A^{\prime }$
by
![]() $X_{0}^{\prime },\ldots ,X_{n}^{\prime }$
. We let
$X_{0}^{\prime },\ldots ,X_{n}^{\prime }$
. We let
![]() $\unicode[STIX]{x1D6E5}$
also denote the downward derivation on
$\unicode[STIX]{x1D6E5}$
also denote the downward derivation on
![]() $A^{\prime }$
, so
$A^{\prime }$
, so
![]() $\unicode[STIX]{x1D6E5}(X_{i}^{\prime })=X_{i-1}^{\prime }$
.
$\unicode[STIX]{x1D6E5}(X_{i}^{\prime })=X_{i-1}^{\prime }$
.
Suppose that there is a Poisson isomorphism
![]() $\unicode[STIX]{x1D6FC}:A\rightarrow A^{\prime }$
. For
$\unicode[STIX]{x1D6FC}:A\rightarrow A^{\prime }$
. For
![]() $0\leqslant i\leqslant n$
set
$0\leqslant i\leqslant n$
set
![]() $\unicode[STIX]{x1D6FC}(X_{i})=T_{i}=L_{i}+P_{i}$
, where
$\unicode[STIX]{x1D6FC}(X_{i})=T_{i}=L_{i}+P_{i}$
, where
![]() $L_{i}\in A_{1}^{\prime }$
and
$L_{i}\in A_{1}^{\prime }$
and
![]() $P_{i}\in \Bbbk \oplus \bigoplus _{k\geqslant 2}A_{k}^{\prime }$
. Note that since
$P_{i}\in \Bbbk \oplus \bigoplus _{k\geqslant 2}A_{k}^{\prime }$
. Note that since
![]() $\unicode[STIX]{x1D6FC}$
can be seen as an algebra automorphism of the polynomial ring
$\unicode[STIX]{x1D6FC}$
can be seen as an algebra automorphism of the polynomial ring
![]() $A$
, the linear parts
$A$
, the linear parts
![]() $L_{i}$
must be nonzero for all
$L_{i}$
must be nonzero for all
![]() $0\leqslant i\leqslant n$
(using the fact that the Jacobian of
$0\leqslant i\leqslant n$
(using the fact that the Jacobian of
![]() $\unicode[STIX]{x1D6FC}$
must be nonzero at the origin).
$\unicode[STIX]{x1D6FC}$
must be nonzero at the origin).
If
![]() $a=0$
then since
$a=0$
then since
![]() $X_{0}$
is Poisson central
$X_{0}$
is Poisson central
![]() $T_{0}$
must be as well. As the Poisson bracket respects the
$T_{0}$
must be as well. As the Poisson bracket respects the
![]() $d$
-grading on
$d$
-grading on
![]() $A^{\prime }$
, the degree 1 part
$A^{\prime }$
, the degree 1 part
![]() $L_{0}$
must be Poisson central and by Proposition 3.21 we have
$L_{0}$
must be Poisson central and by Proposition 3.21 we have
![]() $L_{0}\in \ker \unicode[STIX]{x1D6E5}$
. Thus
$L_{0}\in \ker \unicode[STIX]{x1D6E5}$
. Thus
![]() $L_{0}=\unicode[STIX]{x1D706}_{0}X_{0}^{\prime }$
is Poisson central and so
$L_{0}=\unicode[STIX]{x1D706}_{0}X_{0}^{\prime }$
is Poisson central and so
![]() $a^{\prime }=0$
. This shows that
$a^{\prime }=0$
. This shows that
![]() $a=0$
$a=0$
![]() $\;\Longleftrightarrow \;$
$\;\Longleftrightarrow \;$
![]() $a^{\prime }=0$
.
$a^{\prime }=0$
.
Suppose now that
![]() $aa^{\prime }\neq 0$
. Now
$aa^{\prime }\neq 0$
. Now
![]() $T_{0}$
is Poisson normal and by Proposition 3.21 we have
$T_{0}$
is Poisson normal and by Proposition 3.21 we have
![]() $T_{0}\in \ker \unicode[STIX]{x1D6E5}$
and
$T_{0}\in \ker \unicode[STIX]{x1D6E5}$
and
![]() $T_{0}$
is a
$T_{0}$
is a
![]() $\unicode[STIX]{x1D6E4}_{a^{\prime }}$
-eigenvector. Thus
$\unicode[STIX]{x1D6E4}_{a^{\prime }}$
-eigenvector. Thus
![]() $L_{0}\in \ker \unicode[STIX]{x1D6E5}$
and so
$L_{0}\in \ker \unicode[STIX]{x1D6E5}$
and so
![]() $L_{0}=\unicode[STIX]{x1D706}_{0}X_{0}^{\prime }$
for some
$L_{0}=\unicode[STIX]{x1D706}_{0}X_{0}^{\prime }$
for some
![]() $0\neq \unicode[STIX]{x1D706}_{0}\in \Bbbk$
. Since
$0\neq \unicode[STIX]{x1D706}_{0}\in \Bbbk$
. Since
![]() $\unicode[STIX]{x1D6E4}_{a^{\prime }}(L_{0})=a^{\prime }L_{0}$
we have
$\unicode[STIX]{x1D6E4}_{a^{\prime }}(L_{0})=a^{\prime }L_{0}$
we have
![]() $\unicode[STIX]{x1D6E4}_{a^{\prime }}(T_{0})=a^{\prime }T_{0}$
.
$\unicode[STIX]{x1D6E4}_{a^{\prime }}(T_{0})=a^{\prime }T_{0}$
.
Let
![]() $c=a/a^{\prime }\neq 0$
. Applying
$c=a/a^{\prime }\neq 0$
. Applying
![]() $\unicode[STIX]{x1D6FC}$
to the equation
$\unicode[STIX]{x1D6FC}$
to the equation
![]() $a\unicode[STIX]{x1D6E5}(g)X_{0}=\{g,X_{0}\}_{a}$
we obtain
$a\unicode[STIX]{x1D6E5}(g)X_{0}=\{g,X_{0}\}_{a}$
we obtain
and so
as maps from
![]() $A\rightarrow A^{\prime }$
. Since
$A\rightarrow A^{\prime }$
. Since
![]() $\unicode[STIX]{x1D6E5}$
respects the
$\unicode[STIX]{x1D6E5}$
respects the
![]() $d$
-degree we have
$d$
-degree we have
![]() $\unicode[STIX]{x1D6E5}(L_{i})=cL_{i-1}$
for
$\unicode[STIX]{x1D6E5}(L_{i})=cL_{i-1}$
for
![]() $1\leqslant i\leqslant n$
. Thus there are
$1\leqslant i\leqslant n$
. Thus there are
![]() $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in \Bbbk$
so that
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in \Bbbk$
so that
 $$\begin{eqnarray}\displaystyle L_{0} & = & \displaystyle \unicode[STIX]{x1D706}_{0}X_{0}^{\prime },\nonumber\\ \displaystyle L_{1} & = & \displaystyle c\unicode[STIX]{x1D706}_{0}X_{1}^{\prime }+\unicode[STIX]{x1D706}_{1}X_{0}^{\prime },\nonumber\\ \displaystyle L_{2} & = & \displaystyle c^{2}\unicode[STIX]{x1D706}_{0}X_{2}^{\prime }+c\unicode[STIX]{x1D706}_{1}X_{1}^{\prime }+\unicode[STIX]{x1D706}_{2}X_{0}^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L_{0} & = & \displaystyle \unicode[STIX]{x1D706}_{0}X_{0}^{\prime },\nonumber\\ \displaystyle L_{1} & = & \displaystyle c\unicode[STIX]{x1D706}_{0}X_{1}^{\prime }+\unicode[STIX]{x1D706}_{1}X_{0}^{\prime },\nonumber\\ \displaystyle L_{2} & = & \displaystyle c^{2}\unicode[STIX]{x1D706}_{0}X_{2}^{\prime }+c\unicode[STIX]{x1D706}_{1}X_{1}^{\prime }+\unicode[STIX]{x1D706}_{2}X_{0}^{\prime }.\nonumber\end{eqnarray}$$
From (5.2) we also conclude that
![]() $T_{0},T_{1}\in \operatorname{Im}\unicode[STIX]{x1D6E5}$
and so have no constant term. Considering the equality
$T_{0},T_{1}\in \operatorname{Im}\unicode[STIX]{x1D6E5}$
and so have no constant term. Considering the equality
then gives that
![]() $T_{2}$
has no constant term. Therefore, the
$T_{2}$
has no constant term. Therefore, the
![]() $X_{0}^{\prime }X_{2}^{\prime }$
term of the left-hand side of (5.3) is
$X_{0}^{\prime }X_{2}^{\prime }$
term of the left-hand side of (5.3) is
![]() $(a+2)c^{2}\unicode[STIX]{x1D706}_{1}^{2}X_{0}^{\prime }X_{2}^{\prime }$
. On the other hand, the
$(a+2)c^{2}\unicode[STIX]{x1D706}_{1}^{2}X_{0}^{\prime }X_{2}^{\prime }$
. On the other hand, the
![]() $X_{0}^{\prime }X_{2}^{\prime }$
term of the right-hand side is
$X_{0}^{\prime }X_{2}^{\prime }$
term of the right-hand side is
![]() $\unicode[STIX]{x1D6E5}(c\unicode[STIX]{x1D706}_{0}X_{1}^{\prime })\unicode[STIX]{x1D6E4}_{a^{\prime }}(c^{2}\unicode[STIX]{x1D706}_{0}X_{2}^{\prime })=c^{3}\unicode[STIX]{x1D706}_{0}^{2}(a^{\prime }+2)X_{0}^{\prime }X_{2}^{\prime }$
. Thus
$\unicode[STIX]{x1D6E5}(c\unicode[STIX]{x1D706}_{0}X_{1}^{\prime })\unicode[STIX]{x1D6E4}_{a^{\prime }}(c^{2}\unicode[STIX]{x1D706}_{0}X_{2}^{\prime })=c^{3}\unicode[STIX]{x1D706}_{0}^{2}(a^{\prime }+2)X_{0}^{\prime }X_{2}^{\prime }$
. Thus
![]() $a+2/a=a^{\prime }+2/a^{\prime }$
and
$a+2/a=a^{\prime }+2/a^{\prime }$
and
![]() $a^{\prime }=a$
.
$a^{\prime }=a$
.
![]() $(2)\Rightarrow (1)$
. Let
$(2)\Rightarrow (1)$
. Let
![]() $R=R(n,a)$
and let
$R=R(n,a)$
and let
![]() $R^{\prime }=R(n,a^{\prime })$
. As above, we denote the generators of
$R^{\prime }=R(n,a^{\prime })$
. As above, we denote the generators of
![]() $R^{\prime }$
by
$R^{\prime }$
by
![]() $X_{0}^{\prime },\ldots ,X_{n}^{\prime }$
. If
$X_{0}^{\prime },\ldots ,X_{n}^{\prime }$
. If
![]() $R\cong R^{\prime }$
then by [Reference Bell and ZhangBZ17, Theorem 0.1] there exists a graded isomorphism
$R\cong R^{\prime }$
then by [Reference Bell and ZhangBZ17, Theorem 0.1] there exists a graded isomorphism
![]() $\unicode[STIX]{x1D6FC}:R\rightarrow R^{\prime }$
. Since
$\unicode[STIX]{x1D6FC}:R\rightarrow R^{\prime }$
. Since
![]() $X_{0}$
is normal in
$X_{0}$
is normal in
![]() $R_{1}$
its image
$R_{1}$
its image
![]() $\unicode[STIX]{x1D6FC}(X_{0})$
is normal in
$\unicode[STIX]{x1D6FC}(X_{0})$
is normal in
![]() $R_{1}^{\prime }$
and
$R_{1}^{\prime }$
and
![]() $\unicode[STIX]{x1D6FC}(X_{0})\in \operatorname{span}(X_{0}^{\prime })$
thanks to Proposition 3.21. We prove the result by induction on
$\unicode[STIX]{x1D6FC}(X_{0})\in \operatorname{span}(X_{0}^{\prime })$
thanks to Proposition 3.21. We prove the result by induction on
![]() $n$
.
$n$
.
We first consider the case
![]() $n=2$
. Since
$n=2$
. Since
![]() $X_{0}$
is central if and only if
$X_{0}$
is central if and only if
![]() $a=0$
we deduce that
$a=0$
we deduce that
![]() $a=0\;\Longleftrightarrow \;a^{\prime }=0$
. Therefore, we may assume that
$a=0\;\Longleftrightarrow \;a^{\prime }=0$
. Therefore, we may assume that
![]() $a,a^{\prime }\neq 0$
in the following. Since
$a,a^{\prime }\neq 0$
in the following. Since
![]() $\unicode[STIX]{x1D6FC}(X_{1})\in R_{1}^{\prime }$
there exist scalars
$\unicode[STIX]{x1D6FC}(X_{1})\in R_{1}^{\prime }$
there exist scalars
![]() $\unicode[STIX]{x1D707}_{0},\unicode[STIX]{x1D707}_{1}$
and
$\unicode[STIX]{x1D707}_{0},\unicode[STIX]{x1D707}_{1}$
and
![]() $\unicode[STIX]{x1D707}_{2}$
not all zero such that
$\unicode[STIX]{x1D707}_{2}$
not all zero such that
![]() $\unicode[STIX]{x1D6FC}(X_{1})=\unicode[STIX]{x1D707}_{0}X_{0}^{\prime }+\unicode[STIX]{x1D707}_{1}X_{1}^{\prime }+\unicode[STIX]{x1D707}_{2}X_{2}^{\prime }$
. We fix
$\unicode[STIX]{x1D6FC}(X_{1})=\unicode[STIX]{x1D707}_{0}X_{0}^{\prime }+\unicode[STIX]{x1D707}_{1}X_{1}^{\prime }+\unicode[STIX]{x1D707}_{2}X_{2}^{\prime }$
. We fix
![]() $\unicode[STIX]{x1D706}_{0}\in \Bbbk ^{\times }$
such that
$\unicode[STIX]{x1D706}_{0}\in \Bbbk ^{\times }$
such that
![]() $\unicode[STIX]{x1D6FC}(X_{0})=\unicode[STIX]{x1D706}_{0}X_{0}^{\prime }$
. By applying
$\unicode[STIX]{x1D6FC}(X_{0})=\unicode[STIX]{x1D706}_{0}X_{0}^{\prime }$
. By applying
![]() $\unicode[STIX]{x1D6FC}$
to the first equality in (3.18) we obtain
$\unicode[STIX]{x1D6FC}$
to the first equality in (3.18) we obtain
After simplification using the relations (3.18) we compare the coefficients of the
![]() $X_{0}^{\prime }\ast X_{1}^{\prime }$
term. We get
$X_{0}^{\prime }\ast X_{1}^{\prime }$
term. We get
![]() $-a^{\prime }\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D707}_{2}=0$
which implies that
$-a^{\prime }\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D707}_{2}=0$
which implies that
![]() $\unicode[STIX]{x1D707}_{2}=0$
since
$\unicode[STIX]{x1D707}_{2}=0$
since
![]() $a^{\prime }\neq 0$
. In particular we have
$a^{\prime }\neq 0$
. In particular we have
![]() $\unicode[STIX]{x1D6FC}(X_{1})\in \operatorname{span}(X_{0}^{\prime },X_{1}^{\prime })$
and
$\unicode[STIX]{x1D6FC}(X_{1})\in \operatorname{span}(X_{0}^{\prime },X_{1}^{\prime })$
and
![]() $\unicode[STIX]{x1D6FC}$
respects the
$\unicode[STIX]{x1D6FC}$
respects the
![]() $\unicode[STIX]{x1D716}$
-filtrations on
$\unicode[STIX]{x1D716}$
-filtrations on
![]() $R$
and
$R$
and
![]() $R^{\prime }$
. By Lemma 3.5
$R^{\prime }$
. By Lemma 3.5
![]() $\unicode[STIX]{x1D6FC}$
induces a Poisson isomorphism between
$\unicode[STIX]{x1D6FC}$
induces a Poisson isomorphism between
![]() $A(2,a)$
and
$A(2,a)$
and
![]() $A(2,a^{\prime })$
, so
$A(2,a^{\prime })$
, so
![]() $a=a^{\prime }$
.
$a=a^{\prime }$
.
Suppose now
![]() $n\geqslant 3$
and the result true for
$n\geqslant 3$
and the result true for
![]() $n-1$
. Since
$n-1$
. Since
![]() $\unicode[STIX]{x1D6FC}(X_{0})\in \operatorname{span}(X_{0}^{\prime })$
there is an isomorphism
$\unicode[STIX]{x1D6FC}(X_{0})\in \operatorname{span}(X_{0}^{\prime })$
there is an isomorphism
![]() $R(n-1,a+1)\cong R/\langle X_{0}\rangle \rightarrow R^{\prime }/\langle X_{0}^{\prime }\rangle \cong R(n-1,a^{\prime }+1)$
and we have
$R(n-1,a+1)\cong R/\langle X_{0}\rangle \rightarrow R^{\prime }/\langle X_{0}^{\prime }\rangle \cong R(n-1,a^{\prime }+1)$
and we have
![]() $a+1=a^{\prime }+1$
.◻
$a+1=a^{\prime }+1$
.◻
To end the section we prove that
![]() $R(n,a)$
and
$R(n,a)$
and
![]() $R(n,a)^{\text{op}}$
are isomorphic. This will be used in the next section.
$R(n,a)^{\text{op}}$
are isomorphic. This will be used in the next section.
Theorem 5.4. For any
![]() $u\in \Bbbk$
, the map
$u\in \Bbbk$
, the map
![]() $\unicode[STIX]{x1D714}_{u}$
from
$\unicode[STIX]{x1D714}_{u}$
from
![]() $R(n,a)$
to
$R(n,a)$
to
![]() $R(n,a)$
defined by
$R(n,a)$
defined by
is an anti-isomorphism. In particular
![]() $R(n,a)$
and
$R(n,a)$
and
![]() $R(n,a)^{\text{op}}$
are isomorphic for any
$R(n,a)^{\text{op}}$
are isomorphic for any
![]() $a\in \Bbbk$
and any
$a\in \Bbbk$
and any
![]() $n>0$
.
$n>0$
.
We need the following lemmas.
Lemma 5.5. For any
![]() $v\in \mathbb{N}$
and
$v\in \mathbb{N}$
and
![]() $a,m\in \Bbbk$
we have
$a,m\in \Bbbk$
we have
Proof. The proof is a combination of the Chu-Vandermonde identity (3.9) and the identity
for any
![]() $\ell \in \mathbb{N}$
and
$\ell \in \mathbb{N}$
and
![]() $u\in \Bbbk$
.◻
$u\in \Bbbk$
.◻
Lemma 5.7. For
![]() $a,u\in \Bbbk$
we have
$a,u\in \Bbbk$
we have
Proof. We have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{u}\unicode[STIX]{x1D719}_{a}(X_{i}) & = & \displaystyle \mathop{\sum }_{k=0}^{i}\binom{a}{k}\mathop{\sum }_{\ell =0}^{i-k}(-1)^{i-k}\binom{i-k-u}{\ell }X_{i-k-\ell }\nonumber\\ \displaystyle & = & \displaystyle (-1)^{i}\mathop{\sum }_{k=0}^{i}\mathop{\sum }_{\ell =0}^{i-k}(-1)^{-k}\binom{a}{k}\binom{i-k-u}{\ell }X_{i-k-\ell }\nonumber\\ \displaystyle & = & \displaystyle (-1)^{i}\mathop{\sum }_{v=0}^{i}\mathop{\sum }_{k=0}^{v}(-1)^{-k}\binom{a}{k}\binom{i-k-u}{v-k}X_{i-v}\nonumber\\ \displaystyle & = & \displaystyle (-1)^{i}\mathop{\sum }_{v=0}^{i}\binom{i-(u+a)}{v}X_{i-v}=w_{a+u}(X_{i}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{u}\unicode[STIX]{x1D719}_{a}(X_{i}) & = & \displaystyle \mathop{\sum }_{k=0}^{i}\binom{a}{k}\mathop{\sum }_{\ell =0}^{i-k}(-1)^{i-k}\binom{i-k-u}{\ell }X_{i-k-\ell }\nonumber\\ \displaystyle & = & \displaystyle (-1)^{i}\mathop{\sum }_{k=0}^{i}\mathop{\sum }_{\ell =0}^{i-k}(-1)^{-k}\binom{a}{k}\binom{i-k-u}{\ell }X_{i-k-\ell }\nonumber\\ \displaystyle & = & \displaystyle (-1)^{i}\mathop{\sum }_{v=0}^{i}\mathop{\sum }_{k=0}^{v}(-1)^{-k}\binom{a}{k}\binom{i-k-u}{v-k}X_{i-v}\nonumber\\ \displaystyle & = & \displaystyle (-1)^{i}\mathop{\sum }_{v=0}^{i}\binom{i-(u+a)}{v}X_{i-v}=w_{a+u}(X_{i}),\nonumber\end{eqnarray}$$
where we have set
![]() $v=k+\ell$
and then use Lemma 5.5 with
$v=k+\ell$
and then use Lemma 5.5 with
![]() $m=i-u$
.◻
$m=i-u$
.◻
Proof of Theorem 5.4.
Note that the relations (3.14) in
![]() $R(n,a)$
can be rewritten as
$R(n,a)$
can be rewritten as
for any
![]() $0\leqslant i,j\leqslant n$
. To see that
$0\leqslant i,j\leqslant n$
. To see that
![]() $\unicode[STIX]{x1D714}_{u}$
is a well-defined anti-automorphism of
$\unicode[STIX]{x1D714}_{u}$
is a well-defined anti-automorphism of
![]() $R(n,a)$
it is enough to apply
$R(n,a)$
it is enough to apply
![]() $\unicode[STIX]{x1D714}_{u}$
to both side of (5.9) and check that we obtain the same result. Using (5.8) we have
$\unicode[STIX]{x1D714}_{u}$
to both side of (5.9) and check that we obtain the same result. Using (5.8) we have
and similarly
For any
![]() $c\in \Bbbk$
the map
$c\in \Bbbk$
the map
![]() $\unicode[STIX]{x1D719}_{c}$
is an automorphism of
$\unicode[STIX]{x1D719}_{c}$
is an automorphism of
![]() $R(n,a)$
, and by applying
$R(n,a)$
, and by applying
![]() $\unicode[STIX]{x1D719}_{c}$
to (5.9) we obtain that
$\unicode[STIX]{x1D719}_{c}$
to (5.9) we obtain that
Letting
![]() $c=a+i+j-u=i-u+z_{j}=j-u+z_{i}$
we deduce that
$c=a+i+j-u=i-u+z_{j}=j-u+z_{i}$
we deduce that
This proves that
![]() $\unicode[STIX]{x1D714}_{u}(\unicode[STIX]{x1D719}_{-z_{i}}(X_{j})\ast X_{i})=\unicode[STIX]{x1D714}_{u}(\unicode[STIX]{x1D719}_{-z_{j}}(X_{i})\ast X_{j})$
and finishes the proof.◻
$\unicode[STIX]{x1D714}_{u}(\unicode[STIX]{x1D719}_{-z_{i}}(X_{j})\ast X_{i})=\unicode[STIX]{x1D714}_{u}(\unicode[STIX]{x1D719}_{-z_{j}}(X_{i})\ast X_{j})$
and finishes the proof.◻
The opposite algebra
![]() $A(n,a)^{\text{op}}$
of the Poisson algebra
$A(n,a)^{\text{op}}$
of the Poisson algebra
![]() $A(n,a)$
is the same associative
$A(n,a)$
is the same associative
![]() $\Bbbk$
-algebra endowed with the opposite Poisson bracket
$\Bbbk$
-algebra endowed with the opposite Poisson bracket
![]() $\{-,-\}^{\text{op}}:=-\{-,-\}$
. The analogue of Theorem 5.4 for
$\{-,-\}^{\text{op}}:=-\{-,-\}$
. The analogue of Theorem 5.4 for
![]() $A(n,a)$
follows easily from Lemma 3.5. It is straightforward to check that the map
$A(n,a)$
follows easily from Lemma 3.5. It is straightforward to check that the map
![]() $\unicode[STIX]{x1D6FD}$
from
$\unicode[STIX]{x1D6FD}$
from
![]() $A(n,a)^{\text{op}}$
to
$A(n,a)^{\text{op}}$
to
![]() $A(n,a)$
sending
$A(n,a)$
sending
![]() $X_{i}$
to
$X_{i}$
to
![]() $(-1)^{i}X_{i}$
for all
$(-1)^{i}X_{i}$
for all
![]() $i$
is a Poisson algebra isomorphism.
$i$
is a Poisson algebra isomorphism.
6 Point modules
Let
![]() $R$
be an
$R$
be an
![]() $\mathbb{N}$
-graded ring. A (left or right) point module over
$\mathbb{N}$
-graded ring. A (left or right) point module over
![]() $R$
is a cyclic graded module
$R$
is a cyclic graded module
![]() $M$
with
$M$
with
![]() $\operatorname{hilb}(M)=1/(1-t)$
. In this section we study the point modules of the
$\operatorname{hilb}(M)=1/(1-t)$
. In this section we study the point modules of the
![]() $R(n,a)$
and prove:
$R(n,a)$
and prove:
Theorem 6.1. Let
![]() $R=R(n,a)$
, where
$R=R(n,a)$
, where
![]() $n\geqslant 1$
. If
$n\geqslant 1$
. If
![]() $M=R/J$
is a right or left point module, then
$M=R/J$
is a right or left point module, then
![]() $J$
is generated by
$J$
is generated by
![]() $J_{1}$
as a right (respectively, left) ideal of
$J_{1}$
as a right (respectively, left) ideal of
![]() $R$
. There is a projective scheme
$R$
. There is a projective scheme
![]() $X$
that parameterizes both left and right point modules, and
$X$
that parameterizes both left and right point modules, and
![]() $X^{\text{red}}$
is isomorphic to
$X^{\text{red}}$
is isomorphic to
![]() $n$
copies of
$n$
copies of
![]() $\mathbb{P}^{1}$
, where the
$\mathbb{P}^{1}$
, where the
![]() $k$
th copy is embedded in
$k$
th copy is embedded in
![]() $V(X_{0},\ldots ,X_{n-k-1})\subseteq \mathbb{P}(R_{1}^{\ast })$
as a rational normal curve of degree
$V(X_{0},\ldots ,X_{n-k-1})\subseteq \mathbb{P}(R_{1}^{\ast })$
as a rational normal curve of degree
![]() $k$
.
$k$
.
Recall that there are normal elements
![]() $Y_{2},\ldots ,Y_{n}$
in
$Y_{2},\ldots ,Y_{n}$
in
![]() $R^{\circ }=R[X_{0}^{-1}]$
. Let
$R^{\circ }=R[X_{0}^{-1}]$
. Let
![]() $T$
be the subalgebra of
$T$
be the subalgebra of
![]() $R^{\circ }$
generated by
$R^{\circ }$
generated by
![]() $X_{0},X_{1},Y_{2},\ldots ,Y_{n}$
. We compute the point modules for
$X_{0},X_{1},Y_{2},\ldots ,Y_{n}$
. We compute the point modules for
![]() $R$
by relating points of
$R$
by relating points of
![]() $R$
to those of
$R$
to those of
![]() $T$
.
$T$
.
Let
![]() $C=\Bbbk [X_{0},Y_{2},\ldots ,Y_{n}]$
. We know from Lemma 3.26 that
$C=\Bbbk [X_{0},Y_{2},\ldots ,Y_{n}]$
. We know from Lemma 3.26 that
![]() $R^{\circ }=C[X_{0}^{-1}][X_{1};\unicode[STIX]{x1D6FF}]$
where
$R^{\circ }=C[X_{0}^{-1}][X_{1};\unicode[STIX]{x1D6FF}]$
where
![]() $\unicode[STIX]{x1D6FF}$
is the derivation
$\unicode[STIX]{x1D6FF}$
is the derivation
![]() $X_{0}\unicode[STIX]{x1D6E4}_{a}$
of
$X_{0}\unicode[STIX]{x1D6E4}_{a}$
of
![]() $C[X_{0}^{-1}]$
. The proof of that result also gives that
$C[X_{0}^{-1}]$
. The proof of that result also gives that
![]() $T=C[X_{1};\unicode[STIX]{x1D6FF}]$
. We then have:
$T=C[X_{1};\unicode[STIX]{x1D6FF}]$
. We then have:
Proposition 6.2.
(1)
 $T$
has
$T$
has
 $\binom{n+1}{2}$
quadratic relations. They are:
$\binom{n+1}{2}$
quadratic relations. They are:  $$\begin{eqnarray}\begin{array}{@{}ccc@{}}A:\quad & X_{1}X_{0}-X_{0}X_{1}-aX_{0}^{2} & \\ A(k): & X_{1}Y_{k}-Y_{k}X_{1}-(a+k)X_{0}Y_{k} & \text{for }2\leqslant k\leqslant n\\ B(k): & X_{0}Y_{k}-Y_{k}X_{0} & \text{for }2\leqslant k\leqslant n\\ C(j,k): & Y_{k}Y_{j}-Y_{j}Y_{k} & \text{for }2\leqslant j<k\leqslant n.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}A:\quad & X_{1}X_{0}-X_{0}X_{1}-aX_{0}^{2} & \\ A(k): & X_{1}Y_{k}-Y_{k}X_{1}-(a+k)X_{0}Y_{k} & \text{for }2\leqslant k\leqslant n\\ B(k): & X_{0}Y_{k}-Y_{k}X_{0} & \text{for }2\leqslant k\leqslant n\\ C(j,k): & Y_{k}Y_{j}-Y_{j}Y_{k} & \text{for }2\leqslant j<k\leqslant n.\end{array}\end{eqnarray}$$
(2)
 $T$
is Artin–Schelter regular.
$T$
is Artin–Schelter regular.
Proof.
![]() $(1)$
is a straightforward computation. For
$(1)$
is a straightforward computation. For
![]() $(2)$
, note that the weight grading
$(2)$
, note that the weight grading
![]() $\unicode[STIX]{x1D716}$
can be used to define a filtration on
$\unicode[STIX]{x1D716}$
can be used to define a filtration on
![]() $T$
whose associated graded ring is the commutative polynomial ring
$T$
whose associated graded ring is the commutative polynomial ring
![]() $C[X_{1}]$
. Thus
$C[X_{1}]$
. Thus
![]() $T$
has finite global dimension. Clearly
$T$
has finite global dimension. Clearly
![]() $T$
has finite Gelfand–Kirillov dimension. Note that
$T$
has finite Gelfand–Kirillov dimension. Note that
![]() $Y_{2},\ldots ,Y_{n}$
are normal in
$Y_{2},\ldots ,Y_{n}$
are normal in
![]() $T$
, and
$T$
, and
![]() $T/(Y_{2},\ldots ,Y_{n})$
is isomorphic to the Jordan plane and is AS-regular. Thus
$T/(Y_{2},\ldots ,Y_{n})$
is isomorphic to the Jordan plane and is AS-regular. Thus
![]() $T$
is AS–Gorenstein by [Reference LevasseurLev92, Corollary 5.10, Theorem 6.3].◻
$T$
is AS–Gorenstein by [Reference LevasseurLev92, Corollary 5.10, Theorem 6.3].◻
By Corollary 3.6
![]() $R$
is strongly Noetherian. Thus by [Reference Artin and ZhangAZ01, Theorem E4.3] there is a projective scheme
$R$
is strongly Noetherian. Thus by [Reference Artin and ZhangAZ01, Theorem E4.3] there is a projective scheme
![]() $X$
that parameterizes right
$X$
that parameterizes right
![]() $R$
-point modules up to isomorphism. For
$R$
-point modules up to isomorphism. For
![]() $x\in X$
, let
$x\in X$
, let
![]() $M(x)$
be the corresponding point module. By [Reference Keeler, Rogalski and StaffordKRS05, Proposition 10.2], there is
$M(x)$
be the corresponding point module. By [Reference Keeler, Rogalski and StaffordKRS05, Proposition 10.2], there is
![]() $\unicode[STIX]{x1D70E}\in \operatorname{Aut}(X)$
so that
$\unicode[STIX]{x1D70E}\in \operatorname{Aut}(X)$
so that
![]() $M(x)[1]_{{\geqslant}0}\cong M(\unicode[STIX]{x1D70E}(x))$
for all
$M(x)[1]_{{\geqslant}0}\cong M(\unicode[STIX]{x1D70E}(x))$
for all
![]() $x\in X$
.
$x\in X$
.
We also have:
Lemma 6.3. If
![]() $M$
is an
$M$
is an
![]() $R$
-point module or a
$R$
-point module or a
![]() $T$
-point module, then either
$T$
-point module, then either
![]() $MX_{0}=0$
or
$MX_{0}=0$
or
![]() $M$
is
$M$
is
![]() $X_{0}$
-torsionfree.
$X_{0}$
-torsionfree.
Proof. This is a consequence of the facts that
![]() $R$
and
$R$
and
![]() $T$
are AS-regular with Hilbert series
$T$
are AS-regular with Hilbert series
![]() $1/(1-t)^{n+1}$
and
$1/(1-t)^{n+1}$
and
![]() $X_{0}$
is a normal element. See [Reference Le Bruyn and SmithLBS93, page 728] for a summary of the argument.◻
$X_{0}$
is a normal element. See [Reference Le Bruyn and SmithLBS93, page 728] for a summary of the argument.◻
We now relate
![]() $X_{0}$
-torsionfree point modules over
$X_{0}$
-torsionfree point modules over
![]() $R$
to point modules over
$R$
to point modules over
![]() $T$
.
$T$
.
Proposition 6.4. Let
![]() $M$
be an
$M$
be an
![]() $X_{0}$
-torsionfree point module over
$X_{0}$
-torsionfree point module over
![]() $R$
. Then there is a unique
$R$
. Then there is a unique
![]() $T$
-action on
$T$
-action on
![]() $M$
that extends the action of
$M$
that extends the action of
![]() $T\cap R$
and makes
$T\cap R$
and makes
![]() $M$
a
$M$
a
![]() $T$
-point module.
$T$
-point module.
Similarly, if
![]() $L$
is an
$L$
is an
![]() $X_{0}$
-torsionfree point module over
$X_{0}$
-torsionfree point module over
![]() $T$
then there is a unique
$T$
then there is a unique
![]() $R$
-action on
$R$
-action on
![]() $L$
that extends the action of
$L$
that extends the action of
![]() $T\cap R$
and makes
$T\cap R$
and makes
![]() $L$
also a point module over
$L$
also a point module over
![]() $R$
.
$R$
.
Proof. Let
![]() $x\in X$
and recall the isomorphism
$x\in X$
and recall the isomorphism
![]() $M(x)[1]_{{\geqslant}0}\cong M(\unicode[STIX]{x1D70E}(x))$
. Equivalently, there are inclusions
$M(x)[1]_{{\geqslant}0}\cong M(\unicode[STIX]{x1D70E}(x))$
. Equivalently, there are inclusions
![]() $M(x)\subseteq M(\unicode[STIX]{x1D70E}^{-1}(x))[1]$
for all
$M(x)\subseteq M(\unicode[STIX]{x1D70E}^{-1}(x))[1]$
for all
![]() $x\in X$
. Note also that because
$x\in X$
. Note also that because
![]() $\unicode[STIX]{x1D70E}\in \operatorname{Aut}(X)$
, the point
$\unicode[STIX]{x1D70E}\in \operatorname{Aut}(X)$
, the point
![]() $\unicode[STIX]{x1D70E}^{-1}(x)$
is the unique
$\unicode[STIX]{x1D70E}^{-1}(x)$
is the unique
![]() $y\in X$
so that
$y\in X$
so that
![]() $M(x)\subseteq M(y)[1]$
. Let
$M(x)\subseteq M(y)[1]$
. Let
The module
![]() $N(x)$
is
$N(x)$
is
![]() $\mathbb{Z}$
-graded with
$\mathbb{Z}$
-graded with
![]() $\dim N(x)_{k}=1$
for all
$\dim N(x)_{k}=1$
for all
![]() $k\in \mathbb{Z}$
. (In fact,
$k\in \mathbb{Z}$
. (In fact,
![]() $N(x)$
is the injective hull of
$N(x)$
is the injective hull of
![]() $M(x)$
in the category of graded
$M(x)$
in the category of graded
![]() $R$
-modules.)
$R$
-modules.)
Suppose now that
![]() $M(x)$
is
$M(x)$
is
![]() $X_{0}$
-torsionfree. By Lemma 6.3 so is each
$X_{0}$
-torsionfree. By Lemma 6.3 so is each
![]() $M(\unicode[STIX]{x1D70E}^{-n}(x))$
, as
$M(\unicode[STIX]{x1D70E}^{-n}(x))$
, as
![]() $M(x)\subseteq M(\unicode[STIX]{x1D70E}^{-n}(x))[n]$
. Thus
$M(x)\subseteq M(\unicode[STIX]{x1D70E}^{-n}(x))[n]$
. Thus
![]() $N(x)$
is
$N(x)$
is
![]() $X_{0}$
-torsionfree. We may thus choose a basis
$X_{0}$
-torsionfree. We may thus choose a basis
![]() $\{n_{k}\mid k\in \mathbb{Z}\}$
of
$\{n_{k}\mid k\in \mathbb{Z}\}$
of
![]() $N(x)$
with
$N(x)$
with
![]() $n_{k}\in N(x)_{k}$
and
$n_{k}\in N(x)_{k}$
and
![]() $n_{k}X_{0}=n_{k+1}$
. If we define
$n_{k}X_{0}=n_{k+1}$
. If we define
![]() $n_{k}X_{0}^{-1}=n_{k-1}$
for all
$n_{k}X_{0}^{-1}=n_{k-1}$
for all
![]() $k\in \mathbb{Z}$
, we obtain an action of
$k\in \mathbb{Z}$
, we obtain an action of
![]() $R[X_{0}^{-1}]$
on
$R[X_{0}^{-1}]$
on
![]() $N(x)$
, and thus an action of
$N(x)$
, and thus an action of
![]() $T$
on
$T$
on
![]() $N(x)_{{\geqslant}0}=M(x)$
. The action is clearly unique.
$N(x)_{{\geqslant}0}=M(x)$
. The action is clearly unique.
The proof that an
![]() $X_{0}$
-torsionfree point module over
$X_{0}$
-torsionfree point module over
![]() $T$
has an induced
$T$
has an induced
![]() $R$
-action is similar.
$R$
-action is similar.
If
![]() $K$
is an
$K$
is an
![]() $X_{0}$
-torsionfree point module over
$X_{0}$
-torsionfree point module over
![]() $T$
(or over
$T$
(or over
![]() $R$
) then
$R$
) then
![]() $K$
is cyclic as a module over
$K$
is cyclic as a module over
![]() $\Bbbk [X_{0}]$
. Thus
$\Bbbk [X_{0}]$
. Thus
![]() $K$
is also cyclic under the induced
$K$
is also cyclic under the induced
![]() $R$
-action (or
$R$
-action (or
![]() $T$
-action).◻
$T$
-action).◻
We now compute the point modules of
![]() $T$
, at least up to radical. Let
$T$
, at least up to radical. Let
![]() $V:=T/\langle Y_{2},\ldots ,Y_{n}\rangle$
. We have
$V:=T/\langle Y_{2},\ldots ,Y_{n}\rangle$
. We have
![]() $V\cong k\langle X_{0},X_{1}\rangle /\langle X_{1}X_{0}-X_{0}X_{1}-aX_{0}^{2}\rangle$
. If
$V\cong k\langle X_{0},X_{1}\rangle /\langle X_{1}X_{0}-X_{0}X_{1}-aX_{0}^{2}\rangle$
. If
![]() $a\neq 0$
, this ring is the Jordan plane; in particular, the
$a\neq 0$
, this ring is the Jordan plane; in particular, the
![]() $V$
are isomorphic for any
$V$
are isomorphic for any
![]() $a\neq 0$
. If
$a\neq 0$
. If
![]() $a=0$
, then
$a=0$
, then
![]() $V$
is a commutative polynomial ring.
$V$
is a commutative polynomial ring.
Proposition 6.5. The reduced point scheme of
![]() $T$
is isomorphic to
$T$
is isomorphic to
![]() $V(X_{0})\cup V(Y_{2},\ldots ,Y_{n})\subseteq \mathbb{P}(T_{1}^{\ast })$
. In particular, an
$V(X_{0})\cup V(Y_{2},\ldots ,Y_{n})\subseteq \mathbb{P}(T_{1}^{\ast })$
. In particular, an
![]() $X_{0}$
-torsionfree point module over
$X_{0}$
-torsionfree point module over
![]() $T$
must be annihilated by
$T$
must be annihilated by
![]() $Y_{2},\ldots ,Y_{n}$
.
$Y_{2},\ldots ,Y_{n}$
.
The point modules over
![]() $T$
that are annihilated by
$T$
that are annihilated by
![]() $Y_{2},\ldots ,Y_{n}$
are parameterized by
$Y_{2},\ldots ,Y_{n}$
are parameterized by
![]() $\mathbb{P}^{1}$
.
$\mathbb{P}^{1}$
.
Proof. The final statement comes directly from the isomorphism of
![]() $V$
with the Jordan plane (if
$V$
with the Jordan plane (if
![]() $a\neq 0$
) or with
$a\neq 0$
) or with
![]() $\Bbbk [X_{0},X_{1}]$
(if
$\Bbbk [X_{0},X_{1}]$
(if
![]() $a=0$
).
$a=0$
).
We multilinearize the relations of
![]() $T$
as in [Reference Artin, Tate and Van den BerghATVdB90], to compute the scheme
$T$
as in [Reference Artin, Tate and Van den BerghATVdB90], to compute the scheme
![]() $X(2)\subseteq \mathbb{P}(T_{1}^{\ast })^{\times 2}$
parameterizing truncated point modules over
$X(2)\subseteq \mathbb{P}(T_{1}^{\ast })^{\times 2}$
parameterizing truncated point modules over
![]() $T$
with Hilbert series
$T$
with Hilbert series
![]() $1+t+t^{2}$
. Let the coordinates on
$1+t+t^{2}$
. Let the coordinates on
![]() $\mathbb{P}(T_{1}^{\ast })^{\times 2}$
be
$\mathbb{P}(T_{1}^{\ast })^{\times 2}$
be
![]() $X_{0},X_{1},Y_{2},\ldots ,Y_{n},X_{0}^{\prime },X_{1}^{\prime },Y_{2}^{\prime },\ldots ,Y_{n}^{\prime }$
. We thus obtain an
$X_{0},X_{1},Y_{2},\ldots ,Y_{n},X_{0}^{\prime },X_{1}^{\prime },Y_{2}^{\prime },\ldots ,Y_{n}^{\prime }$
. We thus obtain an
![]() $\binom{n+1}{2}\times (n+1)$
matrix
$\binom{n+1}{2}\times (n+1)$
matrix
![]() $A$
with entries in
$A$
with entries in
![]() $T_{1}$
so that
$T_{1}$
so that
![]() $X(2)$
is defined by the equations
$X(2)$
is defined by the equations
 $$\begin{eqnarray}A\left[\begin{array}{@{}c@{}}X_{0}^{\prime }\\ X_{1}^{\prime }\\ Y_{2}^{\prime }\\ \vdots \\ Y_{n}^{\prime }\end{array}\right]=0.\end{eqnarray}$$
$$\begin{eqnarray}A\left[\begin{array}{@{}c@{}}X_{0}^{\prime }\\ X_{1}^{\prime }\\ Y_{2}^{\prime }\\ \vdots \\ Y_{n}^{\prime }\end{array}\right]=0.\end{eqnarray}$$
The rows of
![]() $A$
are given by:
$A$
are given by:
 $$\begin{eqnarray}\displaystyle & A:\quad \left[\begin{array}{@{}ccc@{}}X_{1}-aX_{0} & -X_{0} & 0\ldots \end{array}\right] & \displaystyle \nonumber\\ \displaystyle & A(k):\quad \left[\begin{array}{@{}ccccc@{}}0 & -Y_{k} & \ldots \, & X_{1}-(a+k)X_{0} & \ldots \\ & & & (k+1) & \end{array}\right] & \displaystyle \nonumber\\ \displaystyle & B(k):\quad \left[\begin{array}{@{}ccccc@{}}-Y_{k} & 0 & \ldots \, & X_{0} & \ldots \\ & & & (k+1) & \end{array}\right] & \displaystyle \nonumber\\ \displaystyle & C(j,k):\quad \left[\begin{array}{@{}cccccc@{}}0 & \ldots \, & Y_{k} & \ldots \, & -Y_{j} & \ldots \\ & & (j+1) & & (k+1)\end{array}\right]. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & A:\quad \left[\begin{array}{@{}ccc@{}}X_{1}-aX_{0} & -X_{0} & 0\ldots \end{array}\right] & \displaystyle \nonumber\\ \displaystyle & A(k):\quad \left[\begin{array}{@{}ccccc@{}}0 & -Y_{k} & \ldots \, & X_{1}-(a+k)X_{0} & \ldots \\ & & & (k+1) & \end{array}\right] & \displaystyle \nonumber\\ \displaystyle & B(k):\quad \left[\begin{array}{@{}ccccc@{}}-Y_{k} & 0 & \ldots \, & X_{0} & \ldots \\ & & & (k+1) & \end{array}\right] & \displaystyle \nonumber\\ \displaystyle & C(j,k):\quad \left[\begin{array}{@{}cccccc@{}}0 & \ldots \, & Y_{k} & \ldots \, & -Y_{j} & \ldots \\ & & (j+1) & & (k+1)\end{array}\right]. & \displaystyle \nonumber\end{eqnarray}$$
(Here we use
![]() $(\ell )$
to indicate the column of an entry.)
$(\ell )$
to indicate the column of an entry.)
Let
![]() $X^{\prime }$
be the projection of
$X^{\prime }$
be the projection of
![]() $X(2)$
onto the first coordinate. It is standard that
$X(2)$
onto the first coordinate. It is standard that
![]() $X^{\prime }$
is defined by the locus where
$X^{\prime }$
is defined by the locus where
![]() $\operatorname{rank}(A)<n+1$
. Consider the minor
$\operatorname{rank}(A)<n+1$
. Consider the minor
![]() $A_{k}$
of
$A_{k}$
of
![]() $A$
given by rows
$A$
given by rows
![]() $A,A(k),$
and
$A,A(k),$
and
![]() $B(2)-B(n)$
. In columns
$B(2)-B(n)$
. In columns
![]() $j\geqslant 2,j\neq k$
the only nonzero entry of
$j\geqslant 2,j\neq k$
the only nonzero entry of
![]() $A_{k}$
is the
$A_{k}$
is the
![]() $(j+1,j+1)$
entry
$(j+1,j+1)$
entry
![]() $X_{0}$
. Thus
$X_{0}$
. Thus
 $$\begin{eqnarray}\det A_{k}=\pm X_{0}^{n-2}\left|\begin{array}{@{}ccc@{}}X_{1}-aX_{0} & -X_{0} & 0\\ 0 & -Y_{k} & X_{1}-(a+k)X_{0}\\ -Y_{k} & 0 & X_{0}\end{array}\right|=\pm kX_{0}^{n}Y_{k}.\end{eqnarray}$$
$$\begin{eqnarray}\det A_{k}=\pm X_{0}^{n-2}\left|\begin{array}{@{}ccc@{}}X_{1}-aX_{0} & -X_{0} & 0\\ 0 & -Y_{k} & X_{1}-(a+k)X_{0}\\ -Y_{k} & 0 & X_{0}\end{array}\right|=\pm kX_{0}^{n}Y_{k}.\end{eqnarray}$$
Since
![]() $k\neq 0$
we have that
$k\neq 0$
we have that
![]() $X^{\prime }$
is a closed subscheme of
$X^{\prime }$
is a closed subscheme of
![]() $V(X_{1}^{n}Y_{2},\ldots ,X_{1}^{n}Y_{n})$
.
$V(X_{1}^{n}Y_{2},\ldots ,X_{1}^{n}Y_{n})$
.
Let
![]() $Y$
be the reduced point scheme of
$Y$
be the reduced point scheme of
![]() $T$
. Since
$T$
. Since
![]() $T$
is strongly Noetherian, for some
$T$
is strongly Noetherian, for some
![]() $N$
we have
$N$
we have
![]() $Y\subseteq \mathbb{P}(T_{1}^{\ast })^{\times N}$
. Let
$Y\subseteq \mathbb{P}(T_{1}^{\ast })^{\times N}$
. Let
![]() $X$
be the projection of
$X$
be the projection of
![]() $Y$
to the first factor; we have
$Y$
to the first factor; we have
![]() $X\subseteq X^{\prime }$
. To prove that this projection induces an isomorphism
$X\subseteq X^{\prime }$
. To prove that this projection induces an isomorphism
![]() $Y\cong V(X_{0})\cup V(Y_{2},\ldots ,Y_{n})$
it suffices to prove that each point of
$Y\cong V(X_{0})\cup V(Y_{2},\ldots ,Y_{n})$
it suffices to prove that each point of
![]() $V(X_{0})\cup V(Y_{2},\ldots ,Y_{n})$
corresponds to a point module. That is, if
$V(X_{0})\cup V(Y_{2},\ldots ,Y_{n})$
corresponds to a point module. That is, if
![]() $W$
is a codimension-1 subspace of
$W$
is a codimension-1 subspace of
![]() $T_{1}$
with either
$T_{1}$
with either
![]() $X_{0}\in W$
or
$X_{0}\in W$
or
![]() $Y_{2},\ldots ,Y_{n}\in W$
we must show that
$Y_{2},\ldots ,Y_{n}\in W$
we must show that
![]() $T/WT$
is a point module. If
$T/WT$
is a point module. If
![]() $X_{0}\in W$
then
$X_{0}\in W$
then
![]() $T/WT$
is isomorphic to the right module over
$T/WT$
is isomorphic to the right module over
![]() $T/X_{0}T$
defined by factoring out the image of
$T/X_{0}T$
defined by factoring out the image of
![]() $W$
. Since
$W$
. Since
![]() $T/X_{0}T$
is commutative any codimension-1 subspace of
$T/X_{0}T$
is commutative any codimension-1 subspace of
![]() $(T/X_{0}T)_{1}$
defines a point module, so
$(T/X_{0}T)_{1}$
defines a point module, so
![]() $T/WT$
is a point module over
$T/WT$
is a point module over
![]() $T$
.
$T$
.
Now suppose that
![]() $Y_{2},\ldots ,Y_{n}\in W$
. Then
$Y_{2},\ldots ,Y_{n}\in W$
. Then
![]() $T/WT$
is isomorphic to the right module over
$T/WT$
is isomorphic to the right module over
![]() $V$
given by factoring out the image of
$V$
given by factoring out the image of
![]() $W$
. As
$W$
. As
![]() $V$
is isomorphic either to the Jordan plane or to
$V$
is isomorphic either to the Jordan plane or to
![]() $\Bbbk [X_{0},X_{1}]$
, we see likewise that any codimension-1 subspace of
$\Bbbk [X_{0},X_{1}]$
, we see likewise that any codimension-1 subspace of
![]() $T_{1}$
that contains
$T_{1}$
that contains
![]() $Y_{2},\ldots ,Y_{n}$
defines a point module.◻
$Y_{2},\ldots ,Y_{n}$
defines a point module.◻
The natural map
![]() $T\rightarrow V$
induces a graded homomorphism
$T\rightarrow V$
induces a graded homomorphism
![]() $\unicode[STIX]{x1D701}:T[X_{0}^{-1}]\rightarrow D$
, where
$\unicode[STIX]{x1D701}:T[X_{0}^{-1}]\rightarrow D$
, where
![]() $D=Q_{gr}(V)=V[v^{-1}:v\in V\text{ is nonzero and homogeneous}]$
. Let
$D=Q_{gr}(V)=V[v^{-1}:v\in V\text{ is nonzero and homogeneous}]$
. Let
![]() $u=X_{1}X_{0}^{-1}$
and let
$u=X_{1}X_{0}^{-1}$
and let
![]() $t=X_{0}$
. It is well known that
$t=X_{0}$
. It is well known that
![]() $D\cong \Bbbk (u)[t,t^{-1};\unicode[STIX]{x1D70E}]$
, where
$D\cong \Bbbk (u)[t,t^{-1};\unicode[STIX]{x1D70E}]$
, where
![]() $\unicode[STIX]{x1D70E}(u)=u-a$
. To check this we verify that we have
$\unicode[STIX]{x1D70E}(u)=u-a$
. To check this we verify that we have
![]() $X_{1}X_{0}=ut^{2}=t(u+a)t=X_{0}(X_{1}+aX_{0})$
.
$X_{1}X_{0}=ut^{2}=t(u+a)t=X_{0}(X_{1}+aX_{0})$
.
Our next result computes
![]() $\unicode[STIX]{x1D701}(R)\subseteq \Bbbk (u)[t;\unicode[STIX]{x1D70E}]$
. To prove Theorem 6.1, the case
$\unicode[STIX]{x1D701}(R)\subseteq \Bbbk (u)[t;\unicode[STIX]{x1D70E}]$
. To prove Theorem 6.1, the case
![]() $a=0$
is the only one needed, but we give the general result because it is of independent interest.
$a=0$
is the only one needed, but we give the general result because it is of independent interest.
Proposition 6.6. We have
![]() $\unicode[STIX]{x1D701}(R)\cong V^{(n)}$
, the
$\unicode[STIX]{x1D701}(R)\cong V^{(n)}$
, the
![]() $n$
th Veronese of
$n$
th Veronese of
![]() $V$
.
$V$
.
Proof. Recall that
![]() $R=R(n,a)$
, where
$R=R(n,a)$
, where
![]() $n\geqslant 1$
. Note also that the subring of
$n\geqslant 1$
. Note also that the subring of
![]() $R$
generated by
$R$
generated by
![]() $X_{0},\ldots ,X_{k}$
is isomorphic to
$X_{0},\ldots ,X_{k}$
is isomorphic to
![]() $R(k,a)$
for all
$R(k,a)$
for all
![]() $1\leqslant k\leqslant n$
. We abuse notation and write
$1\leqslant k\leqslant n$
. We abuse notation and write
![]() $R(1,a)\subseteq R(2,a)\subseteq \cdots \subseteq R(n,a)$
, and use this to prove the theorem by induction on
$R(1,a)\subseteq R(2,a)\subseteq \cdots \subseteq R(n,a)$
, and use this to prove the theorem by induction on
![]() $n$
. Likewise, we write
$n$
. Likewise, we write
![]() $A(1,a)\subseteq A(n,a)$
.
$A(1,a)\subseteq A(n,a)$
.
We show, for all
![]() $k$
, that
$k$
, that
![]() $\unicode[STIX]{x1D701}(X_{k})\in k[u]\cdot t$
and, more specifically, that
$\unicode[STIX]{x1D701}(X_{k})\in k[u]\cdot t$
and, more specifically, that
We need a subsidiary lemma. Recall that the underlying space of
![]() $R$
is the commutative ring
$R$
is the commutative ring
![]() $A$
, with multiplication indicated by
$A$
, with multiplication indicated by
![]() $\ast$
in
$\ast$
in
![]() $R$
and juxtaposition in
$R$
and juxtaposition in
![]() $A$
. When we write an expression like
$A$
. When we write an expression like
![]() $X_{1}^{j}$
, we mean the commutative power; we write
$X_{1}^{j}$
, we mean the commutative power; we write
![]() $X_{1}^{\ast j}$
to mean the noncommutative power.
$X_{1}^{\ast j}$
to mean the noncommutative power.
Lemma 6.8. For
![]() $0\leqslant k\leqslant n$
, the following hold.
$0\leqslant k\leqslant n$
, the following hold.
(1) For any
 $f\in R(1,a)$
, we have
$f\in R(1,a)$
, we have  $$\begin{eqnarray}X_{k}\ast f-X_{k}f\in \mathop{\sum }_{i=0}^{k-1}X_{i}\ast R(1,a)=\mathop{\sum }_{i=0}^{k-1}X_{i}A(1,a).\end{eqnarray}$$
$$\begin{eqnarray}X_{k}\ast f-X_{k}f\in \mathop{\sum }_{i=0}^{k-1}X_{i}\ast R(1,a)=\mathop{\sum }_{i=0}^{k-1}X_{i}A(1,a).\end{eqnarray}$$
(2)
 $$\begin{eqnarray}\mathop{\sum }_{i=0}^{k}X_{i}\ast R(1,a)=\mathop{\sum }_{i=0}^{k}X_{i}A(1,a).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=0}^{k}X_{i}\ast R(1,a)=\mathop{\sum }_{i=0}^{k}X_{i}A(1,a).\end{eqnarray}$$
Proof. Again, we induct on
![]() $k$
; the result is trivial for
$k$
; the result is trivial for
![]() $k=0$
. Assume we know the result for
$k=0$
. Assume we know the result for
![]() $k$
.
$k$
.
![]() $(1)$
We may assume that
$(1)$
We may assume that
![]() $f$
is
$f$
is
![]() $e$
-homogeneous. We have
$e$
-homogeneous. We have
Each
![]() $X_{k+1-i}\binom{\unicode[STIX]{x1D6E4}}{i}(f)$
is a scalar multiple of
$X_{k+1-i}\binom{\unicode[STIX]{x1D6E4}}{i}(f)$
is a scalar multiple of
![]() $X_{k+1-i}f$
. Thus the right-hand side is in
$X_{k+1-i}f$
. Thus the right-hand side is in
![]() $\sum _{i=0}^{k}X_{i}A(1,a)=\sum _{i=0}^{k}X_{i}\ast R(1,a)$
by induction.
$\sum _{i=0}^{k}X_{i}A(1,a)=\sum _{i=0}^{k}X_{i}\ast R(1,a)$
by induction.
![]() $(2)$
follows directly from
$(2)$
follows directly from
![]() $(1)$
.◻
$(1)$
.◻
Since
![]() $\unicode[STIX]{x1D701}(X_{0}),\unicode[STIX]{x1D701}(X_{1})\in \Bbbk [u][t;\unicode[STIX]{x1D70E}]$
we obtain that
$\unicode[STIX]{x1D701}(X_{0}),\unicode[STIX]{x1D701}(X_{1})\in \Bbbk [u][t;\unicode[STIX]{x1D70E}]$
we obtain that
![]() $\unicode[STIX]{x1D701}(R(1,a))\subseteq \Bbbk [u][t;\unicode[STIX]{x1D70E}]$
.
$\unicode[STIX]{x1D701}(R(1,a))\subseteq \Bbbk [u][t;\unicode[STIX]{x1D70E}]$
.
Since
![]() $\unicode[STIX]{x1D701}$
is graded, we have
$\unicode[STIX]{x1D701}$
is graded, we have
![]() $\unicode[STIX]{x1D701}(X_{1}^{j})=f_{j}(u)t^{j}$
. We have
$\unicode[STIX]{x1D701}(X_{1}^{j})=f_{j}(u)t^{j}$
. We have
![]() $\unicode[STIX]{x1D701}(X_{1}^{\ast j})=(ut)^{j}=u(u-a)(u-2a)\cdots (u-(j-1)a)t^{j}$
, which has leading term
$\unicode[STIX]{x1D701}(X_{1}^{\ast j})=(ut)^{j}=u(u-a)(u-2a)\cdots (u-(j-1)a)t^{j}$
, which has leading term
![]() $u^{j}t^{j}$
. We immediately obtain from Lemma 6.8(1) (and an elementary induction) that
$u^{j}t^{j}$
. We immediately obtain from Lemma 6.8(1) (and an elementary induction) that
Assume now that we have shown that (6.7) holds for
![]() $0,\ldots ,k-1$
, and consider the image of
$0,\ldots ,k-1$
, and consider the image of
![]() $X_{0}^{k}X_{k}=X_{0}^{\ast (k)}\ast X_{k}$
under
$X_{0}^{k}X_{k}=X_{0}^{\ast (k)}\ast X_{k}$
under
![]() $\unicode[STIX]{x1D701}$
. Recall that
$\unicode[STIX]{x1D701}$
. Recall that
Thus
 $$\begin{eqnarray}\unicode[STIX]{x1D701}(X_{0}^{k}X_{k})=\unicode[STIX]{x1D701}\left(X_{0}^{k}Y_{k}+\mathop{\sum }_{p=1}^{k}\frac{(-1)^{p+1}X_{0}^{k-p}X_{k-p}X_{1}^{p}}{p!}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}(X_{0}^{k}X_{k})=\unicode[STIX]{x1D701}\left(X_{0}^{k}Y_{k}+\mathop{\sum }_{p=1}^{k}\frac{(-1)^{p+1}X_{0}^{k-p}X_{k-p}X_{1}^{p}}{p!}\right).\end{eqnarray}$$
We know that
![]() $\unicode[STIX]{x1D701}(X_{0}^{k}Y_{k})=0$
since
$\unicode[STIX]{x1D701}(X_{0}^{k}Y_{k})=0$
since
![]() $\unicode[STIX]{x1D701}(Y_{k})=0$
. Applying (6.7), Lemma 6.8(1), and (6.9), we obtain that
$\unicode[STIX]{x1D701}(Y_{k})=0$
. Applying (6.7), Lemma 6.8(1), and (6.9), we obtain that
Thus (6.10) reduces to
 $$\begin{eqnarray}\unicode[STIX]{x1D701}(X_{0}^{k}X_{k})=\left(\left(\mathop{\sum }_{p=1}^{k}\frac{(-1)^{p+1}}{p!(k-p)!}\right)u^{k}+\text{lower terms}\right)t^{k+1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}(X_{0}^{k}X_{k})=\left(\left(\mathop{\sum }_{p=1}^{k}\frac{(-1)^{p+1}}{p!(k-p)!}\right)u^{k}+\text{lower terms}\right)t^{k+1}.\end{eqnarray}$$
Since commuting with
![]() $t$
does not effect the leading term of a polynomial in
$t$
does not effect the leading term of a polynomial in
![]() $u$
, it follows that
$u$
, it follows that
 $$\begin{eqnarray}\unicode[STIX]{x1D701}(X_{k})=t^{-k}\unicode[STIX]{x1D701}(X_{0}^{k}X_{k})=\left(\left(\mathop{\sum }_{p=1}^{k}\frac{(-1)^{p+1}}{p!(k-p)!}\right)u^{k}+\text{lower terms}\right)t,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}(X_{k})=t^{-k}\unicode[STIX]{x1D701}(X_{0}^{k}X_{k})=\left(\left(\mathop{\sum }_{p=1}^{k}\frac{(-1)^{p+1}}{p!(k-p)!}\right)u^{k}+\text{lower terms}\right)t,\end{eqnarray}$$
and that
![]() $\unicode[STIX]{x1D701}(X_{k})t^{-1}\in \Bbbk [u]$
. Finally,
$\unicode[STIX]{x1D701}(X_{k})t^{-1}\in \Bbbk [u]$
. Finally,
as needed. We have thus established (6.7) for
![]() $X_{k}$
.
$X_{k}$
.
It follows from (6.7) that
for all
![]() $k$
.
$k$
.
To complete the proof of the proposition, we must identify the ring
![]() $S=\unicode[STIX]{x1D701}(R)=\Bbbk \langle t,ut,\ldots ,u^{n}t\rangle \subseteq \Bbbk (u)[t;\unicode[STIX]{x1D70E}_{a}]$
. Denoting the point
$S=\unicode[STIX]{x1D701}(R)=\Bbbk \langle t,ut,\ldots ,u^{n}t\rangle \subseteq \Bbbk (u)[t;\unicode[STIX]{x1D70E}_{a}]$
. Denoting the point
![]() $[1:0]\in \mathbb{P}^{1}$
by
$[1:0]\in \mathbb{P}^{1}$
by
![]() $\infty$
, we may identify
$\infty$
, we may identify
![]() $S_{1}$
with global sections of the sheaf
$S_{1}$
with global sections of the sheaf
![]() ${\mathcal{O}}_{\mathbb{P}^{1}}(n\infty )$
, multiplied by
${\mathcal{O}}_{\mathbb{P}^{1}}(n\infty )$
, multiplied by
![]() $t$
. It is then clear that
$t$
. It is then clear that
![]() $S$
is isomorphic to the
$S$
is isomorphic to the
![]() $n$
th Veronese of the twisted homogeneous coordinate ring (see [Reference Artin and Van den BerghAVdB90])
$n$
th Veronese of the twisted homogeneous coordinate ring (see [Reference Artin and Van den BerghAVdB90])
![]() $B(\mathbb{P}^{1},{\mathcal{O}}(1),\unicode[STIX]{x1D70E}_{a/n})$
. We have that
$B(\mathbb{P}^{1},{\mathcal{O}}(1),\unicode[STIX]{x1D70E}_{a/n})$
. We have that
![]() $B(\mathbb{P}^{1},{\mathcal{O}}(1),\unicode[STIX]{x1D70E}_{a/n})$
is isomorphic to the Jordan plane if
$B(\mathbb{P}^{1},{\mathcal{O}}(1),\unicode[STIX]{x1D70E}_{a/n})$
is isomorphic to the Jordan plane if
![]() $a\neq 0$
and to
$a\neq 0$
and to
![]() $\Bbbk [X_{0},X_{1}]$
if
$\Bbbk [X_{0},X_{1}]$
if
![]() $a=0$
by [Reference RogalskiRog14, Example 4.13]. Thus, no matter the value of
$a=0$
by [Reference RogalskiRog14, Example 4.13]. Thus, no matter the value of
![]() $a$
we have
$a$
we have
![]() $S\cong V^{(n)}$
.◻
$S\cong V^{(n)}$
.◻
Note that we have constructed above the homomorphism
![]() $R(n,a)\rightarrow R(1,a/n)^{(n)}$
that was predicted at the end of Section 2. Taking associated graded rings, we obtain also the predicted Poisson homomorphism
$R(n,a)\rightarrow R(1,a/n)^{(n)}$
that was predicted at the end of Section 2. Taking associated graded rings, we obtain also the predicted Poisson homomorphism
![]() $A(n,a)\rightarrow A(1,a/n)^{(n)}$
. Further, if we let
$A(n,a)\rightarrow A(1,a/n)^{(n)}$
. Further, if we let
![]() $1\leqslant k\leqslant n$
, then factoring out
$1\leqslant k\leqslant n$
, then factoring out
![]() $X_{0},\ldots ,X_{n-k}$
and applying this construction to the factor we obtain a surjection
$X_{0},\ldots ,X_{n-k}$
and applying this construction to the factor we obtain a surjection
![]() $R(n,a)\rightarrow R(1,(a+n-k)/k)^{(k)}$
and thus a
$R(n,a)\rightarrow R(1,(a+n-k)/k)^{(k)}$
and thus a
![]() $\mathbb{P}^{1}$
of point modules corresponding to point modules of
$\mathbb{P}^{1}$
of point modules corresponding to point modules of
![]() $R(1,(a+n-k)/k)$
. These modules are all predicted by the discussion in Section 2. In a sense the striking content of Theorem 6.1 is that there are no other point modules for
$R(1,(a+n-k)/k)$
. These modules are all predicted by the discussion in Section 2. In a sense the striking content of Theorem 6.1 is that there are no other point modules for
![]() $R(n,a)$
.
$R(n,a)$
.
We now prove Theorem 6.1.
Proof of Theorem 6.1.
By Theorem 5.4, it suffices to prove the result for right point modules. We prove the result by induction on
![]() $n$
, first noting the result is trivial for
$n$
, first noting the result is trivial for
![]() $n=1$
, since point modules over
$n=1$
, since point modules over
![]() $R=R(1,a)$
are in bijection with codimension-1 subspaces of
$R=R(1,a)$
are in bijection with codimension-1 subspaces of
![]() $R_{1}$
for any
$R_{1}$
for any
![]() $a$
. Thus we may suppose that
$a$
. Thus we may suppose that
![]() $n>1$
. Since
$n>1$
. Since
![]() $R(n,a)$
is a Zhang twist of
$R(n,a)$
is a Zhang twist of
![]() $R(n,0)$
(Theorem 4.2), by [Reference ZhangZha96] it suffices to prove the result for
$R(n,0)$
(Theorem 4.2), by [Reference ZhangZha96] it suffices to prove the result for
![]() $R=R(n,0)$
.
$R=R(n,0)$
.
Let
![]() $M=R/J$
be a point module, and recall the definition of the homomorphism
$M=R/J$
be a point module, and recall the definition of the homomorphism
![]() $\unicode[STIX]{x1D701}$
from just before Proposition 6.6. We claim that
$\unicode[STIX]{x1D701}$
from just before Proposition 6.6. We claim that
![]() $J=J_{1}R$
. If
$J=J_{1}R$
. If
![]() $X_{0}\not \in J$
then by Lemma 6.3
$X_{0}\not \in J$
then by Lemma 6.3
![]() $M$
is
$M$
is
![]() $X_{0}$
-torsionfree and by Proposition 6.4,
$X_{0}$
-torsionfree and by Proposition 6.4,
![]() $M$
is also an
$M$
is also an
![]() $X_{0}$
-torsionfree
$X_{0}$
-torsionfree
![]() $T$
-point module. Thus
$T$
-point module. Thus
![]() $MY_{k}=0$
for
$MY_{k}=0$
for
![]() $k\in \{2,\ldots ,n\}$
by Proposition 6.2, so
$k\in \{2,\ldots ,n\}$
by Proposition 6.2, so
![]() $M$
is annihilated by
$M$
is annihilated by
![]() $\ker \unicode[STIX]{x1D701}$
. By Proposition 6.6,
$\ker \unicode[STIX]{x1D701}$
. By Proposition 6.6,
![]() $R/\ker \unicode[STIX]{x1D701}$
is isomorphic to
$R/\ker \unicode[STIX]{x1D701}$
is isomorphic to
![]() $\Bbbk [X,Y]^{(n)}$
. The claim follows from the fact that if
$\Bbbk [X,Y]^{(n)}$
. The claim follows from the fact that if
![]() $J$
is a right ideal of
$J$
is a right ideal of
![]() $\Bbbk [X,Y]^{(n)}$
such that
$\Bbbk [X,Y]^{(n)}$
such that
![]() $(\Bbbk [X,Y]^{(n)})/J$
is a point module, then
$(\Bbbk [X,Y]^{(n)})/J$
is a point module, then
![]() $J$
is generated in degree one.
$J$
is generated in degree one.
We may thus view the point scheme
![]() $X$
of
$X$
of
![]() $R$
as contained in
$R$
as contained in
![]() $\mathbb{P}(R_{1}^{\ast })$
, where
$\mathbb{P}(R_{1}^{\ast })$
, where
![]() $M=R/J$
corresponds to the codimension-1 subspace
$M=R/J$
corresponds to the codimension-1 subspace
![]() $J_{1}\subseteq R_{1}$
. By slight abuse of notation, we regard a point module
$J_{1}\subseteq R_{1}$
. By slight abuse of notation, we regard a point module
![]() $M$
as a closed point of the point scheme
$M$
as a closed point of the point scheme
![]() $X\subseteq \mathbb{P}(R_{1}^{\ast })$
. Let
$X\subseteq \mathbb{P}(R_{1}^{\ast })$
. Let
![]() $Z(1)$
be the Zariski closure of
$Z(1)$
be the Zariski closure of
![]() $\{M=R/J~|~X_{0}\not \in J\}$
. Then
$\{M=R/J~|~X_{0}\not \in J\}$
. Then
![]() $\ker \unicode[STIX]{x1D701}\subseteq J$
for all
$\ker \unicode[STIX]{x1D701}\subseteq J$
for all
![]() $M=R/J$
in
$M=R/J$
in
![]() $Z(1)$
. Thus
$Z(1)$
. Thus
![]() $Z(1)$
is isomorphic to the point scheme of
$Z(1)$
is isomorphic to the point scheme of
![]() $R/\ker \unicode[STIX]{x1D701}\cong \Bbbk [X,Y]^{(n)}$
, which is the image of the degree
$R/\ker \unicode[STIX]{x1D701}\cong \Bbbk [X,Y]^{(n)}$
, which is the image of the degree
![]() $n$
Veronese map from
$n$
Veronese map from
![]() $\mathbb{P}^{1}\rightarrow \mathbb{P}^{n}$
; in other words, a degree
$\mathbb{P}^{1}\rightarrow \mathbb{P}^{n}$
; in other words, a degree
![]() $n$
rational normal curve in
$n$
rational normal curve in
![]() $\mathbb{P}(\Bbbk [X,Y]_{n}^{\ast })=\mathbb{P}(R_{1}^{\ast })$
.
$\mathbb{P}(\Bbbk [X,Y]_{n}^{\ast })=\mathbb{P}(R_{1}^{\ast })$
.
It remains to consider the case of point modules annihilated by
![]() $X_{0}$
. By induction (using Proposition 3.7 as usual), these form a bouquet of
$X_{0}$
. By induction (using Proposition 3.7 as usual), these form a bouquet of
![]() $n-1$
rational normal curves in
$n-1$
rational normal curves in
![]() $V(X_{0})$
, and the result follows.◻
$V(X_{0})$
, and the result follows.◻
Remark 6.12. Let
![]() $a,b\in \Bbbk$
, and let
$a,b\in \Bbbk$
, and let
![]() $\unicode[STIX]{x1D719}_{b}$
be the automorphism of
$\unicode[STIX]{x1D719}_{b}$
be the automorphism of
![]() $R(n,a)$
defined in Lemma 4.3. It is easy to see that
$R(n,a)$
defined in Lemma 4.3. It is easy to see that
![]() $\unicode[STIX]{x1D719}_{b}$
extends to an automorphism of
$\unicode[STIX]{x1D719}_{b}$
extends to an automorphism of
![]() $R(n,a)[X_{0}^{-1}]=:R^{\circ }(n,a)$
. By Corollary 4.7, we have
$R(n,a)[X_{0}^{-1}]=:R^{\circ }(n,a)$
. By Corollary 4.7, we have
![]() $^{\unicode[STIX]{x1D719}_{b}}R^{\circ }(n,a)\cong R^{\circ }(n,a+b)$
. Let
$^{\unicode[STIX]{x1D719}_{b}}R^{\circ }(n,a)\cong R^{\circ }(n,a+b)$
. Let
![]() $\ast _{a}$
denote multiplication in
$\ast _{a}$
denote multiplication in
![]() $R(n,a)$
. Since
$R(n,a)$
. Since
![]() $[X_{0},Y_{k}]=0$
in
$[X_{0},Y_{k}]=0$
in
![]() $R^{\circ }(n,a+b)$
, we have
$R^{\circ }(n,a+b)$
, we have
so
![]() $\unicode[STIX]{x1D719}_{b}(Y_{k})=Y_{k}$
. It follows that
$\unicode[STIX]{x1D719}_{b}(Y_{k})=Y_{k}$
. It follows that
![]() $\ker \unicode[STIX]{x1D701}$
is
$\ker \unicode[STIX]{x1D701}$
is
![]() $\unicode[STIX]{x1D719}_{b}$
-invariant. One can use this to give an alternate proof of the
$\unicode[STIX]{x1D719}_{b}$
-invariant. One can use this to give an alternate proof of the
![]() $X_{0}$
-torsionfree case of Theorem 6.1.
$X_{0}$
-torsionfree case of Theorem 6.1.
7 Primes of
 $R$
and Poisson primes of
$R$
and Poisson primes of
 $A$
$A$
The results of the previous section construct surjections from
![]() $R(n,a)$
to
$R(n,a)$
to
![]() $R(1,a^{\prime })^{(n-k)}$
for all
$R(1,a^{\prime })^{(n-k)}$
for all
![]() $0\leqslant k<n$
(where
$0\leqslant k<n$
(where
![]() $a^{\prime }$
depends on
$a^{\prime }$
depends on
![]() $a$
,
$a$
,
![]() $n$
, and
$n$
, and
![]() $k$
). The kernels of these maps are of course prime ideals, and are in some sense independent of
$k$
). The kernels of these maps are of course prime ideals, and are in some sense independent of
![]() $a$
: for example, the kernel of the map
$a$
: for example, the kernel of the map
![]() $R(n,a)\rightarrow R(1,a/n)^{(n)}$
is generated by
$R(n,a)\rightarrow R(1,a/n)^{(n)}$
is generated by
![]() $Y_{2},\ldots ,Y_{n}$
no matter the value of
$Y_{2},\ldots ,Y_{n}$
no matter the value of
![]() $a$
. (This is a slight abuse of notation, since
$a$
. (This is a slight abuse of notation, since
![]() $Y_{2},\ldots ,Y_{n}$
are in the localization
$Y_{2},\ldots ,Y_{n}$
are in the localization
![]() $R(n,a)[X_{0}^{-1}]$
.) We see that, similar to the above, the
$R(n,a)[X_{0}^{-1}]$
.) We see that, similar to the above, the
![]() $d$
-graded prime spectrum of
$d$
-graded prime spectrum of
![]() $R(n,a)$
is largely independent of
$R(n,a)$
is largely independent of
![]() $a$
. On the other hand, the ungraded primes of
$a$
. On the other hand, the ungraded primes of
![]() $R(n,a)$
depends very sensitively on
$R(n,a)$
depends very sensitively on
![]() $a$
.
$a$
.
First, though, we explore the connection between primes of
![]() $R(n,a)$
and Poisson primes of
$R(n,a)$
and Poisson primes of
![]() $A(n,a)$
. It is well known that there is often a close relationship between prime ideals of a noncommutative ring
$A(n,a)$
. It is well known that there is often a close relationship between prime ideals of a noncommutative ring
![]() $R$
and Poisson primes of its semiclassical limit. Fix
$R$
and Poisson primes of its semiclassical limit. Fix
![]() $n$
and
$n$
and
![]() $a$
and let
$a$
and let
![]() $R=R(n,a)$
with multiplication
$R=R(n,a)$
with multiplication
![]() $\ast _{a}$
. Let
$\ast _{a}$
. Let
![]() $A=A(n,a)$
with Poisson bracket
$A=A(n,a)$
with Poisson bracket
![]() $\{-,-\}_{a}$
. We show that
$\{-,-\}_{a}$
. We show that
![]() $\operatorname{Spec}R=\operatorname{PSpec}A$
in the strongest possible sense. That is, we prove:
$\operatorname{Spec}R=\operatorname{PSpec}A$
in the strongest possible sense. That is, we prove:
Theorem 7.1. Let
![]() $P\subseteq A=R$
. Then:
$P\subseteq A=R$
. Then:
(1)
 $P\in \operatorname{Spec}R$
if and only if
$P\in \operatorname{Spec}R$
if and only if
 $P\in \operatorname{PSpec}A$
, and further every prime ideal of
$P\in \operatorname{PSpec}A$
, and further every prime ideal of
 $R$
is completely prime;
$R$
is completely prime;(2)
 $P$
is a primitive ideal of
$P$
is a primitive ideal of
 $R$
if and only if
$R$
if and only if
 $P$
is a Poisson primitive ideal of
$P$
is a Poisson primitive ideal of
 $A$
.
$A$
.
In the statement of Theorem 7.1, recall that an ideal
![]() $I$
of a ring
$I$
of a ring
![]() $R$
is called left (respectively right) primitive if it is the annihilator of a simple left (respectively right)
$R$
is called left (respectively right) primitive if it is the annihilator of a simple left (respectively right)
![]() $R$
-module. Thanks to Theorem 5.4 the two notions coincide for the ring
$R$
-module. Thanks to Theorem 5.4 the two notions coincide for the ring
![]() $R(n,a)$
and we do not specify left or right for a primitive ideal in this article. An ideal
$R(n,a)$
and we do not specify left or right for a primitive ideal in this article. An ideal
![]() $P$
of a Poisson ideal
$P$
of a Poisson ideal
![]() $A$
is called Poisson primitive if it is the largest Poisson ideal contained in a maximal ideal of the commutative ring
$A$
is called Poisson primitive if it is the largest Poisson ideal contained in a maximal ideal of the commutative ring
![]() $A$
.
$A$
.
We further give a stratification of
![]() $\operatorname{Spec}R=\operatorname{PSpec}A$
, and show the strata are homeomorphic to commutative (projective, projective-over-affine, or affine) varieties. We compute also the
$\operatorname{Spec}R=\operatorname{PSpec}A$
, and show the strata are homeomorphic to commutative (projective, projective-over-affine, or affine) varieties. We compute also the
![]() $d$
-homogeneous primes of
$d$
-homogeneous primes of
![]() $R$
, and show that (if
$R$
, and show that (if
![]() $a\not \in \mathbb{Z}$
) they do not depend on the precise value of
$a\not \in \mathbb{Z}$
) they do not depend on the precise value of
![]() $a$
.
$a$
.
Jordan’s work [Reference JordanJor14] on Poisson algebras and Ore extensions is crucial to this section. The following is a slight strengthening of [Reference JordanJor14, Theorem 3.6].
Proposition 7.2. Let
![]() $B$
be a Noetherian
$B$
be a Noetherian
![]() $\Bbbk$
-algebra that is a domain and let
$\Bbbk$
-algebra that is a domain and let
![]() $\unicode[STIX]{x1D6FF}$
be a nonzero derivation of
$\unicode[STIX]{x1D6FF}$
be a nonzero derivation of
![]() $B$
. Let
$B$
. Let
![]() $R=B[z;\unicode[STIX]{x1D6FF}]$
, which we write as the left
$R=B[z;\unicode[STIX]{x1D6FF}]$
, which we write as the left
![]() $B$
-module
$B$
-module
![]() $R=\bigoplus _{n\geqslant 0}Bz^{n}$
, with multiplication
$R=\bigoplus _{n\geqslant 0}Bz^{n}$
, with multiplication
![]() $\ast$
such that
$\ast$
such that
Let
![]() $A$
be the Poisson–Ore extension
$A$
be the Poisson–Ore extension
![]() $(B[z],\{-,-\}_{\unicode[STIX]{x1D6FF}})$
(see [Reference JordanJor14, Lemma 3.1]); as a ring
$(B[z],\{-,-\}_{\unicode[STIX]{x1D6FF}})$
(see [Reference JordanJor14, Lemma 3.1]); as a ring
![]() $A=B[z]$
, with Poisson bracket defined by
$A=B[z]$
, with Poisson bracket defined by
Let
![]() $P\subseteq R=A$
. Then:
$P\subseteq R=A$
. Then:
![]() $P\in \operatorname{Spec}R$
if and only if
$P\in \operatorname{Spec}R$
if and only if
![]() $P\in \operatorname{PSpec}A$
. Further, if
$P\in \operatorname{PSpec}A$
. Further, if
![]() $P\in \operatorname{Spec}R=\operatorname{PSpec}A$
, then either
$P\in \operatorname{Spec}R=\operatorname{PSpec}A$
, then either
![]() $P\supseteq \unicode[STIX]{x1D6FF}(B)$
or
$P\supseteq \unicode[STIX]{x1D6FF}(B)$
or
![]() $P$
is generated by the
$P$
is generated by the
![]() $\unicode[STIX]{x1D6FF}$
-invariant prime ideal
$\unicode[STIX]{x1D6FF}$
-invariant prime ideal
![]() $P\cap B$
of
$P\cap B$
of
![]() $B$
.
$B$
.
For the proof of Proposition 7.2, recall that a
![]() $\unicode[STIX]{x1D6FF}$
-ideal
$\unicode[STIX]{x1D6FF}$
-ideal
![]() $I$
of
$I$
of
![]() $B$
is an ideal
$B$
is an ideal
![]() $I$
with
$I$
with
![]() $\unicode[STIX]{x1D6FF}(I)\subset I$
. The
$\unicode[STIX]{x1D6FF}(I)\subset I$
. The
![]() $\unicode[STIX]{x1D6FF}$
-ideal
$\unicode[STIX]{x1D6FF}$
-ideal
![]() $I$
is
$I$
is
![]() $\unicode[STIX]{x1D6FF}$
-prime if for all
$\unicode[STIX]{x1D6FF}$
-prime if for all
![]() $\unicode[STIX]{x1D6FF}$
-ideals
$\unicode[STIX]{x1D6FF}$
-ideals
![]() $J,K$
of
$J,K$
of
![]() $B$
, we have that
$B$
, we have that
![]() $JK\subseteq I$
implies that
$JK\subseteq I$
implies that
![]() $J\subseteq I$
or
$J\subseteq I$
or
![]() $K\subseteq I$
. Since
$K\subseteq I$
. Since
![]() $\operatorname{char}\Bbbk =0$
, a
$\operatorname{char}\Bbbk =0$
, a
![]() $\unicode[STIX]{x1D6FF}$
-prime ideal of
$\unicode[STIX]{x1D6FF}$
-prime ideal of
![]() $B$
is prime by [Reference GoodearlGoo06, Lemma 1.1].
$B$
is prime by [Reference GoodearlGoo06, Lemma 1.1].
Proof of Proposition 7.2.
This proof is largely a recapitulation of the proof of [Reference JordanJor14, Theorem 3.6], pointing out that the homeomorphism constructed there is in fact the identity map. Let
![]() $J=\unicode[STIX]{x1D6FF}(B)B$
. For any
$J=\unicode[STIX]{x1D6FF}(B)B$
. For any
![]() $\unicode[STIX]{x1D6FF}$
-ideal
$\unicode[STIX]{x1D6FF}$
-ideal
![]() $Q$
of
$Q$
of
![]() $B$
, we have
$B$
, we have
![]() $Q\ast R=R\ast Q=QA=Q[z]$
(using the identification of
$Q\ast R=R\ast Q=QA=Q[z]$
(using the identification of
![]() $R$
with
$R$
with
![]() $A$
as left
$A$
as left
![]() $B$
-modules). In particular, this holds for
$B$
-modules). In particular, this holds for
![]() $Q=J$
.
$Q=J$
.
Let
![]() $P\subseteq A=R$
and suppose that either
$P\subseteq A=R$
and suppose that either
![]() $P\in \operatorname{Spec}R$
or
$P\in \operatorname{Spec}R$
or
![]() $P\in \operatorname{PSpec}A$
. If
$P\in \operatorname{PSpec}A$
. If
![]() $J\subseteq P$
then
$J\subseteq P$
then
![]() $P\supseteq JA=J\ast R=R\ast J$
. From (7.3), the two multiplications on the graded vector space
$P\supseteq JA=J\ast R=R\ast J$
. From (7.3), the two multiplications on the graded vector space
![]() $A/JA=R/J\ast R$
are equal, and the induced Poisson bracket on
$A/JA=R/J\ast R$
are equal, and the induced Poisson bracket on
![]() $A/JA$
is trivial. Let
$A/JA$
is trivial. Let
![]() $C=R/J\ast R=A/JA$
. Then
$C=R/J\ast R=A/JA$
. Then
![]() $J\subseteq P\in \operatorname{Spec}R$
holds if and only if
$J\subseteq P\in \operatorname{Spec}R$
holds if and only if
![]() $P/J\ast R=P/JA\in \operatorname{Spec}C=\operatorname{PSpec}C$
, if and only if
$P/J\ast R=P/JA\in \operatorname{Spec}C=\operatorname{PSpec}C$
, if and only if
![]() $J\subseteq P\in \operatorname{PSpec}A$
.
$J\subseteq P\in \operatorname{PSpec}A$
.
Now suppose that
![]() $J\not \subseteq P$
and let
$J\not \subseteq P$
and let
![]() $Q=P\cap B$
; note
$Q=P\cap B$
; note
![]() $Q$
is a
$Q$
is a
![]() $\unicode[STIX]{x1D6FF}$
-prime ideal of
$\unicode[STIX]{x1D6FF}$
-prime ideal of
![]() $B$
. By [Reference JordanJor14, Lemma 3.2], if
$B$
. By [Reference JordanJor14, Lemma 3.2], if
![]() $P\in \operatorname{PSpec}A$
then
$P\in \operatorname{PSpec}A$
then
![]() $P=QA=Q\ast R$
, and thus
$P=QA=Q\ast R$
, and thus
![]() $P\in \operatorname{Spec}R$
. But by [Reference JordanJor14, Lemma 3.3], if
$P\in \operatorname{Spec}R$
. But by [Reference JordanJor14, Lemma 3.3], if
![]() $P\in \operatorname{Spec}R$
then
$P\in \operatorname{Spec}R$
then
![]() $P=Q\ast R=QA$
and
$P=Q\ast R=QA$
and
![]() $P\in \operatorname{PSpec}A$
.
$P\in \operatorname{PSpec}A$
.
Finally, we note that the results in [Reference JordanJor14] are stated for
![]() $\Bbbk =\mathbb{C}$
, but are valid over any field of characteristic 0.◻
$\Bbbk =\mathbb{C}$
, but are valid over any field of characteristic 0.◻
We now prove Theorem 7.1. Recall from Section 3 that
![]() $R^{\circ }=R[X_{0}^{-1}]$
and
$R^{\circ }=R[X_{0}^{-1}]$
and
![]() $A^{\circ }=A[X_{0}^{-1}]$
.
$A^{\circ }=A[X_{0}^{-1}]$
.
Proof of Theorem 7.1.
![]() $(1)$
If
$(1)$
If
![]() $n=1$
the result is well known. So let
$n=1$
the result is well known. So let
![]() $n>1$
and let
$n>1$
and let
![]() $P\subseteq A=R$
.
$P\subseteq A=R$
.
First suppose that
![]() $X_{0}\not \in P$
. Let
$X_{0}\not \in P$
. Let
![]() $P^{\circ }:=P[X_{0}^{-1}]=P+X_{0}^{-1}P+\cdots \subseteq A^{\circ }=R^{\circ }$
. If
$P^{\circ }:=P[X_{0}^{-1}]=P+X_{0}^{-1}P+\cdots \subseteq A^{\circ }=R^{\circ }$
. If
![]() $P\in \operatorname{Spec}R$
or
$P\in \operatorname{Spec}R$
or
![]() $P\in \operatorname{PSpec}A$
then
$P\in \operatorname{PSpec}A$
then
![]() $P=P^{\circ }\cap A$
. So it suffices to prove that
$P=P^{\circ }\cap A$
. So it suffices to prove that
![]() $P^{\circ }\in \operatorname{Spec}R^{\circ }$
$P^{\circ }\in \operatorname{Spec}R^{\circ }$
![]() $\;\Longleftrightarrow \;$
$\;\Longleftrightarrow \;$
![]() $P^{\circ }\in \operatorname{PSpec}A^{\circ }$
. This is an immediate application of Lemma 3.26 and Proposition 7.2. That prime ideals of
$P^{\circ }\in \operatorname{PSpec}A^{\circ }$
. This is an immediate application of Lemma 3.26 and Proposition 7.2. That prime ideals of
![]() $R^{\circ }$
are completely prime is shown in [Reference SigurdssonSig84] (see also [Reference JordanJor14, Remark 3.7]) and the rest of
$R^{\circ }$
are completely prime is shown in [Reference SigurdssonSig84] (see also [Reference JordanJor14, Remark 3.7]) and the rest of
![]() $(1)$
follows immediately for
$(1)$
follows immediately for
![]() $P$
.
$P$
.
Now suppose that
![]() $X_{0}\in P$
. If
$X_{0}\in P$
. If
![]() $P\in \operatorname{Spec}R$
or
$P\in \operatorname{Spec}R$
or
![]() $P\in \operatorname{PSpec}A$
then
$P\in \operatorname{PSpec}A$
then
![]() $X_{0}\ast R=X_{0}A\subseteq P$
, and
$X_{0}\ast R=X_{0}A\subseteq P$
, and
![]() $(1)$
follows by induction, considering the image of
$(1)$
follows by induction, considering the image of
![]() $P$
in
$P$
in
![]() $\operatorname{PSpec}A/\langle X_{0}\rangle =\operatorname{Spec}R/\langle X_{0}\rangle$
.
$\operatorname{PSpec}A/\langle X_{0}\rangle =\operatorname{Spec}R/\langle X_{0}\rangle$
.
For
![]() $(2)$
the case
$(2)$
the case
![]() $X_{0}\not \in P$
follows from [Reference JordanJor14, Corollary 4.4], applied to
$X_{0}\not \in P$
follows from [Reference JordanJor14, Corollary 4.4], applied to
![]() $P^{\circ }\subseteq R^{\circ }=A^{\circ }$
, and the case
$P^{\circ }\subseteq R^{\circ }=A^{\circ }$
, and the case
![]() $X_{0}\in P$
follows by induction, as above.◻
$X_{0}\in P$
follows by induction, as above.◻
We turn now to describing the topological space
![]() $\operatorname{Spec}R=\operatorname{PSpec}A$
. We note that this space has a natural stratification: for
$\operatorname{Spec}R=\operatorname{PSpec}A$
. We note that this space has a natural stratification: for
![]() $0\leqslant j\leqslant n+1$
, let
$0\leqslant j\leqslant n+1$
, let
It is immediate that
![]() $\operatorname{Spec}R$
is the disjoint union of the
$\operatorname{Spec}R$
is the disjoint union of the
![]() $\operatorname{Spec}_{i}(R)$
. By Proposition 3.7, we have
$\operatorname{Spec}_{i}(R)$
. By Proposition 3.7, we have
![]() $\operatorname{Spec}_{j}R\cong \operatorname{Spec}_{j-1}R(n-1,a+1)$
. Thus to describe the primes of
$\operatorname{Spec}_{j}R\cong \operatorname{Spec}_{j-1}R(n-1,a+1)$
. Thus to describe the primes of
![]() $R$
explicitly, it suffices by induction to describe the open stratum
$R$
explicitly, it suffices by induction to describe the open stratum
![]() $\operatorname{Spec}_{0}R$
. We have
$\operatorname{Spec}_{0}R$
. We have
![]() $\operatorname{Spec}_{0}(R)\cong \operatorname{Spec}R^{\circ }=\operatorname{PSpec}A^{\circ }$
, using (the proof of) Theorem 7.1.
$\operatorname{Spec}_{0}(R)\cong \operatorname{Spec}R^{\circ }=\operatorname{PSpec}A^{\circ }$
, using (the proof of) Theorem 7.1.
Before describing
![]() $\operatorname{PSpec}A^{\circ }=\operatorname{Spec}R^{\circ }$
, we establish some notation. Let
$\operatorname{PSpec}A^{\circ }=\operatorname{Spec}R^{\circ }$
, we establish some notation. Let
![]() $K$
be a commutative ring. By
$K$
be a commutative ring. By
![]() $\mathbb{P}_{K}(2,\ldots ,n)$
we denote the weighted projective space
$\mathbb{P}_{K}(2,\ldots ,n)$
we denote the weighted projective space
![]() $\mathbb{P}(2,\ldots ,n)$
with base
$\mathbb{P}(2,\ldots ,n)$
with base
![]() $\operatorname{Spec}K$
: explicitly,
$\operatorname{Spec}K$
: explicitly,
![]() $\mathbb{P}_{K}(2,\ldots ,n)=\operatorname{Proj}K[Y_{2},\ldots ,Y_{n}]$
(see [Reference HartshorneHar77, page 76]), where
$\mathbb{P}_{K}(2,\ldots ,n)=\operatorname{Proj}K[Y_{2},\ldots ,Y_{n}]$
(see [Reference HartshorneHar77, page 76]), where
![]() $K$
is assumed to be concentrated in degree
$K$
is assumed to be concentrated in degree
![]() $0$
, and
$0$
, and
![]() $\deg Y_{i}=i$
.
$\deg Y_{i}=i$
.
If
![]() $C$
is a graded ring, let
$C$
is a graded ring, let
![]() $\operatorname{Spec}_{\operatorname{gr}}(C)$
be the set of prime graded ideals of
$\operatorname{Spec}_{\operatorname{gr}}(C)$
be the set of prime graded ideals of
![]() $C$
, under the Zariski topology; if
$C$
, under the Zariski topology; if
![]() $C$
has multiple gradings, say
$C$
has multiple gradings, say
![]() $d$
and
$d$
and
![]() $e$
, we write
$e$
, we write
![]() $\operatorname{Spec}_{d-\operatorname{gr}}(C)$
or
$\operatorname{Spec}_{d-\operatorname{gr}}(C)$
or
![]() $\operatorname{Spec}_{e-\operatorname{gr}}(C)$
to indicate which grading is being used. Likewise, let
$\operatorname{Spec}_{e-\operatorname{gr}}(C)$
to indicate which grading is being used. Likewise, let
![]() $\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })=\{d\text{-graded Poisson primes of }A^{\circ }\}$
.
$\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })=\{d\text{-graded Poisson primes of }A^{\circ }\}$
.
For
![]() $n\geqslant 2$
let
$n\geqslant 2$
let
![]() $C(n)=\Bbbk [Z_{2},\ldots ,Z_{n}]$
, graded with
$C(n)=\Bbbk [Z_{2},\ldots ,Z_{n}]$
, graded with
![]() $\deg Z_{i}=i$
. Let
$\deg Z_{i}=i$
. Let
![]() $X(n)=\operatorname{Spec}_{\operatorname{gr}}C(n)$
. Note that
$X(n)=\operatorname{Spec}_{\operatorname{gr}}C(n)$
. Note that
![]() $X(n)=\mathbb{P}_{\Bbbk }(2,\ldots ,n)\sqcup \{C(n)_{+}=\langle Z_{2},\ldots ,Z_{n}\rangle \}$
and is
$X(n)=\mathbb{P}_{\Bbbk }(2,\ldots ,n)\sqcup \{C(n)_{+}=\langle Z_{2},\ldots ,Z_{n}\rangle \}$
and is
![]() $(n-2)$
-dimensional.
$(n-2)$
-dimensional.
The structure of
![]() $\operatorname{PSpec}A^{\circ }=\operatorname{Spec}R^{\circ }$
depends sensitively on the value of
$\operatorname{PSpec}A^{\circ }=\operatorname{Spec}R^{\circ }$
depends sensitively on the value of
![]() $a$
, as shown in the next result.
$a$
, as shown in the next result.
Theorem 7.5. Assume that
![]() $n\geqslant 2$
.
$n\geqslant 2$
.
(1) If
 $a\not \in \mathbb{Q}$
, then
$a\not \in \mathbb{Q}$
, then
 $\operatorname{PSpec}A^{\circ }$
is homeomorphic to
$\operatorname{PSpec}A^{\circ }$
is homeomorphic to
 $X(n)$
. Further, all primes of
$X(n)$
. Further, all primes of
 $R^{\circ }$
and Poisson primes of
$R^{\circ }$
and Poisson primes of
 $A^{\circ }$
are
$A^{\circ }$
are
 $d$
-graded.
$d$
-graded.(2) If
 $a\in \mathbb{Q}^{\times }$
, then
$a\in \mathbb{Q}^{\times }$
, then
 $\operatorname{PSpec}A^{\circ }$
is homeomorphic to the rational affine variety
$\operatorname{PSpec}A^{\circ }$
is homeomorphic to the rational affine variety
 $\operatorname{Spec}Z$
, where
$\operatorname{Spec}Z$
, where
 $Z$
is the Poisson center of
$Z$
is the Poisson center of
 $A^{\circ }$
, and has dimension
$A^{\circ }$
, and has dimension
 $(n-1)$
. Further,
$(n-1)$
. Further,
 $\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
is homeomorphic to
$\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
is homeomorphic to
 $X(n)$
.
$X(n)$
.(3) If
 $a=0$
, then
$a=0$
, then
 $\operatorname{PSpec}A^{\circ }$
is the disjoint union of a stratum homeomorphic to
$\operatorname{PSpec}A^{\circ }$
is the disjoint union of a stratum homeomorphic to
 $\mathbb{P}_{\Bbbk [X_{0}^{\pm 1}]}(2,\ldots ,n)$
and
$\mathbb{P}_{\Bbbk [X_{0}^{\pm 1}]}(2,\ldots ,n)$
and
 $\operatorname{PSpec}A^{\circ }/(Y_{2},\ldots ,Y_{n})\cong \mathbb{A}^{2}\smallsetminus V(X_{0})$
and has dimension
$\operatorname{PSpec}A^{\circ }/(Y_{2},\ldots ,Y_{n})\cong \mathbb{A}^{2}\smallsetminus V(X_{0})$
and has dimension
 $\max \{n-1,2\}$
. We have that
$\max \{n-1,2\}$
. We have that
 $\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
is the disjoint union of a stratum homeomorphic to
$\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
is the disjoint union of a stratum homeomorphic to
 $\mathbb{P}(2,\ldots ,n)$
and a stratum homeomorphic to
$\mathbb{P}(2,\ldots ,n)$
and a stratum homeomorphic to
 $\mathbb{A}^{1}$
.
$\mathbb{A}^{1}$
.(4) Further, as long as
 $a\neq 0$
, then
$a\neq 0$
, then
 $\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
does not depend on
$\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
does not depend on
 $a$
: that is, an ideal
$a$
: that is, an ideal
 $P$
of
$P$
of
 $\Bbbk [X_{0},\ldots ,X_{n}]$
is a Poisson prime of some
$\Bbbk [X_{0},\ldots ,X_{n}]$
is a Poisson prime of some
 $A(n,a)^{\circ }$
(with
$A(n,a)^{\circ }$
(with
 $a\neq 0$
) if and only if
$a\neq 0$
) if and only if
 $P$
is a Poisson prime of all
$P$
is a Poisson prime of all
 $A(n,a)^{\circ }$
.
$A(n,a)^{\circ }$
.
We immediately obtain:
Corollary 7.6. Let
![]() $n\geqslant 1$
and let
$n\geqslant 1$
and let
![]() $a\in \Bbbk$
. Then
$a\in \Bbbk$
. Then
![]() $\operatorname{Spec}R(n,a)\cong \operatorname{PSpec}A(n,a)$
is a union of quasiprojective rational varieties and has dimension:
$\operatorname{Spec}R(n,a)\cong \operatorname{PSpec}A(n,a)$
is a union of quasiprojective rational varieties and has dimension:
∙
 $\max \{n-2,1\}$
if
$\max \{n-2,1\}$
if
 $a\not \in \mathbb{Q}$
;
$a\not \in \mathbb{Q}$
;∙
 $\max \{n-1,1\}$
if
$\max \{n-1,1\}$
if
 $a\in \mathbb{Q}$
and
$a\in \mathbb{Q}$
and
 $(n,a)\not \in \{(2,-1),(1,0)\}$
;
$(n,a)\not \in \{(2,-1),(1,0)\}$
;∙
 $2$
if
$2$
if
 $(n,a)\in \{(2,-1),(1,0)\}$
.
$(n,a)\in \{(2,-1),(1,0)\}$
.
Example 7.7. In the case
![]() $a\in \mathbb{Q}^{\times }$
, it is not necessarily true that Poisson primes of
$a\in \mathbb{Q}^{\times }$
, it is not necessarily true that Poisson primes of
![]() $A^{\circ }$
are centrally generated. For example, let
$A^{\circ }$
are centrally generated. For example, let
![]() $n=2$
and
$n=2$
and
![]() $a=-7/4$
. Recall that
$a=-7/4$
. Recall that
![]() $Y_{2}=X_{2}-(X_{1}^{2}/2X_{0})$
. Then
$Y_{2}=X_{2}-(X_{1}^{2}/2X_{0})$
. Then
![]() $\unicode[STIX]{x1D6E5}(Y_{2})=0$
and
$\unicode[STIX]{x1D6E5}(Y_{2})=0$
and
![]() $\unicode[STIX]{x1D6E4}(Y_{2})=(1/4)Y_{2}$
. By Proposition 3.21,
$\unicode[STIX]{x1D6E4}(Y_{2})=(1/4)Y_{2}$
. By Proposition 3.21,
![]() $Y_{2}$
is Poisson normal in
$Y_{2}$
is Poisson normal in
![]() $A^{\circ }$
.
$A^{\circ }$
.
We see that the Poisson center of
![]() $A^{\circ }$
is
$A^{\circ }$
is
![]() $Z=\Bbbk [X_{0}Y_{2}^{7}]$
, so the Poisson ideal
$Z=\Bbbk [X_{0}Y_{2}^{7}]$
, so the Poisson ideal
![]() $\langle Y_{2}\rangle$
of
$\langle Y_{2}\rangle$
of
![]() $A^{\circ }$
is not centrally generated. However,
$A^{\circ }$
is not centrally generated. However,
![]() $Y_{2}$
is the unique Poisson prime of
$Y_{2}$
is the unique Poisson prime of
![]() $A^{\circ }$
with
$A^{\circ }$
with
![]() $\langle Y_{2}\rangle \cap Z=\langle X_{0}Y_{2}^{7}\rangle$
.
$\langle Y_{2}\rangle \cap Z=\langle X_{0}Y_{2}^{7}\rangle$
.
The situation in the example is typical. Theorem 7.5(2) will follow from:
Proposition 7.8. Assume that
![]() $a\in \mathbb{Q}^{\times }$
. The map
$a\in \mathbb{Q}^{\times }$
. The map
is a homeomorphism. The inverse map is defined by
Further,
![]() $\operatorname{Spec}Z$
is a rational variety of dimension
$\operatorname{Spec}Z$
is a rational variety of dimension
![]() $n-1$
.
$n-1$
.
As an immediate consequence, we have:
Corollary 7.9. If
![]() $a\in \mathbb{Q}^{\times }$
, the map
$a\in \mathbb{Q}^{\times }$
, the map
![]() $P\mapsto P[X_{0}^{-1}]\cap Z$
induces a homeomorphism between
$P\mapsto P[X_{0}^{-1}]\cap Z$
induces a homeomorphism between
![]() $\operatorname{PSpec}(A)\smallsetminus V(X_{0})\cong \operatorname{PSpec}(A^{\circ })$
and
$\operatorname{PSpec}(A)\smallsetminus V(X_{0})\cong \operatorname{PSpec}(A^{\circ })$
and
![]() $\operatorname{Spec}(Z)$
.◻
$\operatorname{Spec}(Z)$
.◻
Proposition 7.8 will follow from a general lemma on gradings of localized polynomial rings.
Lemma 7.10. Let
![]() $B=\Bbbk [X_{0}^{\pm 1},X_{1},\ldots ,X_{m}]$
, where
$B=\Bbbk [X_{0}^{\pm 1},X_{1},\ldots ,X_{m}]$
, where
![]() $\deg X_{i}=a_{i}\in \mathbb{Z}$
. Assume that
$\deg X_{i}=a_{i}\in \mathbb{Z}$
. Assume that
![]() $a_{0}\neq 0$
. Write the
$a_{0}\neq 0$
. Write the
![]() $\mathbb{Z}$
-grading on
$\mathbb{Z}$
-grading on
![]() $B$
as
$B$
as
![]() $B=\bigoplus _{n\in \mathbb{Z}}B_{n}$
, and let
$B=\bigoplus _{n\in \mathbb{Z}}B_{n}$
, and let
![]() $Z=B_{0}$
.
$Z=B_{0}$
.
Let
![]() $Q_{0}\in \operatorname{Spec}Z$
and let
$Q_{0}\in \operatorname{Spec}Z$
and let
![]() $N=\sqrt{Q_{0}B}$
. Then:
$N=\sqrt{Q_{0}B}$
. Then:
(1)
 $N$
is prime;
$N$
is prime;(2)
 $\operatorname{Kdim}(B/N)=1+\operatorname{Kdim}(Z/Q_{0})$
.
$\operatorname{Kdim}(B/N)=1+\operatorname{Kdim}(Z/Q_{0})$
.(3) The map
 $Q_{0}\mapsto \sqrt{Q_{0}B}$
gives a homeomorphism
$Q_{0}\mapsto \sqrt{Q_{0}B}$
gives a homeomorphism
 $\unicode[STIX]{x1D702}:\operatorname{Spec}Z\rightarrow \operatorname{Spec}_{\operatorname{gr}}(B)$
. The inverse map is given by
$\unicode[STIX]{x1D702}:\operatorname{Spec}Z\rightarrow \operatorname{Spec}_{\operatorname{gr}}(B)$
. The inverse map is given by
 $Q\mapsto Q\cap Z$
. Further,
$Q\mapsto Q\cap Z$
. Further,
 $\operatorname{Spec}Z$
is a rational variety of dimension
$\operatorname{Spec}Z$
is a rational variety of dimension
 $n-1$
: that is, the fraction field
$n-1$
: that is, the fraction field
 $\operatorname{Frac}(Z)$
of
$\operatorname{Frac}(Z)$
of
 $Z$
is isomorphic to
$Z$
is isomorphic to
 $\Bbbk (t_{0},\ldots ,t_{n-2})$
.
$\Bbbk (t_{0},\ldots ,t_{n-2})$
.
Proof.
![]() $(1)$
Let
$(1)$
Let
![]() $B^{\prime }=\bigoplus _{k\in \mathbb{Z}}B_{ka_{0}}\cong Z[X_{0}^{\pm 1}]$
. Suppose that
$B^{\prime }=\bigoplus _{k\in \mathbb{Z}}B_{ka_{0}}\cong Z[X_{0}^{\pm 1}]$
. Suppose that
![]() $N$
is not prime; then there are
$N$
is not prime; then there are
![]() $x,y\not \in N$
with
$x,y\not \in N$
with
![]() $xy\in N$
, so
$xy\in N$
, so
![]() $(xy)^{m}\in Q_{0}B$
and
$(xy)^{m}\in Q_{0}B$
and
![]() $(xy)^{mp}\in Q_{0}B^{\prime }$
for some
$(xy)^{mp}\in Q_{0}B^{\prime }$
for some
![]() $m,p\in \mathbb{Z}_{{\geqslant}1}$
. Thus either
$m,p\in \mathbb{Z}_{{\geqslant}1}$
. Thus either
![]() $x^{mp}$
or
$x^{mp}$
or
![]() $y^{mp}$
is in
$y^{mp}$
is in
![]() $Q_{0}B$
, since
$Q_{0}B$
, since
![]() $Q_{0}B^{\prime }\subseteq Q_{0}B$
is a prime ideal of
$Q_{0}B^{\prime }\subseteq Q_{0}B$
is a prime ideal of
![]() $B^{\prime }$
. This is a contradiction.
$B^{\prime }$
. This is a contradiction.
![]() $(2)$
Since
$(2)$
Since
![]() $B$
is module-finite over
$B$
is module-finite over
![]() $B^{\prime }$
, therefore
$B^{\prime }$
, therefore
![]() $B/Q_{0}B$
is module-finite over
$B/Q_{0}B$
is module-finite over
![]() $B^{\prime }/Q_{0}B^{\prime }\cong (Z/Q_{0})[X_{0}^{\pm 1}]$
. Thus
$B^{\prime }/Q_{0}B^{\prime }\cong (Z/Q_{0})[X_{0}^{\pm 1}]$
. Thus
![]() $\operatorname{Kdim}B/N=\operatorname{Kdim}B/Q_{0}B=\operatorname{Kdim}B^{\prime }/Q_{0}B^{\prime }=1+\operatorname{Kdim}Z/Q_{0}$
.
$\operatorname{Kdim}B/N=\operatorname{Kdim}B/Q_{0}B=\operatorname{Kdim}B^{\prime }/Q_{0}B^{\prime }=1+\operatorname{Kdim}Z/Q_{0}$
.
![]() $(3)$
Let
$(3)$
Let
![]() ${\mathcal{C}}=Z\smallsetminus Q_{0}$
and let
${\mathcal{C}}=Z\smallsetminus Q_{0}$
and let
![]() $T=B{\mathcal{C}}^{-1}/N{\mathcal{C}}^{-1}$
. Since
$T=B{\mathcal{C}}^{-1}/N{\mathcal{C}}^{-1}$
. Since
![]() $N$
is graded and prime,
$N$
is graded and prime,
![]() $T$
is a graded domain. Let
$T$
is a graded domain. Let
![]() $d=\min \{k\in \mathbb{Z}_{{\geqslant}0}\mid T_{k}\neq 0\}$
and let
$d=\min \{k\in \mathbb{Z}_{{\geqslant}0}\mid T_{k}\neq 0\}$
and let
![]() $0\neq x\in T_{d}$
.
$0\neq x\in T_{d}$
.
We claim that
![]() $T\cong \operatorname{Frac}(Z/Q_{0})[x^{\pm 1}]$
. Certainly
$T\cong \operatorname{Frac}(Z/Q_{0})[x^{\pm 1}]$
. Certainly
![]() $T_{0}=Z{\mathcal{C}}^{-1}/Q_{0}{\mathcal{C}}^{-1}\cong \operatorname{Frac}(Z/Q_{0})$
. Now,
$T_{0}=Z{\mathcal{C}}^{-1}/Q_{0}{\mathcal{C}}^{-1}\cong \operatorname{Frac}(Z/Q_{0})$
. Now,
![]() $X_{0}$
and
$X_{0}$
and
![]() $X_{0}^{-1}$
map to nonzero elements of
$X_{0}^{-1}$
map to nonzero elements of
![]() $T$
under the natural map
$T$
under the natural map
![]() $B\rightarrow T$
. By abuse of notation, let
$B\rightarrow T$
. By abuse of notation, let
![]() $X_{0}$
also denote the image of
$X_{0}$
also denote the image of
![]() $X_{0}$
in
$X_{0}$
in
![]() $T$
. A straightforward combinatorial argument shows that
$T$
. A straightforward combinatorial argument shows that
![]() $T=\bigoplus _{k\in \mathbb{Z}}T_{kd}$
. In particular,
$T=\bigoplus _{k\in \mathbb{Z}}T_{kd}$
. In particular,
![]() $a_{0}=d\ell$
for some
$a_{0}=d\ell$
for some
![]() $\ell$
and so
$\ell$
and so
![]() $x^{\ell }(X_{0})^{-1}\in T_{0}$
is invertible. Thus
$x^{\ell }(X_{0})^{-1}\in T_{0}$
is invertible. Thus
![]() $x$
is invertible in
$x$
is invertible in
![]() $T$
. It follows that
$T$
. It follows that
![]() $T_{dk}=T_{0}x^{k}$
for all
$T_{dk}=T_{0}x^{k}$
for all
![]() $k$
, completing the proof of the claim.
$k$
, completing the proof of the claim.
Since
![]() $T\cong \operatorname{Frac}(Z/Q_{0})[x^{\pm 1}]$
is a Laurent polynomial ring over a field, it has no nontrivial graded ideals. Now,
$T\cong \operatorname{Frac}(Z/Q_{0})[x^{\pm 1}]$
is a Laurent polynomial ring over a field, it has no nontrivial graded ideals. Now,
![]() $\operatorname{Spec}_{\operatorname{gr}}T$
is in bijection with
$\operatorname{Spec}_{\operatorname{gr}}T$
is in bijection with
where we have used part
![]() $(1)$
of the lemma. Thus there is only one such
$(1)$
of the lemma. Thus there is only one such
![]() $Q$
, namely
$Q$
, namely
![]() $N$
.
$N$
.
Define
![]() $\unicode[STIX]{x1D703}:\operatorname{Spec}_{\operatorname{gr}}B\rightarrow \operatorname{Spec}Z$
by
$\unicode[STIX]{x1D703}:\operatorname{Spec}_{\operatorname{gr}}B\rightarrow \operatorname{Spec}Z$
by
![]() $\unicode[STIX]{x1D703}(Q)=Q\cap Z$
. The argument above shows that if
$\unicode[STIX]{x1D703}(Q)=Q\cap Z$
. The argument above shows that if
![]() $Q\in \operatorname{Spec}_{\operatorname{gr}}B$
, then
$Q\in \operatorname{Spec}_{\operatorname{gr}}B$
, then
![]() $Q=\unicode[STIX]{x1D702}\unicode[STIX]{x1D703}(Q)$
. Since
$Q=\unicode[STIX]{x1D702}\unicode[STIX]{x1D703}(Q)$
. Since
![]() $\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}$
is easily seen to be the identity on
$\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}$
is easily seen to be the identity on
![]() $\operatorname{Spec}Z$
, therefore
$\operatorname{Spec}Z$
, therefore
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D702}^{-1}$
. As
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D702}^{-1}$
. As
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $\unicode[STIX]{x1D703}$
clearly preserve inclusions, they are continuous and thus homeomorphisms.
$\unicode[STIX]{x1D703}$
clearly preserve inclusions, they are continuous and thus homeomorphisms.
Since
![]() $Z$
is a normal semigroup algebra,
$Z$
is a normal semigroup algebra,
![]() $\operatorname{Spec}Z$
is rational.◻
$\operatorname{Spec}Z$
is rational.◻
We next give an explicit characterization of Poisson primitive ideals of
![]() $A^{\circ }$
if
$A^{\circ }$
if
![]() $a\in \mathbb{Q}$
. By Theorem 7.1 these are the same as the primitive ideals of
$a\in \mathbb{Q}$
. By Theorem 7.1 these are the same as the primitive ideals of
![]() $R^{\circ }$
. Recall from the end of Section 3 that we define a grading
$R^{\circ }$
. Recall from the end of Section 3 that we define a grading
![]() $A^{\circ }=\bigoplus _{e\in \Bbbk }A^{\circ }(e)$
by setting
$A^{\circ }=\bigoplus _{e\in \Bbbk }A^{\circ }(e)$
by setting
![]() $A^{\circ }(e)$
to be the
$A^{\circ }(e)$
to be the
![]() $e$
-eigenspace of
$e$
-eigenspace of
![]() $\unicode[STIX]{x1D6E4}_{a}$
. Moreover, notice that
$\unicode[STIX]{x1D6E4}_{a}$
. Moreover, notice that
![]() $(A^{\circ })^{\unicode[STIX]{x1D6E5}}$
is an
$(A^{\circ })^{\unicode[STIX]{x1D6E5}}$
is an
![]() $e$
-graded subalgebra of
$e$
-graded subalgebra of
![]() $A^{\circ }$
.
$A^{\circ }$
.
Corollary 7.11. If
![]() $a\in \mathbb{Q}^{\times }$
then
$a\in \mathbb{Q}^{\times }$
then
![]() $\operatorname{PSpec}A^{\circ }$
is homeomorphic to
$\operatorname{PSpec}A^{\circ }$
is homeomorphic to
![]() $\operatorname{Spec}Z$
. Furthermore, a Poisson prime
$\operatorname{Spec}Z$
. Furthermore, a Poisson prime
![]() $P$
of
$P$
of
![]() $\operatorname{PSpec}A^{\circ }$
is Poisson primitive if and only if
$\operatorname{PSpec}A^{\circ }$
is Poisson primitive if and only if
![]() $P\cap Z$
is a maximal ideal of
$P\cap Z$
is a maximal ideal of
![]() $Z$
.
$Z$
.
Proof. Let
![]() $B=\Bbbk [X_{0}^{\pm 1},Y_{2},\ldots ,Y_{n}]=(A^{\circ })^{\unicode[STIX]{x1D6E5}}$
. Let
$B=\Bbbk [X_{0}^{\pm 1},Y_{2},\ldots ,Y_{n}]=(A^{\circ })^{\unicode[STIX]{x1D6E5}}$
. Let
![]() $Z$
be the Poisson center of
$Z$
be the Poisson center of
![]() $A^{\circ }$
. By Proposition 3.21,
$A^{\circ }$
. By Proposition 3.21,
![]() $Z=B^{\unicode[STIX]{x1D6E4}_{a}}=B(0)$
. Since
$Z=B^{\unicode[STIX]{x1D6E4}_{a}}=B(0)$
. Since
![]() $a\neq 0$
,
$a\neq 0$
,
![]() $X_{0}\in \unicode[STIX]{x1D6FF}(B)$
so no nontrivial ideal of
$X_{0}\in \unicode[STIX]{x1D6FF}(B)$
so no nontrivial ideal of
![]() $A^{\circ }$
can contain
$A^{\circ }$
can contain
![]() $\unicode[STIX]{x1D6FF}(B)$
. By Proposition 7.2, there is an inclusion-preserving bijection
$\unicode[STIX]{x1D6FF}(B)$
. By Proposition 7.2, there is an inclusion-preserving bijection
![]() $\unicode[STIX]{x1D70C}$
between
$\unicode[STIX]{x1D70C}$
between
![]() $\operatorname{PSpec}A^{\circ }$
and the set of
$\operatorname{PSpec}A^{\circ }$
and the set of
![]() $\unicode[STIX]{x1D6FF}$
-prime ideals of
$\unicode[STIX]{x1D6FF}$
-prime ideals of
![]() $B$
, defined by
$B$
, defined by
![]() $\unicode[STIX]{x1D70C}(P)=P\cap B$
. Note that a
$\unicode[STIX]{x1D70C}(P)=P\cap B$
. Note that a
![]() $\unicode[STIX]{x1D6FF}$
-prime of
$\unicode[STIX]{x1D6FF}$
-prime of
![]() $B$
is the same as an
$B$
is the same as an
![]() $e$
-graded prime of
$e$
-graded prime of
![]() $B$
. Thus by Lemma 7.10 the map
$B$
. Thus by Lemma 7.10 the map
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D703}\unicode[STIX]{x1D70C}:\operatorname{Spec}A^{\circ }\rightarrow \operatorname{Spec}Z$
is a homeomorphism. The inverse to
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D703}\unicode[STIX]{x1D70C}:\operatorname{Spec}A^{\circ }\rightarrow \operatorname{Spec}Z$
is a homeomorphism. The inverse to
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
By [Reference JordanJor14, Corollary 4.4],
![]() $P\in \operatorname{PSpec}A^{\circ }$
is Poisson primitive if and only if
$P\in \operatorname{PSpec}A^{\circ }$
is Poisson primitive if and only if
![]() $P\cap B$
is a
$P\cap B$
is a
![]() $\unicode[STIX]{x1D6FF}$
-primitive ideal of
$\unicode[STIX]{x1D6FF}$
-primitive ideal of
![]() $B$
, that is,
$B$
, that is,
![]() $P\cap B$
is the largest
$P\cap B$
is the largest
![]() $\unicode[STIX]{x1D6FF}$
-stable ideal of
$\unicode[STIX]{x1D6FF}$
-stable ideal of
![]() $B$
contained in some maximal ideal
$B$
contained in some maximal ideal
![]() $M$
. Since an ideal of
$M$
. Since an ideal of
![]() $B$
is
$B$
is
![]() $\unicode[STIX]{x1D6FF}$
-stable
$\unicode[STIX]{x1D6FF}$
-stable
![]() $\;\Longleftrightarrow \;$
it is
$\;\Longleftrightarrow \;$
it is
![]() $\unicode[STIX]{x1D6E4}_{a}$
-stable, a
$\unicode[STIX]{x1D6E4}_{a}$
-stable, a
![]() $\unicode[STIX]{x1D6FF}$
-primitive ideal of
$\unicode[STIX]{x1D6FF}$
-primitive ideal of
![]() $B$
is a maximal
$B$
is a maximal
![]() $e$
-graded ideal of
$e$
-graded ideal of
![]() $B$
, and by Lemma 7.10 these are precisely ideals of the form
$B$
, and by Lemma 7.10 these are precisely ideals of the form
![]() $\unicode[STIX]{x1D713}(M_{0})$
for
$\unicode[STIX]{x1D713}(M_{0})$
for
![]() $M_{0}=P\cap B\cap Z=P\cap Z\in \operatorname{maxspec}Z$
.◻
$M_{0}=P\cap B\cap Z=P\cap Z\in \operatorname{maxspec}Z$
.◻
We next assume that
![]() $a\neq 0$
, and consider
$a\neq 0$
, and consider
![]() $d$
-graded Poisson primes of
$d$
-graded Poisson primes of
![]() $A^{\circ }$
, which by Theorem 7.1 may be identified with
$A^{\circ }$
, which by Theorem 7.1 may be identified with
![]() $d$
-graded primes of
$d$
-graded primes of
![]() $R^{\circ }$
. For
$R^{\circ }$
. For
![]() $2\leqslant i\leqslant n$
, let
$2\leqslant i\leqslant n$
, let
![]() $Z_{i}=Y_{i}X_{0}^{-1}$
and
$Z_{i}=Y_{i}X_{0}^{-1}$
and
![]() $C=\Bbbk [Z_{2},\ldots ,Z_{n}]$
. The
$C=\Bbbk [Z_{2},\ldots ,Z_{n}]$
. The
![]() $e$
-grading on
$e$
-grading on
![]() $A^{\circ }$
restricts to
$A^{\circ }$
restricts to
![]() $C$
, with
$C$
, with
![]() $e(Z_{i})=i$
.
$e(Z_{i})=i$
.
Proposition 7.12. If
![]() $a\neq 0$
, then
$a\neq 0$
, then
![]() $\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
is homeomorphic to
$\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
is homeomorphic to
![]() $\operatorname{Spec}_{e-\operatorname{gr}}(C)\cong X(n)$
. Further, as long as
$\operatorname{Spec}_{e-\operatorname{gr}}(C)\cong X(n)$
. Further, as long as
![]() $a\neq 0$
, then
$a\neq 0$
, then
![]() $\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
does not depend on
$\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
does not depend on
![]() $a$
in the sense of Theorem 7.5(4).
$a$
in the sense of Theorem 7.5(4).
Proof. Note that
![]() $C$
is precisely
$C$
is precisely
![]() $B_{0}=\{\!b\in B\mid b\text{ is }d\text{-homogeneous}\text{of degree }0\!\}$
. As in the proof of Corollary 7.11, there is an inclusion-preserving bijection between
$B_{0}=\{\!b\in B\mid b\text{ is }d\text{-homogeneous}\text{of degree }0\!\}$
. As in the proof of Corollary 7.11, there is an inclusion-preserving bijection between
![]() $\operatorname{PSpec}(A^{\circ })$
and
$\operatorname{PSpec}(A^{\circ })$
and
![]() $\operatorname{Spec}_{e-\operatorname{gr}}(B)$
, and it is clear that this bijection takes
$\operatorname{Spec}_{e-\operatorname{gr}}(B)$
, and it is clear that this bijection takes
![]() $d$
-graded primes to
$d$
-graded primes to
![]() $d$
-graded primes: in other words,
$d$
-graded primes: in other words,
![]() $\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
is homeomorphic to the set of
$\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
is homeomorphic to the set of
![]() $(d,e)$
-bigraded primes of
$(d,e)$
-bigraded primes of
![]() $B$
, via the map
$B$
, via the map
![]() $P\mapsto P\cap B$
. Since
$P\mapsto P\cap B$
. Since
![]() $B=C[X_{0}^{\pm 1}]$
is strongly
$B=C[X_{0}^{\pm 1}]$
is strongly
![]() $d$
-graded, we have
$d$
-graded, we have
![]() $\operatorname{Spec}_{d-\operatorname{gr}}(B)\cong \operatorname{Spec}C$
. Thus
$\operatorname{Spec}_{d-\operatorname{gr}}(B)\cong \operatorname{Spec}C$
. Thus
![]() $\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
is homeomorphic to
$\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })$
is homeomorphic to
![]() $\operatorname{Spec}_{e-\operatorname{gr}}(C)$
via
$\operatorname{Spec}_{e-\operatorname{gr}}(C)$
via
![]() $P\mapsto P\cap C$
. But
$P\mapsto P\cap C$
. But
![]() $\operatorname{Spec}_{e-\operatorname{gr}}(C)$
is homeomorphic by definition to
$\operatorname{Spec}_{e-\operatorname{gr}}(C)$
is homeomorphic by definition to
![]() $X(n)$
.
$X(n)$
.
For the final statement, note that the definition of
![]() $C$
, the
$C$
, the
![]() $e$
-grading on
$e$
-grading on
![]() $C$
, and the restriction homeomorphism
$C$
, and the restriction homeomorphism
![]() $\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })\rightarrow \operatorname{Spec}_{e-\operatorname{gr}}(C)$
do not depend on the value of
$\operatorname{PSpec}_{d-\operatorname{gr}}(A^{\circ })\rightarrow \operatorname{Spec}_{e-\operatorname{gr}}(C)$
do not depend on the value of
![]() $a$
.◻
$a$
.◻
The result above is particularly strong if
![]() $a\not \in \mathbb{Q}$
, since we then have:
$a\not \in \mathbb{Q}$
, since we then have:
Proposition 7.13. If
![]() $a\not \in \mathbb{Q}$
, then all Poisson primes of
$a\not \in \mathbb{Q}$
, then all Poisson primes of
![]() $A^{\circ }$
are
$A^{\circ }$
are
![]() $d$
-graded.
$d$
-graded.
Proof. We have seen that
![]() $\operatorname{PSpec}(A^{\circ })\cong \operatorname{Spec}_{e-\operatorname{gr}}(B)$
, where
$\operatorname{PSpec}(A^{\circ })\cong \operatorname{Spec}_{e-\operatorname{gr}}(B)$
, where
![]() $B=\Bbbk [X_{0}^{\pm 1},Y_{2},\ldots ,Y_{n}]$
. Let
$B=\Bbbk [X_{0}^{\pm 1},Y_{2},\ldots ,Y_{n}]$
. Let
![]() $\mathbb{S}=\{e(b)~|~b\in B\}$
, which is clearly equal to
$\mathbb{S}=\{e(b)~|~b\in B\}$
, which is clearly equal to
![]() $\mathbb{Z}a+\mathbb{N}$
. Since
$\mathbb{Z}a+\mathbb{N}$
. Since
![]() $a\not \in \mathbb{Q}$
, we have
$a\not \in \mathbb{Q}$
, we have
![]() $\mathbb{S}\cong \mathbb{Z}\oplus \mathbb{N}$
as a semigroup, and it follows that if
$\mathbb{S}\cong \mathbb{Z}\oplus \mathbb{N}$
as a semigroup, and it follows that if
![]() $b\in B$
is
$b\in B$
is
![]() $e$
-homogeneous then
$e$
-homogeneous then
![]() $b$
is
$b$
is
![]() $d$
-homogeneous.◻
$d$
-homogeneous.◻
We now combine the previous results to prove Theorem 7.5.
Proof of Theorem 7.5.
![]() $(1)$
follows from Propositions 7.12 and 7.13, and
$(1)$
follows from Propositions 7.12 and 7.13, and
![]() $(2)$
is Corollary 7.11 and Proposition 7.12 again.
$(2)$
is Corollary 7.11 and Proposition 7.12 again.
For
![]() $(3)$
, let
$(3)$
, let
![]() $B_{+}=\sum BY_{i}$
; we have
$B_{+}=\sum BY_{i}$
; we have
![]() $B_{+}=\unicode[STIX]{x1D6FF}(B)B$
. Note that by Proposition 7.2,
$B_{+}=\unicode[STIX]{x1D6FF}(B)B$
. Note that by Proposition 7.2,
![]() $\operatorname{PSpec}A^{\circ }$
is equal to the disjoint union of:
$\operatorname{PSpec}A^{\circ }$
is equal to the disjoint union of:
and
As we have repeatedly seen above,
![]() $\unicode[STIX]{x1D6FF}$
-prime ideals of
$\unicode[STIX]{x1D6FF}$
-prime ideals of
![]() $B$
are the same as
$B$
are the same as
![]() $e$
-graded ideals: that is, (7.14) is homeomorphic to
$e$
-graded ideals: that is, (7.14) is homeomorphic to
On the other hand, (7.15) is clearly homeomorphic to the spectrum of
![]() $A^{\circ }/(Y_{2},\ldots ,Y_{n})\cong \Bbbk [X_{0}^{\pm 1},X_{1}]$
(with trivial Poisson bracket).
$A^{\circ }/(Y_{2},\ldots ,Y_{n})\cong \Bbbk [X_{0}^{\pm 1},X_{1}]$
(with trivial Poisson bracket).
Finally,
![]() $(4)$
follows from Proposition 7.12.◻
$(4)$
follows from Proposition 7.12.◻
Corollary 7.16. If
![]() $a\not \in \{-n+1,\ldots ,-1,0\}$
then
$a\not \in \{-n+1,\ldots ,-1,0\}$
then
![]() $\operatorname{PSpec}_{d-\operatorname{gr}}A(n,a)=\operatorname{Spec}_{d-\operatorname{gr}}R(n,a)$
does not depend on
$\operatorname{PSpec}_{d-\operatorname{gr}}A(n,a)=\operatorname{Spec}_{d-\operatorname{gr}}R(n,a)$
does not depend on
![]() $a$
. In particular
$a$
. In particular
![]() $\operatorname{Spec}R(n,a)\cong \operatorname{Spec}R(n,b)$
for any
$\operatorname{Spec}R(n,a)\cong \operatorname{Spec}R(n,b)$
for any
![]() $a,b\notin \mathbb{Q}$
.
$a,b\notin \mathbb{Q}$
.
8 Dixmier–Moeglin equivalences and skewfields
In this section we show that the algebra
![]() $R(n,a)$
satisfies the Dixmier–Moeglin equivalence (DME). Recall that primitive ideals are annihilators of simple modules. In particular they are not easily distinguished among the primes. The DME characterizes them with algebraic and topological properties. A prime ideal
$R(n,a)$
satisfies the Dixmier–Moeglin equivalence (DME). Recall that primitive ideals are annihilators of simple modules. In particular they are not easily distinguished among the primes. The DME characterizes them with algebraic and topological properties. A prime ideal
![]() $P$
in a Noetherian ring
$P$
in a Noetherian ring
![]() $R$
is said rational provided that the field
$R$
is said rational provided that the field
![]() $Z(\operatorname{Frac}R/P)$
is algebraic over the ground field, and is said locally closed if the point
$Z(\operatorname{Frac}R/P)$
is algebraic over the ground field, and is said locally closed if the point
![]() $\{P\}$
is locally closed in
$\{P\}$
is locally closed in
![]() $\operatorname{Spec}R$
(with respect to the Zariski topology). We say that the Dixmier–Moeglin equivalence holds for a given Noetherian algebra if the sets of primitive ideals, locally closed ideals and rational ideals coincide. This idea originated in the work of Dixmier and Moeglin who showed that for any finite-dimensional complex Lie algebras, theses sets are equal.
$\operatorname{Spec}R$
(with respect to the Zariski topology). We say that the Dixmier–Moeglin equivalence holds for a given Noetherian algebra if the sets of primitive ideals, locally closed ideals and rational ideals coincide. This idea originated in the work of Dixmier and Moeglin who showed that for any finite-dimensional complex Lie algebras, theses sets are equal.
Thanks to our result on the DME we prove a transfer result which says that the Poisson algebra
![]() $A(n,a)$
satisfies a similar equivalence, the so-called Poisson Dixmier–Moeglin equivalence (PDME), which we recall later. To prove our results on the DME we relate
$A(n,a)$
satisfies a similar equivalence, the so-called Poisson Dixmier–Moeglin equivalence (PDME), which we recall later. To prove our results on the DME we relate
![]() $R(n,a)$
to the enveloping algebra of a solvable Lie algebra sitting inside the localization
$R(n,a)$
to the enveloping algebra of a solvable Lie algebra sitting inside the localization
![]() $R(n,a)^{\circ }$
. With the Gelfand–Kirillov conjecture [Reference Gelfand and KirillovGK66, Section 5] in mind, this motivated us to investigate the skewfield of fractions of
$R(n,a)^{\circ }$
. With the Gelfand–Kirillov conjecture [Reference Gelfand and KirillovGK66, Section 5] in mind, this motivated us to investigate the skewfield of fractions of
![]() $R(n,a)$
at the end of this section.
$R(n,a)$
at the end of this section.
Let
![]() $R=R(n,a)$
and recall that
$R=R(n,a)$
and recall that
![]() $R^{\circ }=R[X_{0}^{-1}]$
. We denote by
$R^{\circ }=R[X_{0}^{-1}]$
. We denote by
![]() $T$
the subalgebra of
$T$
the subalgebra of
![]() $R^{\circ }$
generated by
$R^{\circ }$
generated by
![]() $X_{0},X_{1},Y_{2},\ldots ,Y_{n}$
. Setting
$X_{0},X_{1},Y_{2},\ldots ,Y_{n}$
. Setting
![]() $C:=\Bbbk [X_{0},Y_{2},\ldots ,Y_{n}]$
we have that
$C:=\Bbbk [X_{0},Y_{2},\ldots ,Y_{n}]$
we have that
![]() $T=C[X_{1};\unicode[STIX]{x1D6FF}]$
, where
$T=C[X_{1};\unicode[STIX]{x1D6FF}]$
, where
![]() $\unicode[STIX]{x1D6FF}=X_{0}\unicode[STIX]{x1D6E4}_{a}$
is a derivation of the commutative ring
$\unicode[STIX]{x1D6FF}=X_{0}\unicode[STIX]{x1D6E4}_{a}$
is a derivation of the commutative ring
![]() $C$
. Moreover, we set
$C$
. Moreover, we set
![]() $Y_{0}:=X_{0}$
and we denote by
$Y_{0}:=X_{0}$
and we denote by
![]() $\mathfrak{g}_{a}$
the
$\mathfrak{g}_{a}$
the
![]() $n$
-dimensional solvable Lie algebra with basis elements
$n$
-dimensional solvable Lie algebra with basis elements
![]() $Y_{0},X,Y_{2},\ldots ,Y_{n}$
and Lie brackets
$Y_{0},X,Y_{2},\ldots ,Y_{n}$
and Lie brackets
In particular sending
![]() $Y_{i}$
to
$Y_{i}$
to
![]() $Y_{i}$
and
$Y_{i}$
and
![]() $X$
to
$X$
to
![]() $Y_{0}^{-1}X_{1}$
we obtain the isomorphism
$Y_{0}^{-1}X_{1}$
we obtain the isomorphism
We now state the main result of this section.
Theorem 8.3. The algebra
![]() $R(n,a)$
satisfies the DME for any
$R(n,a)$
satisfies the DME for any
![]() $a\in \Bbbk$
and
$a\in \Bbbk$
and
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
The proof of Theorem 8.3 relies on the following lemmas.
Lemma 8.4. Let
![]() $P\in \operatorname{Spec}R$
and suppose that
$P\in \operatorname{Spec}R$
and suppose that
![]() $X_{0}\in P$
. Then
$X_{0}\in P$
. Then
![]() $P$
is locally closed in
$P$
is locally closed in
![]() $\operatorname{Spec}R$
if and only if
$\operatorname{Spec}R$
if and only if
![]() $P/\langle X_{0}\rangle$
is locally closed in
$P/\langle X_{0}\rangle$
is locally closed in
![]() $\operatorname{Spec}R/\langle X_{0}\rangle$
.
$\operatorname{Spec}R/\langle X_{0}\rangle$
.
Proof. This follows from the isomorphism
![]() $(R/\langle X_{0}\rangle )/(P/\langle X_{0}\rangle )\cong R/P$
.◻
$(R/\langle X_{0}\rangle )/(P/\langle X_{0}\rangle )\cong R/P$
.◻
For
![]() $P\in \operatorname{Spec}R$
with
$P\in \operatorname{Spec}R$
with
![]() $X_{0}\notin P$
, we set
$X_{0}\notin P$
, we set
![]() $P^{\circ }:=P[X_{0}^{-1}]\in \operatorname{Spec}R^{\circ }$
.
$P^{\circ }:=P[X_{0}^{-1}]\in \operatorname{Spec}R^{\circ }$
.
Lemma 8.5. Let
![]() $P\in \operatorname{Spec}R$
and suppose that
$P\in \operatorname{Spec}R$
and suppose that
![]() $X_{0}\notin P$
. Then
$X_{0}\notin P$
. Then
![]() $P$
is locally closed in
$P$
is locally closed in
![]() $\operatorname{Spec}R$
if and only if
$\operatorname{Spec}R$
if and only if
![]() $P^{\circ }$
is locally closed in
$P^{\circ }$
is locally closed in
![]() $\operatorname{Spec}R^{\circ }$
.
$\operatorname{Spec}R^{\circ }$
.
Proof. It is enough to prove the lemma for
![]() $P=\langle 0\rangle$
. Recall that
$P=\langle 0\rangle$
. Recall that
![]() $\langle 0\rangle$
is locally closed if and only if
$\langle 0\rangle$
is locally closed if and only if
![]() $\langle 0\rangle \neq \bigcap \{Q\in \operatorname{Spec}R\mid Q\neq \langle 0\rangle \}$
. We set
$\langle 0\rangle \neq \bigcap \{Q\in \operatorname{Spec}R\mid Q\neq \langle 0\rangle \}$
. We set
Suppose that
![]() ${\mathcal{I}}_{1}\neq \langle 0\rangle$
and let
${\mathcal{I}}_{1}\neq \langle 0\rangle$
and let
![]() $\langle 0\rangle \neq U\in {\mathcal{I}}_{1}$
. Then
$\langle 0\rangle \neq U\in {\mathcal{I}}_{1}$
. Then
![]() $U\in {\mathcal{I}}_{2}$
and
$U\in {\mathcal{I}}_{2}$
and
![]() ${\mathcal{I}}_{2}\neq 0$
. Reciprocally if
${\mathcal{I}}_{2}\neq 0$
. Reciprocally if
![]() ${\mathcal{I}}_{2}\neq \langle 0\rangle$
, then there exists
${\mathcal{I}}_{2}\neq \langle 0\rangle$
, then there exists
![]() $U$
nonzero inside
$U$
nonzero inside
![]() $\bigcap _{\langle 0\rangle \neq Q\in \operatorname{Spec}R~\text{and }X_{0}\notin Q}Q$
(recall that prime ideals are completely prime in
$\bigcap _{\langle 0\rangle \neq Q\in \operatorname{Spec}R~\text{and }X_{0}\notin Q}Q$
(recall that prime ideals are completely prime in
![]() $R$
, see assertion (1) of Theorem 7.1). Then
$R$
, see assertion (1) of Theorem 7.1). Then
![]() $UX_{0}$
belongs to any nonzero
$UX_{0}$
belongs to any nonzero
![]() $Q\in \operatorname{Spec}R$
and
$Q\in \operatorname{Spec}R$
and
![]() ${\mathcal{I}}_{1}\neq \langle 0\rangle$
.◻
${\mathcal{I}}_{1}\neq \langle 0\rangle$
.◻
We can now prove Theorem 8.3.
Proof of Theorem 8.3.
We proceed by induction on
![]() $n$
. It is well known that the Jordan plane
$n$
. It is well known that the Jordan plane
![]() $R(1,a)$
(
$R(1,a)$
(
![]() $a\neq 0$
) and the commutative polynomial ring
$a\neq 0$
) and the commutative polynomial ring
![]() $R(1,0)$
satisfy the DME, so that the base case
$R(1,0)$
satisfy the DME, so that the base case
![]() $n=1$
is true. Suppose that
$n=1$
is true. Suppose that
![]() $R(n-1,b)$
satisfies the DME for any
$R(n-1,b)$
satisfies the DME for any
![]() $b\in \Bbbk$
and
$b\in \Bbbk$
and
![]() $n>1$
. By [Reference Brown and GoodearlBG02, II.7.17] the algebra
$n>1$
. By [Reference Brown and GoodearlBG02, II.7.17] the algebra
![]() $R$
satisfies the (noncommutative) Nullstellensatz. Then by [Reference Brown and GoodearlBG02, II.7.15] we have the implications locally closed
$R$
satisfies the (noncommutative) Nullstellensatz. Then by [Reference Brown and GoodearlBG02, II.7.15] we have the implications locally closed
![]() $\Rightarrow$
primitive
$\Rightarrow$
primitive
![]() $\Rightarrow$
rational. It remains to prove that rational implies locally closed.
$\Rightarrow$
rational. It remains to prove that rational implies locally closed.
Let
![]() $P\in \operatorname{Spec}R$
be rational. Suppose first that
$P\in \operatorname{Spec}R$
be rational. Suppose first that
![]() $X_{0}\in P$
. Then
$X_{0}\in P$
. Then
and
![]() $P/\langle X_{0}\rangle$
is rational in
$P/\langle X_{0}\rangle$
is rational in
![]() $R/\langle X_{0}\rangle$
. Since
$R/\langle X_{0}\rangle$
. Since
![]() $R/\langle X_{0}\rangle \cong R(n-1,a+1)$
satisfies the DME by the induction hypothesis, the prime
$R/\langle X_{0}\rangle \cong R(n-1,a+1)$
satisfies the DME by the induction hypothesis, the prime
![]() $P/\langle X_{0}\rangle$
is locally closed. We conclude that
$P/\langle X_{0}\rangle$
is locally closed. We conclude that
![]() $P$
is locally closed by Lemma 8.4.
$P$
is locally closed by Lemma 8.4.
Suppose now that
![]() $X_{0}\notin P$
. Then
$X_{0}\notin P$
. Then
and
![]() $P^{\circ }$
is rational in
$P^{\circ }$
is rational in
![]() $R^{\circ }$
. Since the algebra
$R^{\circ }$
. Since the algebra
![]() $U(\mathfrak{g}_{a})$
satisfies the DME over
$U(\mathfrak{g}_{a})$
satisfies the DME over
![]() $\Bbbk$
by [Reference Irving and SmallIS80], the localization
$\Bbbk$
by [Reference Irving and SmallIS80], the localization
![]() $U(\mathfrak{g}_{a})[X_{0}^{-1}]\cong R^{\circ }$
satisfies the DME. Then
$U(\mathfrak{g}_{a})[X_{0}^{-1}]\cong R^{\circ }$
satisfies the DME. Then
![]() $P^{\circ }$
is locally closed in
$P^{\circ }$
is locally closed in
![]() $\operatorname{Spec}R^{\circ }$
and we conclude that
$\operatorname{Spec}R^{\circ }$
and we conclude that
![]() $P$
is locally closed in
$P$
is locally closed in
![]() $\operatorname{Spec}R$
by Lemma 8.5.◻
$\operatorname{Spec}R$
by Lemma 8.5.◻
The second main theorem of the section is that
![]() $A(n,a)$
satisfies the Poisson Dixmier–Moeglin equivalence, which we define here. Recall from Section 7 that a Poisson primitive ideal is by definition the largest Poisson ideal contained inside a maximal ideal. Let
$A(n,a)$
satisfies the Poisson Dixmier–Moeglin equivalence, which we define here. Recall from Section 7 that a Poisson primitive ideal is by definition the largest Poisson ideal contained inside a maximal ideal. Let
![]() $A$
be a Poisson
$A$
be a Poisson
![]() $\Bbbk$
-algebra and
$\Bbbk$
-algebra and
![]() $P\in \operatorname{PSpec}(A)$
. The ideal
$P\in \operatorname{PSpec}(A)$
. The ideal
![]() $P$
is said locally closed if the point
$P$
is said locally closed if the point
![]() $\{P\}$
is a locally closed point of
$\{P\}$
is a locally closed point of
![]() $\operatorname{PSpec}(A)$
and is said Poisson rational provided the field
$\operatorname{PSpec}(A)$
and is said Poisson rational provided the field
![]() $Z_{P}\big(\operatorname{Frac}(A/P)\big)$
is algebraic over the ground field
$Z_{P}\big(\operatorname{Frac}(A/P)\big)$
is algebraic over the ground field
![]() $\Bbbk$
. We say that the Poisson Dixmier–Moeglin equivalence holds for the Poisson algebra
$\Bbbk$
. We say that the Poisson Dixmier–Moeglin equivalence holds for the Poisson algebra
![]() $A$
if the sets of Poisson primitive ideals, of locally closed Poisson ideals and of Poisson rational ideals coincide. Our proof proceeds via a transfer result for the PDME.
$A$
if the sets of Poisson primitive ideals, of locally closed Poisson ideals and of Poisson rational ideals coincide. Our proof proceeds via a transfer result for the PDME.
Theorem 8.6. The algebra
![]() $A(n,a)$
satisfies the PDME for any
$A(n,a)$
satisfies the PDME for any
![]() $a\in \Bbbk$
and
$a\in \Bbbk$
and
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
Recall that we set
![]() $A^{\circ }:=A[X_{0}^{-1}]$
. We first prove two lemmas. An algebra is catenary if for every pair of distinct prime ideals
$A^{\circ }:=A[X_{0}^{-1}]$
. We first prove two lemmas. An algebra is catenary if for every pair of distinct prime ideals
![]() $P\subset Q$
all saturated chains of prime ideals from
$P\subset Q$
all saturated chains of prime ideals from
![]() $P$
to
$P$
to
![]() $Q$
have the same length.
$Q$
have the same length.
Lemma 8.7. Let
![]() $S$
be a catenary and Noetherian
$S$
be a catenary and Noetherian
![]() $\Bbbk$
-algebra with finite GK dimension and let
$\Bbbk$
-algebra with finite GK dimension and let
![]() $P\in \operatorname{Spec}S$
. Then
$P\in \operatorname{Spec}S$
. Then
where
![]() $ht(P)$
is the height of
$ht(P)$
is the height of
![]() $P$
, that is, the supremum of the length of chains of prime ideals descending from
$P$
, that is, the supremum of the length of chains of prime ideals descending from
![]() $P$
.
$P$
.
Proof. Since
![]() $S$
is catenary we can assume that
$S$
is catenary we can assume that
![]() $P=\langle 0\rangle$
. Suppose that
$P=\langle 0\rangle$
. Suppose that
![]() $S$
has only finitely many height one prime ideals, namely,
$S$
has only finitely many height one prime ideals, namely,
![]() $P_{1},\ldots ,P_{\ell }$
. Since
$P_{1},\ldots ,P_{\ell }$
. Since
![]() $S$
has finite GK dimension, it satisfies the DCC on prime ideals. In particular any nonzero
$S$
has finite GK dimension, it satisfies the DCC on prime ideals. In particular any nonzero
![]() $P\in \operatorname{Spec}S$
contains one of the
$P\in \operatorname{Spec}S$
contains one of the
![]() $P_{i}$
and therefore
$P_{i}$
and therefore
![]() $\{\langle 0\rangle \}=\operatorname{Spec}S\setminus V(\cap _{i}P_{i})$
is open in its closure.◻
$\{\langle 0\rangle \}=\operatorname{Spec}S\setminus V(\cap _{i}P_{i})$
is open in its closure.◻
Lemma 8.8. The ring
![]() $R=R(n,a)$
is catenary for any
$R=R(n,a)$
is catenary for any
![]() $a\in \Bbbk$
and
$a\in \Bbbk$
and
![]() $n\in \mathbb{Z}_{{>}0}$
.
$n\in \mathbb{Z}_{{>}0}$
.
Proof. Thanks to [Reference Brown and GoodearlBG02, II.9.5], Lemma 3.6 and the proof of Theorem 3.8, we only need to prove that
![]() $\operatorname{Spec}R$
has normal separation, that is, for every distinct pair
$\operatorname{Spec}R$
has normal separation, that is, for every distinct pair
![]() $P\subset Q$
of comparable primes in
$P\subset Q$
of comparable primes in
![]() $R$
the ideal
$R$
the ideal
![]() $Q/P$
of
$Q/P$
of
![]() $R/P$
contains a nonzero normal element of
$R/P$
contains a nonzero normal element of
![]() $R/P$
.
$R/P$
.
We proceed by induction on
![]() $n$
. Let
$n$
. Let
![]() $P\subset Q$
be a pair of comparable primes in
$P\subset Q$
be a pair of comparable primes in
![]() $R$
. The proof split into three cases.
$R$
. The proof split into three cases.
First assume that
![]() $X_{0}\in P$
, so that
$X_{0}\in P$
, so that
![]() $X_{0}\in Q$
. Then
$X_{0}\in Q$
. Then
![]() $P/\langle X_{0}\rangle \subset Q/\langle X_{0}\rangle$
inside
$P/\langle X_{0}\rangle \subset Q/\langle X_{0}\rangle$
inside
![]() $R/\langle X_{0}\rangle \cong R(n-1,a+1)$
, and we are done by induction.
$R/\langle X_{0}\rangle \cong R(n-1,a+1)$
, and we are done by induction.
Next assume that
![]() $X_{0}\notin Q$
, so that
$X_{0}\notin Q$
, so that
![]() $X_{0}\notin P$
. Then
$X_{0}\notin P$
. Then
![]() $P^{\circ }\subset Q^{\circ }$
inside
$P^{\circ }\subset Q^{\circ }$
inside
![]() $R^{\circ }\cong U(\mathfrak{g}_{a})[X_{0}^{-1}]$
. Since
$R^{\circ }\cong U(\mathfrak{g}_{a})[X_{0}^{-1}]$
. Since
![]() $\mathfrak{g}_{a}$
is solvable
$\mathfrak{g}_{a}$
is solvable
![]() $\operatorname{Spec}U(\mathfrak{g}_{a})$
has normal separation by [Reference Goodearl and WarfieldGW89, Theorem 12.19]. It is then easy to see that
$\operatorname{Spec}U(\mathfrak{g}_{a})$
has normal separation by [Reference Goodearl and WarfieldGW89, Theorem 12.19]. It is then easy to see that
![]() $\operatorname{Spec}U(\mathfrak{g}_{a})[X_{0}^{-1}]\cong R^{\circ }$
has normal separation. Hence there exists a nonzero normal element
$\operatorname{Spec}U(\mathfrak{g}_{a})[X_{0}^{-1}]\cong R^{\circ }$
has normal separation. Hence there exists a nonzero normal element
![]() $U$
in
$U$
in
![]() $Q^{\circ }/P^{\circ }\cong Q/P[X_{0}^{-1}]$
(where we denote again by
$Q^{\circ }/P^{\circ }\cong Q/P[X_{0}^{-1}]$
(where we denote again by
![]() $X_{0}$
its image in the quotient
$X_{0}$
its image in the quotient
![]() $Q/P$
). In particular there is an integer
$Q/P$
). In particular there is an integer
![]() $\ell \geqslant 0$
such that
$\ell \geqslant 0$
such that
![]() $UX_{0}^{\ell }$
is a nonzero normal element in
$UX_{0}^{\ell }$
is a nonzero normal element in
![]() $Q/P$
(recall that
$Q/P$
(recall that
![]() $X_{0}$
is normal in
$X_{0}$
is normal in
![]() $R$
).
$R$
).
Finally suppose that
![]() $X_{0}\notin P$
and
$X_{0}\notin P$
and
![]() $X_{0}\in Q$
. Then
$X_{0}\in Q$
. Then
![]() $X_{0}\in Q\setminus P$
and is normal modulo
$X_{0}\in Q\setminus P$
and is normal modulo
![]() $P$
as it is already normal in
$P$
as it is already normal in
![]() $R$
.◻
$R$
.◻
We now prove Theorem 8.6.
Proof of Theorem 8.6.
By [Reference OhOh99, Propositions 1.7, 1.10] we have the implications Poisson locally closed
![]() $\Rightarrow$
Poisson primitive
$\Rightarrow$
Poisson primitive
![]() $\Rightarrow$
Poisson rational. Let
$\Rightarrow$
Poisson rational. Let
![]() $P$
be a Poisson rational ideal of
$P$
be a Poisson rational ideal of
![]() $A$
. Then by [Reference Bell, Launois, Leon Sanchez and MoosaBLLM, Theorem 8.3] the set
$A$
. Then by [Reference Bell, Launois, Leon Sanchez and MoosaBLLM, Theorem 8.3] the set
![]() $\left\{Q\in \operatorname{PSpec}A~|~ht(Q)=ht(P)+1\right\}$
is finite. Since
$\left\{Q\in \operatorname{PSpec}A~|~ht(Q)=ht(P)+1\right\}$
is finite. Since
![]() $\operatorname{PSpec}A=\operatorname{Spec}R$
, the set
$\operatorname{PSpec}A=\operatorname{Spec}R$
, the set
is finite. By Lemma 8.7 we conclude that
![]() $P$
is locally closed in
$P$
is locally closed in
![]() $\operatorname{Spec}R$
, hence
$\operatorname{Spec}R$
, hence
![]() $P$
is locally closed in
$P$
is locally closed in
![]() $\operatorname{PSpec}A$
since
$\operatorname{PSpec}A$
since
![]() $\operatorname{PSpec}A=\operatorname{Spec}R$
.◻
$\operatorname{PSpec}A=\operatorname{Spec}R$
.◻
To end the section we investigate the structure of the skewfield of fractions
![]() $\operatorname{Frac}R$
of the Noetherian domain
$\operatorname{Frac}R$
of the Noetherian domain
![]() $R$
.
$R$
.
Recall the definition of the solvable Lie algebra
![]() $\mathfrak{g}_{a}$
from (8.1). By Equation (8.2),
$\mathfrak{g}_{a}$
from (8.1). By Equation (8.2),
![]() $R^{\circ }$
is isomorphic to a localization of the enveloping algebra
$R^{\circ }$
is isomorphic to a localization of the enveloping algebra
![]() $U(\mathfrak{g}_{a})$
. Then by [Reference Borho, Gabriel and RentschlerBGR73, Reference JosephJos77, Reference McConnellMcC74], the skewfield
$U(\mathfrak{g}_{a})$
. Then by [Reference Borho, Gabriel and RentschlerBGR73, Reference JosephJos77, Reference McConnellMcC74], the skewfield
![]() $\operatorname{Frac}R$
is isomorphic to a Weyl skewfield, when
$\operatorname{Frac}R$
is isomorphic to a Weyl skewfield, when
![]() $\Bbbk$
is algebraically closed and when the Lie algebra
$\Bbbk$
is algebraically closed and when the Lie algebra
![]() $\mathfrak{g}_{a}$
is algebraic. From [Reference Gelfand and KirillovGK66, Section 8] we note that this algebra is algebraic if and only if
$\mathfrak{g}_{a}$
is algebraic. From [Reference Gelfand and KirillovGK66, Section 8] we note that this algebra is algebraic if and only if
![]() $a\in \mathbb{Q}$
. In that case we provide an explicit description of this Weyl skewfield, and we show that
$a\in \mathbb{Q}$
. In that case we provide an explicit description of this Weyl skewfield, and we show that
![]() $\operatorname{Frac}R$
is not isomorphic to a Weyl skewfield when
$\operatorname{Frac}R$
is not isomorphic to a Weyl skewfield when
![]() $a\notin \mathbb{Q}$
. Moreover, we prove these results over a field of characteristic zero that is not necessarily algebraically closed. Recall that
$a\notin \mathbb{Q}$
. Moreover, we prove these results over a field of characteristic zero that is not necessarily algebraically closed. Recall that
![]() $R^{\circ }=B[X_{1};X_{0}\unicode[STIX]{x1D6E4}_{a}]$
, where
$R^{\circ }=B[X_{1};X_{0}\unicode[STIX]{x1D6E4}_{a}]$
, where
![]() $B=\Bbbk [X_{0}^{\pm 1},Y_{2},\ldots ,Y_{n}]$
.
$B=\Bbbk [X_{0}^{\pm 1},Y_{2},\ldots ,Y_{n}]$
.
For any field
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D700},a\in K$
, let
$\unicode[STIX]{x1D700},a\in K$
, let
![]() $\mathfrak{h}_{\unicode[STIX]{x1D700},a}(K)$
be the
$\mathfrak{h}_{\unicode[STIX]{x1D700},a}(K)$
be the
![]() $3$
-dimensional solvable Lie algebra over
$3$
-dimensional solvable Lie algebra over
![]() $K$
with basis
$K$
with basis
![]() $\{x,y,z\}$
and Lie bracket
$\{x,y,z\}$
and Lie bracket
![]() $[x,y]=\unicode[STIX]{x1D700}y$
,
$[x,y]=\unicode[STIX]{x1D700}y$
,
![]() $[x,z]=az$
and
$[x,z]=az$
and
![]() $[y,z]=0$
.
$[y,z]=0$
.
Proposition 8.9. We have
![]() $\operatorname{Frac}R\cong \operatorname{Frac}U(\mathfrak{g}_{a})\cong \operatorname{Frac}U(\mathfrak{h}_{\unicode[STIX]{x1D716},a}(K))$
where
$\operatorname{Frac}R\cong \operatorname{Frac}U(\mathfrak{g}_{a})\cong \operatorname{Frac}U(\mathfrak{h}_{\unicode[STIX]{x1D716},a}(K))$
where
![]() $K=\big(Q_{gr}(B)\big)_{0}$
is a field of transcendence degree
$K=\big(Q_{gr}(B)\big)_{0}$
is a field of transcendence degree
![]() $n-2$
over
$n-2$
over
![]() $\Bbbk$
, and where
$\Bbbk$
, and where
![]() $\unicode[STIX]{x1D700}=2$
if
$\unicode[STIX]{x1D700}=2$
if
![]() $n=2$
and
$n=2$
and
![]() $\unicode[STIX]{x1D700}=1$
if
$\unicode[STIX]{x1D700}=1$
if
![]() $n>2$
.
$n>2$
.
Proof. We define a
![]() $\mathbb{Z}^{2}$
-grading
$\mathbb{Z}^{2}$
-grading
![]() $f$
on
$f$
on
![]() $B$
as follows. Set
$B$
as follows. Set
![]() $f(X_{1}^{\pm 1})=(\pm 1,0)$
and
$f(X_{1}^{\pm 1})=(\pm 1,0)$
and
![]() $f(Y_{i})=(1,i)$
for all
$f(Y_{i})=(1,i)$
for all
![]() $i=2,\ldots ,n$
. This is a combination of the
$i=2,\ldots ,n$
. This is a combination of the
![]() $d$
-grading and the
$d$
-grading and the
![]() $\unicode[STIX]{x1D716}$
-grading. Note that if
$\unicode[STIX]{x1D716}$
-grading. Note that if
![]() $u\in B$
has degree
$u\in B$
has degree
![]() $(0,0)$
, then
$(0,0)$
, then
![]() $u\in \ker \unicode[STIX]{x1D6E4}_{a}$
. We now form the graded quotient ring
$u\in \ker \unicode[STIX]{x1D6E4}_{a}$
. We now form the graded quotient ring
![]() $E:=Q_{gr}(B)$
of
$E:=Q_{gr}(B)$
of
![]() $B$
by inverting all its homogeneous elements
$B$
by inverting all its homogeneous elements
Note that
![]() $E$
is also
$E$
is also
![]() $\mathbb{Z}^{2}$
-graded by a grading denoted
$\mathbb{Z}^{2}$
-graded by a grading denoted
![]() $f$
again. It is a standard fact that
$f$
again. It is a standard fact that
![]() $E\cong K[s^{\pm 1},t^{\pm 1}]$
, where
$E\cong K[s^{\pm 1},t^{\pm 1}]$
, where
![]() $K=E_{(0,0)}$
is a field such that
$K=E_{(0,0)}$
is a field such that
and where
![]() $0\neq s\in E_{(1,0)}$
and
$0\neq s\in E_{(1,0)}$
and
![]() $0\neq t\in E_{(0,\unicode[STIX]{x1D700})}$
. By definition
$0\neq t\in E_{(0,\unicode[STIX]{x1D700})}$
. By definition
![]() $\unicode[STIX]{x1D700}:=\min \{\unicode[STIX]{x1D6FC}\geqslant 1~|~E_{(0,\unicode[STIX]{x1D6FC})}\neq 0\}$
. For instance we can choose
$\unicode[STIX]{x1D700}:=\min \{\unicode[STIX]{x1D6FC}\geqslant 1~|~E_{(0,\unicode[STIX]{x1D6FC})}\neq 0\}$
. For instance we can choose
![]() $s=X_{0}$
and
$s=X_{0}$
and
![]() $t=Y_{2}X_{0}^{-1}$
when
$t=Y_{2}X_{0}^{-1}$
when
![]() $n=2$
, or
$n=2$
, or
![]() $t=Y_{3}Y_{2}^{-1}$
when
$t=Y_{3}Y_{2}^{-1}$
when
![]() $n>2$
. Thus we have
$n>2$
. Thus we have
For
![]() $u\in K$
we have
$u\in K$
we have
![]() $X_{1}u-uX_{1}=\unicode[STIX]{x1D6E4}_{a}(u)=0$
since
$X_{1}u-uX_{1}=\unicode[STIX]{x1D6E4}_{a}(u)=0$
since
![]() $f(u)=(0,0)$
, and
$f(u)=(0,0)$
, and
![]() $u$
commutes also with
$u$
commutes also with
![]() $s$
and
$s$
and
![]() $t$
since
$t$
since
![]() $E$
is commutative. Moreover, we get
$E$
is commutative. Moreover, we get
We conclude by setting
![]() $X_{1}^{\prime }:=X_{1}X_{0}^{-1}$
that
$X_{1}^{\prime }:=X_{1}X_{0}^{-1}$
that
![]() $X_{1}^{\prime }s-sX_{1}^{\prime }=aX_{0}=as$
and
$X_{1}^{\prime }s-sX_{1}^{\prime }=aX_{0}=as$
and
![]() $X_{1}^{\prime }t-tX_{1}^{\prime }=\unicode[STIX]{x1D700}t$
. Since
$X_{1}^{\prime }t-tX_{1}^{\prime }=\unicode[STIX]{x1D700}t$
. Since
![]() $s,t\in B$
we have
$s,t\in B$
we have
![]() $st=ts$
and the result follows by setting
$st=ts$
and the result follows by setting
![]() $x:=X_{1}^{\prime }$
,
$x:=X_{1}^{\prime }$
,
![]() $y:=t$
and
$y:=t$
and
![]() $z:=s$
.◻
$z:=s$
.◻
Remark 8.10. Generators of the field
![]() $K$
can be obtained by solving the system of equations
$K$
can be obtained by solving the system of equations
Setting
![]() $Y_{0}:=X_{0}$
and
$Y_{0}:=X_{0}$
and
![]() $Z_{i}:=Y_{i}Y_{n-1}^{-(n-i)}Y_{n}^{n-i-1}$
for
$Z_{i}:=Y_{i}Y_{n-1}^{-(n-i)}Y_{n}^{n-i-1}$
for
![]() $i\in \{0,2,\ldots ,n-2\}$
we have
$i\in \{0,2,\ldots ,n-2\}$
we have
![]() $K=\Bbbk \left(Z_{0},Z_{2},\ldots ,Z_{n-2}\right)$
. Note that
$K=\Bbbk \left(Z_{0},Z_{2},\ldots ,Z_{n-2}\right)$
. Note that
![]() $K$
is purely transcendental over
$K$
is purely transcendental over
![]() $\Bbbk$
of transcendence degree
$\Bbbk$
of transcendence degree
![]() $n-2$
.
$n-2$
.
Theorem 8.11. When
![]() $a\in \mathbb{Q}$
the skewfield
$a\in \mathbb{Q}$
the skewfield
![]() $\operatorname{Frac}R$
is isomorphic to the first Weyl skewfield
$\operatorname{Frac}R$
is isomorphic to the first Weyl skewfield
![]() $D_{1}(F)$
over a field
$D_{1}(F)$
over a field
![]() $F$
of transcendence degree
$F$
of transcendence degree
![]() $n-1$
over
$n-1$
over
![]() $\Bbbk$
. When
$\Bbbk$
. When
![]() $a\notin \mathbb{Q}$
, we have
$a\notin \mathbb{Q}$
, we have
![]() $Z(\operatorname{Frac}R)=K$
, and
$Z(\operatorname{Frac}R)=K$
, and
![]() $\operatorname{Frac}R$
is not isomorphic to any Weyl skewfield.
$\operatorname{Frac}R$
is not isomorphic to any Weyl skewfield.
Proof. The skewfield of the enveloping algebra of the Lie algebra
![]() $\mathfrak{h}_{\unicode[STIX]{x1D700},a}(\Bbbk )$
is either isomorphic to the first Weyl skewfield over a field of transcendence degree 1 over
$\mathfrak{h}_{\unicode[STIX]{x1D700},a}(\Bbbk )$
is either isomorphic to the first Weyl skewfield over a field of transcendence degree 1 over
![]() $\Bbbk$
when
$\Bbbk$
when
![]() $a$
is rational, or has a trivial center when
$a$
is rational, or has a trivial center when
![]() $a$
is irrational. This is a classical fact that can be found in [Reference Gelfand and KirillovGK66, Section 8] and [Reference RichardRic02, Proposition 1.2.4.1 and Remark after]. The result follows from Proposition 8.9 and the isomorphism
$a$
is irrational. This is a classical fact that can be found in [Reference Gelfand and KirillovGK66, Section 8] and [Reference RichardRic02, Proposition 1.2.4.1 and Remark after]. The result follows from Proposition 8.9 and the isomorphism
![]() $U(\mathfrak{h}_{\unicode[STIX]{x1D700},a}(K))\cong U(\mathfrak{h}_{\unicode[STIX]{x1D700},a}(\Bbbk ))\otimes _{\Bbbk }K$
.◻
$U(\mathfrak{h}_{\unicode[STIX]{x1D700},a}(K))\cong U(\mathfrak{h}_{\unicode[STIX]{x1D700},a}(\Bbbk ))\otimes _{\Bbbk }K$
.◻
Remarks 8.12.
(1) Let
 $a\in \mathbb{Q}$
and suppose that
$a\in \mathbb{Q}$
and suppose that
 $a=p/q\in \mathbb{Q}$
with
$a=p/q\in \mathbb{Q}$
with
 $\gcd (p,q)=1$
(when
$\gcd (p,q)=1$
(when
 $a=0$
we have
$a=0$
we have
 $p=0$
and we set
$p=0$
and we set
 $q=1$
). Setting
$q=1$
). Setting
 $Z:=X_{0}^{q}Y_{2}^{p}Y_{3}^{-p}$
we obtain where the
$Z:=X_{0}^{q}Y_{2}^{p}Y_{3}^{-p}$
we obtain where the $$\begin{eqnarray}F=\Bbbk (Z,Z_{0},Z_{1},\ldots ,Z_{n-2})\end{eqnarray}$$
$$\begin{eqnarray}F=\Bbbk (Z,Z_{0},Z_{1},\ldots ,Z_{n-2})\end{eqnarray}$$
 $Z_{i}$
’s are defined in Remark 8.10.
$Z_{i}$
’s are defined in Remark 8.10.(2) For
 $a,b\in \mathbb{Q}$
it is clear that
$a,b\in \mathbb{Q}$
it is clear that
 $\operatorname{Frac}R(n,a)\cong \operatorname{Frac}R(n,b)$
since both are isomorphic to a Weyl skewfield over a field of transcendence degree
$\operatorname{Frac}R(n,a)\cong \operatorname{Frac}R(n,b)$
since both are isomorphic to a Weyl skewfield over a field of transcendence degree
 $n-2$
. When
$n-2$
. When
 $a\notin \mathbb{Q}$
and
$a\notin \mathbb{Q}$
and
 $b=\pm a+n$
for some
$b=\pm a+n$
for some
 $n\in \mathbb{Z}$
, it is easy to verify that the skewfields
$n\in \mathbb{Z}$
, it is easy to verify that the skewfields
 $\operatorname{Frac}R(n,a)$
and
$\operatorname{Frac}R(n,a)$
and
 $\operatorname{Frac}R(n,b)$
are isomorphic. However, it remains unclear whether or not this condition is also necessary for an isomorphism
$\operatorname{Frac}R(n,b)$
are isomorphic. However, it remains unclear whether or not this condition is also necessary for an isomorphism
 $\operatorname{Frac}R(n,a)\cong \operatorname{Frac}R(n,b)$
when
$\operatorname{Frac}R(n,a)\cong \operatorname{Frac}R(n,b)$
when
 $a,b\notin \mathbb{Q}$
.
$a,b\notin \mathbb{Q}$
.
Using similar methods we can prove the following result about the Poisson structure of the field
![]() $\operatorname{Frac}(A)$
. For a Lie algebra
$\operatorname{Frac}(A)$
. For a Lie algebra
![]() $\mathfrak{g}$
we denote by
$\mathfrak{g}$
we denote by
![]() $S(\mathfrak{g})$
its symmetric algebra that we endow with the so-called Kirillov–Kostant–Souriau Poisson bracket, that is the Poisson bracket obtained by extending by bi-derivation and bi-linearity the Lie bracket of
$S(\mathfrak{g})$
its symmetric algebra that we endow with the so-called Kirillov–Kostant–Souriau Poisson bracket, that is the Poisson bracket obtained by extending by bi-derivation and bi-linearity the Lie bracket of
![]() $\mathfrak{g}$
inside
$\mathfrak{g}$
inside
![]() $S(\mathfrak{g})$
$S(\mathfrak{g})$
for any
![]() $X,Y\in \mathfrak{g}$
.
$X,Y\in \mathfrak{g}$
.
Theorem 8.13. As Poisson algebras, we have
![]() $\operatorname{Frac}A\cong \operatorname{Frac}S(\mathfrak{g}_{a})\cong \operatorname{Frac}S(\mathfrak{h}_{\unicode[STIX]{x1D700},a}(K))$
. Moreover, if
$\operatorname{Frac}A\cong \operatorname{Frac}S(\mathfrak{g}_{a})\cong \operatorname{Frac}S(\mathfrak{h}_{\unicode[STIX]{x1D700},a}(K))$
. Moreover, if
![]() $a\in \mathbb{Q}$
then
$a\in \mathbb{Q}$
then
![]() $\operatorname{Frac}A$
is isomorphic to the field of fractions of the Poisson algebra
$\operatorname{Frac}A$
is isomorphic to the field of fractions of the Poisson algebra
![]() ${\mathcal{P}}=F[X,Y]$
, where
${\mathcal{P}}=F[X,Y]$
, where
![]() $\{X,Y\}=1$
and where
$\{X,Y\}=1$
and where
![]() $F$
is the field described in Remark 8.12. When
$F$
is the field described in Remark 8.12. When
![]() $a\notin \mathbb{Q}$
, the Poisson center of
$a\notin \mathbb{Q}$
, the Poisson center of
![]() $\operatorname{Frac}A$
is
$\operatorname{Frac}A$
is
![]() $K$
and
$K$
and
![]() $\operatorname{Frac}A$
is not isomorphic to
$\operatorname{Frac}A$
is not isomorphic to
![]() $\operatorname{Frac}{\mathcal{P}}$
.
$\operatorname{Frac}{\mathcal{P}}$
.
9 Examples of spectra
In this final section we study
![]() $\operatorname{PSpec}A(n,a)$
and
$\operatorname{PSpec}A(n,a)$
and
![]() $\operatorname{Spec}R(n,a)$
for small values of
$\operatorname{Spec}R(n,a)$
for small values of
![]() $n$
. Since these two spectra are equal it is enough to describe
$n$
. Since these two spectra are equal it is enough to describe
![]() $\operatorname{PSpec}A(n,a)$
. Because we give explicit description of these spectra we assume that
$\operatorname{PSpec}A(n,a)$
. Because we give explicit description of these spectra we assume that
![]() $\Bbbk$
is algebraically closed in this section.
$\Bbbk$
is algebraically closed in this section.
Example 9.1. Let
![]() $n=1$
and consider
$n=1$
and consider
![]() $A=A(1,a)$
. If
$A=A(1,a)$
. If
![]() $a=0$
then
$a=0$
then
![]() $A(1,a)=\Bbbk [X_{0},X_{1}]$
with trivial Poisson bracket and thus
$A(1,a)=\Bbbk [X_{0},X_{1}]$
with trivial Poisson bracket and thus
Suppose that
![]() $a\neq 0$
. Then
$a\neq 0$
. Then
![]() $A$
is isomorphic to the Poisson–Jordan plane (see Example 3.16). It is well known that its Poisson spectrum is
$A$
is isomorphic to the Poisson–Jordan plane (see Example 3.16). It is well known that its Poisson spectrum is
and that the
![]() $d$
-graded primes are
$d$
-graded primes are
![]() $\langle X_{0}\rangle ,\langle X_{0},X_{1}\rangle$
. Moreover, only
$\langle X_{0}\rangle ,\langle X_{0},X_{1}\rangle$
. Moreover, only
![]() $\langle X_{0}\rangle$
is not Poisson primitive.
$\langle X_{0}\rangle$
is not Poisson primitive.
Assume that
![]() $n\geqslant 2$
and that
$n\geqslant 2$
and that
![]() $a\in \mathbb{Q}^{\times }$
. We denote by
$a\in \mathbb{Q}^{\times }$
. We denote by
![]() $\operatorname{PSpec}_{1}A(n,a)$
the set of Poisson prime ideals of
$\operatorname{PSpec}_{1}A(n,a)$
the set of Poisson prime ideals of
![]() $A$
that contain
$A$
that contain
![]() $X_{0}$
and by
$X_{0}$
and by
![]() $\operatorname{PSpec}_{0}A(n,a)$
the set of Poisson prime ideals of
$\operatorname{PSpec}_{0}A(n,a)$
the set of Poisson prime ideals of
![]() $A$
that do not contain
$A$
that do not contain
![]() $X_{0}$
. Since
$X_{0}$
. Since
![]() $A(n,a)/\langle X_{0}\rangle \cong A(n-1,a+1)$
by Proposition 3.7 there is a homeomorphism:
$A(n,a)/\langle X_{0}\rangle \cong A(n-1,a+1)$
by Proposition 3.7 there is a homeomorphism:
On the other hand by Theorem 7.5 there is a homeomorphism
where
![]() $Z$
is the Poisson center of
$Z$
is the Poisson center of
![]() $A^{\circ }=A(n,a)[X_{0}^{-1}]$
. Thus to describe
$A^{\circ }=A(n,a)[X_{0}^{-1}]$
. Thus to describe
![]() $\operatorname{PSpec}A(n,a)$
completely we must study the ring
$\operatorname{PSpec}A(n,a)$
completely we must study the ring
![]() $Z$
. We know that
$Z$
. We know that
![]() $\operatorname{Kdim}Z=n-1$
, so we first construct
$\operatorname{Kdim}Z=n-1$
, so we first construct
![]() $n-1$
algebraically independent elements of
$n-1$
algebraically independent elements of
![]() $Z$
.
$Z$
.
Write
![]() $a=p/q$
with
$a=p/q$
with
![]() $\gcd (p,q)=1$
and
$\gcd (p,q)=1$
and
![]() $-p>0$
. For
$-p>0$
. For
![]() $i=2,\ldots ,n$
let
$i=2,\ldots ,n$
let
![]() $d_{i}=\gcd (p,i)>0$
, and set
$d_{i}=\gcd (p,i)>0$
, and set
![]() $u_{i}=p+iq/d_{i}$
and
$u_{i}=p+iq/d_{i}$
and
![]() $v_{i}=-p/d_{i}$
. Note that
$v_{i}=-p/d_{i}$
. Note that
![]() $\gcd (u_{i},v_{i})=1$
. Finally we set
$\gcd (u_{i},v_{i})=1$
. Finally we set
By construction
![]() $e(Y_{i}^{\prime })=0$
, and we have
$e(Y_{i}^{\prime })=0$
, and we have
![]() $Z^{\prime }:=\Bbbk [Y_{2}^{\prime },\ldots ,Y_{n}^{\prime }]\subseteq Z$
.
$Z^{\prime }:=\Bbbk [Y_{2}^{\prime },\ldots ,Y_{n}^{\prime }]\subseteq Z$
.
We can be more precise
Lemma 9.3.
![]() $Z$
is a free
$Z$
is a free
![]() $Z^{\prime }$
-module with basis
$Z^{\prime }$
-module with basis
In particular its rank is
![]() $|S|\leqslant \prod _{i=2}^{n}v_{i}$
.
$|S|\leqslant \prod _{i=2}^{n}v_{i}$
.
Proof. By the extension of Proposition 3.21 to
![]() $A^{\circ }$
we have
$A^{\circ }$
we have
![]() $Z=(A^{\circ })^{\unicode[STIX]{x1D6E4}_{a},\unicode[STIX]{x1D6E5}}=B_{0}$
and so
$Z=(A^{\circ })^{\unicode[STIX]{x1D6E4}_{a},\unicode[STIX]{x1D6E5}}=B_{0}$
and so
 $$\begin{eqnarray}\displaystyle Z & = & \displaystyle \text{Span}\left\{\vphantom{\mathop{\sum }_{i=2}^{n}}X_{0}^{s}Y_{2}^{s_{2}}\cdots Y_{n}^{s_{n}}~|~s\in \mathbb{Z},~s_{2},\ldots ,s_{n}\in \mathbb{N},~\text{and}~as\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\mathop{\sum }_{i=2}^{n}(a+i)s_{i}=0\right\}\nonumber\\ \displaystyle & = & \displaystyle \text{Span}\left\{\vphantom{\mathop{\sum }_{i=2}^{n}}X_{0}^{s}Y_{2}^{s_{2}}\cdots Y_{n}^{s_{n}}~|~s\in \mathbb{Z},~s_{2},\ldots ,s_{n}\in \mathbb{N},~\text{and}~ps\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\mathop{\sum }_{i=2}^{n}u_{i}d_{i}s_{i}=0\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z & = & \displaystyle \text{Span}\left\{\vphantom{\mathop{\sum }_{i=2}^{n}}X_{0}^{s}Y_{2}^{s_{2}}\cdots Y_{n}^{s_{n}}~|~s\in \mathbb{Z},~s_{2},\ldots ,s_{n}\in \mathbb{N},~\text{and}~as\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\mathop{\sum }_{i=2}^{n}(a+i)s_{i}=0\right\}\nonumber\\ \displaystyle & = & \displaystyle \text{Span}\left\{\vphantom{\mathop{\sum }_{i=2}^{n}}X_{0}^{s}Y_{2}^{s_{2}}\cdots Y_{n}^{s_{n}}~|~s\in \mathbb{Z},~s_{2},\ldots ,s_{n}\in \mathbb{N},~\text{and}~ps\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\mathop{\sum }_{i=2}^{n}u_{i}d_{i}s_{i}=0\right\}.\nonumber\end{eqnarray}$$
Let
![]() $M=X_{0}^{s}Y_{2}^{s_{2}}\cdots Y_{n}^{s_{n}}\in Z$
and for
$M=X_{0}^{s}Y_{2}^{s_{2}}\cdots Y_{n}^{s_{n}}\in Z$
and for
![]() $i=2,\ldots ,n$
set
$i=2,\ldots ,n$
set
![]() $s_{i}=v_{i}s_{i}^{\prime }+\unicode[STIX]{x1D700}_{i}$
, where
$s_{i}=v_{i}s_{i}^{\prime }+\unicode[STIX]{x1D700}_{i}$
, where
![]() $s_{i}^{\prime }\geqslant 0$
and
$s_{i}^{\prime }\geqslant 0$
and
![]() $0\leqslant \unicode[STIX]{x1D700}_{i}<v_{i}$
. Then we rewrite
$0\leqslant \unicode[STIX]{x1D700}_{i}<v_{i}$
. Then we rewrite
where
![]() $\unicode[STIX]{x1D6FA}=\sum _{i=2}^{n}s_{i}^{\prime }u_{i}$
. Since
$\unicode[STIX]{x1D6FA}=\sum _{i=2}^{n}s_{i}^{\prime }u_{i}$
. Since
![]() $M,Y_{2}^{\prime s_{2}^{\prime }}\cdots Y_{n}^{\prime s_{n}^{\prime }}\in Z^{\prime }$
we have
$M,Y_{2}^{\prime s_{2}^{\prime }}\cdots Y_{n}^{\prime s_{n}^{\prime }}\in Z^{\prime }$
we have
![]() $X_{0}^{s-\unicode[STIX]{x1D6FA}}Y_{2}^{\unicode[STIX]{x1D700}_{2}}\cdots Y_{n}^{\unicode[STIX]{x1D700}_{n}}\in Z$
. In particular this shows that a generating set of
$X_{0}^{s-\unicode[STIX]{x1D6FA}}Y_{2}^{\unicode[STIX]{x1D700}_{2}}\cdots Y_{n}^{\unicode[STIX]{x1D700}_{n}}\in Z$
. In particular this shows that a generating set of
![]() $Z$
as a module over
$Z$
as a module over
![]() $Z^{\prime }$
is given by the set
$Z^{\prime }$
is given by the set
![]() $S$
. The result follows since the elements of
$S$
. The result follows since the elements of
![]() $S$
are linearly independent over
$S$
are linearly independent over
![]() $Z^{\prime }$
.◻
$Z^{\prime }$
.◻
Note that it is possible that
![]() $S=\{1\}$
. For example, let
$S=\{1\}$
. For example, let
![]() $n=2$
and set
$n=2$
and set
![]() $M=X_{0}^{s}Y_{2}^{s_{2}}\in S$
. Then
$M=X_{0}^{s}Y_{2}^{s_{2}}\in S$
. Then
![]() $ps+u_{2}d_{2}s_{2}=0$
, that is,
$ps+u_{2}d_{2}s_{2}=0$
, that is,
![]() $v_{2}s=u_{2}s_{2}$
and
$v_{2}s=u_{2}s_{2}$
and
![]() $v_{2}$
must divide
$v_{2}$
must divide
![]() $s_{2}$
since
$s_{2}$
since
![]() $\gcd (u_{2},v_{2})=1$
. This implies that
$\gcd (u_{2},v_{2})=1$
. This implies that
![]() $s_{2}=0$
since
$s_{2}=0$
since
![]() $0\leqslant s_{2}<v_{2}$
. Therefore,
$0\leqslant s_{2}<v_{2}$
. Therefore,
![]() $Z=Z^{\prime }=\Bbbk [Y_{2}^{\prime }]$
when
$Z=Z^{\prime }=\Bbbk [Y_{2}^{\prime }]$
when
![]() $n=2$
.
$n=2$
.
We next work out
![]() $\operatorname{PSpec}A(2,a)$
explicitly. By Example 9.1, for
$\operatorname{PSpec}A(2,a)$
explicitly. By Example 9.1, for
![]() $a,b\in \mathbb{Q}\smallsetminus \{-1\}$
the sets
$a,b\in \mathbb{Q}\smallsetminus \{-1\}$
the sets
![]() $\operatorname{PSpec}_{1}A(2,a)$
and
$\operatorname{PSpec}_{1}A(2,a)$
and
![]() $\operatorname{PSpec}_{1}A(2,b)$
are homeomorphic. More precisely we have
$\operatorname{PSpec}_{1}A(2,b)$
are homeomorphic. More precisely we have
The following result explicitly describes the stratum
![]() $\operatorname{PSpec}_{0}A(2,a)$
.
$\operatorname{PSpec}_{0}A(2,a)$
.
Proposition 9.5. For
![]() $a\in \mathbb{Q}^{\times }$
we have
$a\in \mathbb{Q}^{\times }$
we have
![]() $\operatorname{PSpec}_{0}A(2,a)=\{\!\langle 0\rangle ,\langle X_{0}Y_{2}\rangle ,P_{\unicode[STIX]{x1D706}}~|~\unicode[STIX]{x1D706}\in \Bbbk ^{\times }\!\}$
, where
$\operatorname{PSpec}_{0}A(2,a)=\{\!\langle 0\rangle ,\langle X_{0}Y_{2}\rangle ,P_{\unicode[STIX]{x1D706}}~|~\unicode[STIX]{x1D706}\in \Bbbk ^{\times }\!\}$
, where
The ideal
![]() $P_{\unicode[STIX]{x1D706}}$
is Poisson maximal if and only if
$P_{\unicode[STIX]{x1D706}}$
is Poisson maximal if and only if
![]() $-1<a<0$
.
$-1<a<0$
.
Proof. Let
![]() $A=A(2,a)$
and let
$A=A(2,a)$
and let
![]() $A^{\circ }=A[X_{0}^{-1}]$
. Let
$A^{\circ }=A[X_{0}^{-1}]$
. Let
![]() $Z$
be the Poisson center of
$Z$
be the Poisson center of
![]() $A^{\circ }$
. Recall from the discussion after Lemma 9.3 that
$A^{\circ }$
. Recall from the discussion after Lemma 9.3 that
![]() $Z=\Bbbk [Y_{2}^{\prime }]$
where
$Z=\Bbbk [Y_{2}^{\prime }]$
where
![]() $Y_{2}^{\prime }=X_{0}^{u_{2}}Y_{2}^{v_{2}}$
. We denote by
$Y_{2}^{\prime }=X_{0}^{u_{2}}Y_{2}^{v_{2}}$
. We denote by
![]() $\unicode[STIX]{x1D711}$
the bijection between
$\unicode[STIX]{x1D711}$
the bijection between
![]() $\operatorname{Spec}Z$
and
$\operatorname{Spec}Z$
and
![]() $\operatorname{PSpec}_{0}A$
sending
$\operatorname{PSpec}_{0}A$
sending
![]() $Q\in \operatorname{Spec}Z$
to
$Q\in \operatorname{Spec}Z$
to
![]() $\unicode[STIX]{x1D711}(Q)=\sqrt{QA^{\circ }}\cap A$
. It is clear that
$\unicode[STIX]{x1D711}(Q)=\sqrt{QA^{\circ }}\cap A$
. It is clear that
![]() $\unicode[STIX]{x1D711}(Y_{2}^{\prime }Z)=\langle X_{0}Y_{2}\rangle$
. If
$\unicode[STIX]{x1D711}(Y_{2}^{\prime }Z)=\langle X_{0}Y_{2}\rangle$
. If
![]() $\unicode[STIX]{x1D706}\neq 0$
, the ideal
$\unicode[STIX]{x1D706}\neq 0$
, the ideal
![]() $(Y_{2}^{\prime }-\unicode[STIX]{x1D706})A^{\circ }$
of
$(Y_{2}^{\prime }-\unicode[STIX]{x1D706})A^{\circ }$
of
![]() $A^{\circ }$
is prime and so
$A^{\circ }$
is prime and so
![]() $\unicode[STIX]{x1D711}((Y_{2}^{\prime }-\unicode[STIX]{x1D706})Z)=\big((Y_{2}^{\prime }-\unicode[STIX]{x1D706})A^{\circ }\big)\cap A$
. Since
$\unicode[STIX]{x1D711}((Y_{2}^{\prime }-\unicode[STIX]{x1D706})Z)=\big((Y_{2}^{\prime }-\unicode[STIX]{x1D706})A^{\circ }\big)\cap A$
. Since
![]() $Y_{2}^{\prime }=X_{0}^{u_{2}-v_{2}}(X_{0}Y_{2})^{v_{2}}$
, we have
$Y_{2}^{\prime }=X_{0}^{u_{2}-v_{2}}(X_{0}Y_{2})^{v_{2}}$
, we have
But
![]() $u_{2}-v_{2}=\frac{2}{d_{2}}(p+q)$
and we have:
$u_{2}-v_{2}=\frac{2}{d_{2}}(p+q)$
and we have:
Thus
![]() $\operatorname{PSpec}A$
is as described.
$\operatorname{PSpec}A$
is as described.
If
![]() $-1<a<0$
then
$-1<a<0$
then
![]() $u_{2}-v_{2}>0$
and
$u_{2}-v_{2}>0$
and
![]() $P_{\unicode[STIX]{x1D706}}=\langle X_{0}^{u_{2}-v_{2}}(X_{0}Y_{2})^{v_{2}}-\unicode[STIX]{x1D706}\rangle$
is comaximal with
$P_{\unicode[STIX]{x1D706}}=\langle X_{0}^{u_{2}-v_{2}}(X_{0}Y_{2})^{v_{2}}-\unicode[STIX]{x1D706}\rangle$
is comaximal with
![]() $X_{0}$
and thus with all primes in
$X_{0}$
and thus with all primes in
![]() $\operatorname{PSpec}_{1}(A)$
. If
$\operatorname{PSpec}_{1}(A)$
. If
![]() $a=-1$
then
$a=-1$
then
![]() $P_{\unicode[STIX]{x1D706}}=\langle X_{0}X_{2}-X_{1}^{2}/2-\unicode[STIX]{x1D706}\rangle$
is contained in the Poisson ideal
$P_{\unicode[STIX]{x1D706}}=\langle X_{0}X_{2}-X_{1}^{2}/2-\unicode[STIX]{x1D706}\rangle$
is contained in the Poisson ideal
![]() $\langle X_{0},X_{1}^{2}/2-\unicode[STIX]{x1D706}\rangle$
. If
$\langle X_{0},X_{1}^{2}/2-\unicode[STIX]{x1D706}\rangle$
. If
![]() $a<-1$
or
$a<-1$
or
![]() $a>0$
then
$a>0$
then
![]() $v_{2}-u_{2}>0$
and
$v_{2}-u_{2}>0$
and
![]() $P_{\unicode[STIX]{x1D706}}$
is clearly contained in
$P_{\unicode[STIX]{x1D706}}$
is clearly contained in
![]() $\langle X_{0},X_{1}\rangle$
.◻
$\langle X_{0},X_{1}\rangle$
.◻
We deduce the following result.
Theorem 9.7. Let
![]() $a\in \mathbb{Q}^{\times }\smallsetminus \{-1\}$
. Then we have
$a\in \mathbb{Q}^{\times }\smallsetminus \{-1\}$
. Then we have
where the ideals
![]() $P_{\unicode[STIX]{x1D706}}$
are described in Proposition 9.5. Moreover, only
$P_{\unicode[STIX]{x1D706}}$
are described in Proposition 9.5. Moreover, only
![]() $\langle 0\rangle$
and
$\langle 0\rangle$
and
![]() $\langle X_{0},X_{1}\rangle$
are not Poisson primitive. Further,
$\langle X_{0},X_{1}\rangle$
are not Poisson primitive. Further,
![]() $\operatorname{PSpec}A(2,a)$
is homeomorphic to
$\operatorname{PSpec}A(2,a)$
is homeomorphic to
![]() $\operatorname{PSpec}A(2,b)$
if and only if
$\operatorname{PSpec}A(2,b)$
if and only if
![]() $(a^{2}+a)/(b^{2}+b)>0$
.
$(a^{2}+a)/(b^{2}+b)>0$
.
Proof. The description of
![]() $\operatorname{PSpec}A(2,a)$
is immediate from Proposition 9.5. Pictorially,
$\operatorname{PSpec}A(2,a)$
is immediate from Proposition 9.5. Pictorially,
![]() $\operatorname{PSpec}A(2,a)$
is given by the following diagrams, where lines represent inclusion of ideals.
$\operatorname{PSpec}A(2,a)$
is given by the following diagrams, where lines represent inclusion of ideals.

Note that despite the fact that the algebras
![]() $A(2,a)$
are not isomorphic for different values of
$A(2,a)$
are not isomorphic for different values of
![]() $a$
(see Theorem 5.1), their spectra fall generically into only two nonhomeomorphic families.
$a$
(see Theorem 5.1), their spectra fall generically into only two nonhomeomorphic families.
Since the topology on
![]() $\operatorname{PSpec}A(2,a)$
is governed by inclusions, it is clear that
$\operatorname{PSpec}A(2,a)$
is governed by inclusions, it is clear that
![]() $\operatorname{PSpec}A(2,a)$
and
$\operatorname{PSpec}A(2,a)$
and
![]() $\operatorname{PSpec}A(2,b)$
are homeomorphic if and only if
$\operatorname{PSpec}A(2,b)$
are homeomorphic if and only if
![]() $a,b$
fall into the same case of (9.6), which is if and only if
$a,b$
fall into the same case of (9.6), which is if and only if
![]() $(a^{2}+a)/(b^{2}+b)>0$
.◻
$(a^{2}+a)/(b^{2}+b)>0$
.◻
Example 9.8. Let
![]() $a=1/2$
. Then
$a=1/2$
. Then
![]() $p=-1$
,
$p=-1$
,
![]() $q=-2$
,
$q=-2$
,
![]() $d_{2}=1$
,
$d_{2}=1$
,
![]() $u_{2}=-5$
and
$u_{2}=-5$
and
![]() $v_{2}=1$
. Thus
$v_{2}=1$
. Thus
On the other hand when
![]() $a=-1/2$
we have
$a=-1/2$
we have
![]() $p=-1$
,
$p=-1$
,
![]() $q=2$
,
$q=2$
,
![]() $d_{2}=1$
,
$d_{2}=1$
,
![]() $u_{2}=3$
and
$u_{2}=3$
and
![]() $v_{2}=1$
. Thus
$v_{2}=1$
. Thus
which is Poisson maximal. Therefore, the two spectra are not homeomorphic.
Remark 9.9. From Theorem 7.5, when
![]() $a\not \in \mathbb{Q}$
then
$a\not \in \mathbb{Q}$
then
Note that these are the prime ideals that are Poisson for all values of
![]() $a$
.
$a$
.
For all
![]() $a\neq -1,0$
there are five
$a\neq -1,0$
there are five
![]() $d$
-graded Poisson primes of
$d$
-graded Poisson primes of
![]() $A(2,a)$
: the ideals
$A(2,a)$
: the ideals
For the remainder of this section, we study
![]() $\operatorname{PSpec}A(3,a)$
for various values of
$\operatorname{PSpec}A(3,a)$
for various values of
![]() $a$
. Again, we are most interested in
$a$
. Again, we are most interested in
![]() $\operatorname{PSpec}_{0}A(3,a)$
which is homeomorphic to
$\operatorname{PSpec}_{0}A(3,a)$
which is homeomorphic to
![]() $\operatorname{Spec}Z$
as above. From Lemma 9.3 we know that
$\operatorname{Spec}Z$
as above. From Lemma 9.3 we know that
![]() $Z$
is a free module over
$Z$
is a free module over
![]() $Z^{\prime }=\Bbbk [Y_{2}^{\prime },Y_{3}^{\prime }]$
with basis
$Z^{\prime }=\Bbbk [Y_{2}^{\prime },Y_{3}^{\prime }]$
with basis
Proposition 9.10. The cardinality of
![]() $S$
is equal to
$S$
is equal to
![]() $\unicode[STIX]{x1D6FC}:=-p/d_{2}d_{3}$
.
$\unicode[STIX]{x1D6FC}:=-p/d_{2}d_{3}$
.
Proof. Since
![]() $p=-d_{2}v_{2}=-d_{3}v_{3}$
the equation
$p=-d_{2}v_{2}=-d_{3}v_{3}$
the equation
![]() $ps+u_{2}d_{2}s_{2}+u_{3}d_{3}s_{3}=0$
implies that
$ps+u_{2}d_{2}s_{2}+u_{3}d_{3}s_{3}=0$
implies that
![]() $d_{2}$
divides
$d_{2}$
divides
![]() $s_{3}$
(since
$s_{3}$
(since
![]() $\gcd (d_{2},u_{3}d_{3})=1$
) and
$\gcd (d_{2},u_{3}d_{3})=1$
) and
![]() $d_{3}$
divides
$d_{3}$
divides
![]() $s_{2}$
(since
$s_{2}$
(since
![]() $\gcd (d_{3},u_{2}d_{2})=1$
). Set
$\gcd (d_{3},u_{2}d_{2})=1$
). Set
![]() $s_{2}:=k_{2}d_{3}$
and
$s_{2}:=k_{2}d_{3}$
and
![]() $s_{3}:=k_{3}d_{2}$
. Then the equation
$s_{3}:=k_{3}d_{2}$
. Then the equation
![]() $ps+u_{2}d_{2}s_{2}+u_{3}d_{3}s_{3}=0$
becomes
$ps+u_{2}d_{2}s_{2}+u_{3}d_{3}s_{3}=0$
becomes
To solve this Diophantine equation we first set
![]() $t=-\unicode[STIX]{x1D6FC}s+u_{2}k_{2}$
and we solve
$t=-\unicode[STIX]{x1D6FC}s+u_{2}k_{2}$
and we solve
![]() $t+u_{3}k_{3}=0$
. We get
$t+u_{3}k_{3}=0$
. We get
for
![]() $k\in \mathbb{Z}$
. We now solve the Diophantine equation
$k\in \mathbb{Z}$
. We now solve the Diophantine equation
![]() $-\unicode[STIX]{x1D6FC}s+u_{2}k_{2}=t=-u_{3}k$
. Since
$-\unicode[STIX]{x1D6FC}s+u_{2}k_{2}=t=-u_{3}k$
. Since
![]() $\gcd (-\unicode[STIX]{x1D6FC},u_{2})=1$
there exist
$\gcd (-\unicode[STIX]{x1D6FC},u_{2})=1$
there exist
![]() $m,n\in \mathbb{Z}$
such that
$m,n\in \mathbb{Z}$
such that
![]() $-\unicode[STIX]{x1D6FC}m+u_{2}n=1$
. The solution of the equation
$-\unicode[STIX]{x1D6FC}m+u_{2}n=1$
. The solution of the equation
![]() $-\unicode[STIX]{x1D6FC}s+u_{2}k_{2}=-u_{3}k$
is then
$-\unicode[STIX]{x1D6FC}s+u_{2}k_{2}=-u_{3}k$
is then
for
![]() $k,\ell \in \mathbb{Z}$
, and the solution of (9.11) is
$k,\ell \in \mathbb{Z}$
, and the solution of (9.11) is
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}s=-mu_{3}k+u_{2}\ell ,\quad \\ k_{2}=-nu_{3}k+\unicode[STIX]{x1D6FC}\ell ,\quad \\ k_{3}=k,\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}s=-mu_{3}k+u_{2}\ell ,\quad \\ k_{2}=-nu_{3}k+\unicode[STIX]{x1D6FC}\ell ,\quad \\ k_{3}=k,\quad \end{array}\right.\end{eqnarray}$$
for
![]() $k,\ell \in \mathbb{Z}$
.
$k,\ell \in \mathbb{Z}$
.
For
![]() $i=2,3$
we have
$i=2,3$
we have
![]() $0\leqslant k_{i}<\unicode[STIX]{x1D6FC}=-p/d_{2}d_{3}$
since
$0\leqslant k_{i}<\unicode[STIX]{x1D6FC}=-p/d_{2}d_{3}$
since
![]() $0\leqslant s_{i}<v_{i}$
. Fix
$0\leqslant s_{i}<v_{i}$
. Fix
![]() $k_{3}\in \{0,\ldots ,\unicode[STIX]{x1D6FC}-1\}$
. Since
$k_{3}\in \{0,\ldots ,\unicode[STIX]{x1D6FC}-1\}$
. Since
![]() $k_{2}=-nu_{3}k_{3}+\unicode[STIX]{x1D6FC}\ell$
for some
$k_{2}=-nu_{3}k_{3}+\unicode[STIX]{x1D6FC}\ell$
for some
![]() $\ell \in \mathbb{Z}$
, there exists a unique
$\ell \in \mathbb{Z}$
, there exists a unique
![]() $\ell \in \mathbb{Z}$
such that
$\ell \in \mathbb{Z}$
such that
![]() $k_{2}\in \{0,\ldots ,\unicode[STIX]{x1D6FC}-1\}$
. The integer
$k_{2}\in \{0,\ldots ,\unicode[STIX]{x1D6FC}-1\}$
. The integer
![]() $s$
is uniquely determined by
$s$
is uniquely determined by
![]() $k_{2}$
and
$k_{2}$
and
![]() $k_{3}$
, so we conclude that to each
$k_{3}$
, so we conclude that to each
![]() $k_{3}\in \{0,\ldots ,\unicode[STIX]{x1D6FC}-1\}$
corresponds a unique monomial
$k_{3}\in \{0,\ldots ,\unicode[STIX]{x1D6FC}-1\}$
corresponds a unique monomial
![]() $X_{0}^{s}Y_{2}^{s_{2}}Y_{3}^{s_{3}}\in S$
.◻
$X_{0}^{s}Y_{2}^{s_{2}}Y_{3}^{s_{3}}\in S$
.◻
Since
![]() $\unicode[STIX]{x1D6FC}=1\;\Longleftrightarrow \;S=\{1\}$
we deduce the following corollary.
$\unicode[STIX]{x1D6FC}=1\;\Longleftrightarrow \;S=\{1\}$
we deduce the following corollary.
Corollary 9.13. We have
![]() $Z=Z^{\prime }$
if and only if
$Z=Z^{\prime }$
if and only if
![]() $\unicode[STIX]{x1D6FC}=1$
if and only if
$\unicode[STIX]{x1D6FC}=1$
if and only if
![]() $p\in \{-1,-2,-3,-6\}$
.
$p\in \{-1,-2,-3,-6\}$
.
From the proof of Proposition 9.10 we observe that
and that a recipe for finding these basis elements consists of computing
![]() $m,m^{\prime }$
such that
$m,m^{\prime }$
such that
![]() $-\unicode[STIX]{x1D6FC}m+u_{2}m^{\prime }=1$
, plugging these values into (9.12) and, for each
$-\unicode[STIX]{x1D6FC}m+u_{2}m^{\prime }=1$
, plugging these values into (9.12) and, for each
![]() $0\leqslant k_{3}<\unicode[STIX]{x1D6FC}$
, finding the unique
$0\leqslant k_{3}<\unicode[STIX]{x1D6FC}$
, finding the unique
![]() $l\in \mathbb{Z}$
such that
$l\in \mathbb{Z}$
such that
![]() $k_{2}=-m^{\prime }u_{3}k_{3}+\unicode[STIX]{x1D6FC}l\in \{0,\ldots ,\unicode[STIX]{x1D6FC}-1\}$
. We conclude this section with a couple of examples with
$k_{2}=-m^{\prime }u_{3}k_{3}+\unicode[STIX]{x1D6FC}l\in \{0,\ldots ,\unicode[STIX]{x1D6FC}-1\}$
. We conclude this section with a couple of examples with
![]() $\unicode[STIX]{x1D6FC}\neq 1$
which illustrate possibilities for the ring structure of
$\unicode[STIX]{x1D6FC}\neq 1$
which illustrate possibilities for the ring structure of
![]() $Z$
. But first we describe the
$Z$
. But first we describe the
![]() $d$
-graded Poisson prime that are common to
$d$
-graded Poisson prime that are common to
![]() $A(3,a)$
for any generic
$A(3,a)$
for any generic
![]() $a$
. By Theorem 7.5 we have
$a$
. By Theorem 7.5 we have
![]() $\operatorname{PSpec}_{\operatorname{gr}}A^{\circ }\cong \mathbb{P}_{k}(2,3)\sqcup \{(Y_{2},Y_{3})\}$
. In particular, for any
$\operatorname{PSpec}_{\operatorname{gr}}A^{\circ }\cong \mathbb{P}_{k}(2,3)\sqcup \{(Y_{2},Y_{3})\}$
. In particular, for any
![]() $[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}]\in \mathbb{P}^{1}$
, the element
$[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}]\in \mathbb{P}^{1}$
, the element
is Poisson central. Multiplying by
![]() $X_{0}^{6}$
, we obtain a pencil of Poisson normal sextic elements of
$X_{0}^{6}$
, we obtain a pencil of Poisson normal sextic elements of
![]() $A(4,a)$
$A(4,a)$
 $$\begin{eqnarray}\displaystyle X_{0}^{6}F_{[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}]} & = & \displaystyle \unicode[STIX]{x1D6FC}(X_{0}^{3}X_{2}^{3}-{\textstyle \frac{3}{2}}X_{0}^{2}X_{1}^{2}X_{2}^{2}+{\textstyle \frac{3}{4}}X_{0}X_{1}^{4}X_{2}-{\textstyle \frac{1}{8}}X_{1}^{6})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FD}(X_{0}^{4}X_{3}^{2}+X_{0}^{2}X_{1}^{2}X_{2}^{2}+{\textstyle \frac{1}{9}}X_{1}^{6}-2X_{0}^{3}X_{1}X_{2}X_{3}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{2}{3}}X_{0}^{2}X_{1}^{3}X_{3}-{\textstyle \frac{2}{3}}X_{0}X_{1}^{4}X_{2} )\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{0}^{6}F_{[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}]} & = & \displaystyle \unicode[STIX]{x1D6FC}(X_{0}^{3}X_{2}^{3}-{\textstyle \frac{3}{2}}X_{0}^{2}X_{1}^{2}X_{2}^{2}+{\textstyle \frac{3}{4}}X_{0}X_{1}^{4}X_{2}-{\textstyle \frac{1}{8}}X_{1}^{6})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FD}(X_{0}^{4}X_{3}^{2}+X_{0}^{2}X_{1}^{2}X_{2}^{2}+{\textstyle \frac{1}{9}}X_{1}^{6}-2X_{0}^{3}X_{1}X_{2}X_{3}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{2}{3}}X_{0}^{2}X_{1}^{3}X_{3}-{\textstyle \frac{2}{3}}X_{0}X_{1}^{4}X_{2} )\!.\nonumber\end{eqnarray}$$
Therefore, the
![]() $d$
-graded Poisson prime ideals that are common to
$d$
-graded Poisson prime ideals that are common to
![]() $A(3,a)$
for any
$A(3,a)$
for any
![]() $a\neq -2,-1,0$
are
$a\neq -2,-1,0$
are
Among them the Poisson primitive ideals are
![]() $\langle X_{0},X_{1}\rangle ,\langle X_{0}Y_{2},X_{0}^{2}Y_{3}\rangle$
and
$\langle X_{0},X_{1}\rangle ,\langle X_{0}Y_{2},X_{0}^{2}Y_{3}\rangle$
and
![]() $\langle X_{0},X_{1},X_{2}\rangle ,\langle X_{0},X_{1},X_{2},X_{3}\rangle$
.
$\langle X_{0},X_{1},X_{2}\rangle ,\langle X_{0},X_{1},X_{2},X_{3}\rangle$
.
Example 9.14. For
![]() $a=-5/4$
(the algebra in Example 1.1) we have
$a=-5/4$
(the algebra in Example 1.1) we have
![]() $\unicode[STIX]{x1D6FC}=5$
,
$\unicode[STIX]{x1D6FC}=5$
,
![]() $Y_{2}^{\prime }=X_{0}^{3}Y_{2}^{5}$
and
$Y_{2}^{\prime }=X_{0}^{3}Y_{2}^{5}$
and
![]() $Y_{3}^{\prime }=X_{0}^{7}Y_{3}^{5}$
. Moreover,
$Y_{3}^{\prime }=X_{0}^{7}Y_{3}^{5}$
. Moreover,
with
![]() $(X_{0}^{2}Y_{2}Y_{3})^{5}=Y_{2}^{\prime }Y_{3}^{\prime }$
. Thus
$(X_{0}^{2}Y_{2}Y_{3})^{5}=Y_{2}^{\prime }Y_{3}^{\prime }$
. Thus
![]() $Z\cong \Bbbk [A,B,C]/\langle C^{5}=AB\rangle$
.
$Z\cong \Bbbk [A,B,C]/\langle C^{5}=AB\rangle$
.
Example 9.15. Choose
![]() $a=-24/5$
. We have
$a=-24/5$
. We have
![]() $\unicode[STIX]{x1D6FC}=4$
,
$\unicode[STIX]{x1D6FC}=4$
,
![]() $Y_{2}^{\prime }=X_{0}^{-7}Y_{2}^{12}$
and
$Y_{2}^{\prime }=X_{0}^{-7}Y_{2}^{12}$
and
![]() $Y_{3}^{\prime }=X_{0}^{-3}Y_{2}^{8}$
. We have
$Y_{3}^{\prime }=X_{0}^{-3}Y_{2}^{8}$
. We have
![]() $S=\{1,C,D,E\}$
, where
$S=\{1,C,D,E\}$
, where
![]() $C:=X_{0}^{-4}Y_{2}^{3}Y_{3}^{6}$
,
$C:=X_{0}^{-4}Y_{2}^{3}Y_{3}^{6}$
,
![]() $D:=X_{0}^{-5}Y_{2}^{6}Y_{3}^{4}$
and
$D:=X_{0}^{-5}Y_{2}^{6}Y_{3}^{4}$
and
![]() $E:=X_{0}^{-6}Y_{2}^{9}Y_{3}^{2}$
. We further set
$E:=X_{0}^{-6}Y_{2}^{9}Y_{3}^{2}$
. We further set
![]() $A:=Y_{2}^{\prime }$
and
$A:=Y_{2}^{\prime }$
and
![]() $B:=Y_{3}^{\prime }$
. We have
$B:=Y_{3}^{\prime }$
. We have
Acknowledgments
We thank Michel Van den Bergh, François Dumas, Gene Freudenburg, and Diane Maclagan for helpful comments. We particularly thank Brent Pym for extremely useful discussion on a visit of Susan Sierra to Oxford in early 2016 (including suggesting that the algebras
![]() $R(n,a)$
are all twists of each other). This project began when Cesar Lecoutre was supported by an LMS mobility grant to visit the University of Edinburgh, and we thank the LMS and the University of Edinburgh for their support.
$R(n,a)$
are all twists of each other). This project began when Cesar Lecoutre was supported by an LMS mobility grant to visit the University of Edinburgh, and we thank the LMS and the University of Edinburgh for their support.
We thank the anonymous referee for their helpful comments.