Given a finite-dimensional Banach space 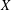 $X$ and an Auerbach basis
$X$ and an Auerbach basis 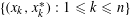 $\{(x_{k},x_{k}^{\ast }):1\leqslant k\leqslant n\}$ of
$\{(x_{k},x_{k}^{\ast }):1\leqslant k\leqslant n\}$ of 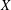 $X$, it is proved that there exist
$X$, it is proved that there exist 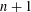 $n+1$ linear combinations
$n+1$ linear combinations 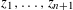 $z_{1},\ldots ,z_{n+1}$ of
$z_{1},\ldots ,z_{n+1}$ of 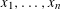 $x_{1},\ldots ,x_{n}$ with coordinates
$x_{1},\ldots ,x_{n}$ with coordinates 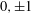 $0,\pm 1$, such that
$0,\pm 1$, such that 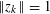 $\Vert z_{k}\Vert =1$, for
$\Vert z_{k}\Vert =1$, for 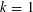 $k=1$,
$k=1$, 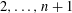 $2,\ldots ,n+1$ and
$2,\ldots ,n+1$ and 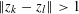 $\Vert z_{k}-z_{l}\Vert >1$, for
$\Vert z_{k}-z_{l}\Vert >1$, for 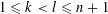 $1\leqslant k<l\leqslant n+1$.
$1\leqslant k<l\leqslant n+1$.
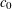 $c_{0}$ THEOREM
$c_{0}$ THEOREM
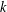 $k$ -TUPLES OF REDUCED RESIDUES
$k$ -TUPLES OF REDUCED RESIDUES