Published online by Cambridge University Press: 07 January 2015
This paper presents a recent result for the problem introduced eleven years ago by Fraenkel and McLeod [A diffusing vortex circle in a viscous fluid. In IUTAM Symposium on Asymptotics, Singularities and Homogenisation in Problems of Mechanics, Kluwer (2003), 489–500], but described only briefly there. We shall prove the following, as far as space allows. The vorticity 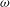 ${\it\omega}$ of a diffusing vortex circle in a viscous fluid has, for small values of a non-dimensional time, a second approximation
${\it\omega}$ of a diffusing vortex circle in a viscous fluid has, for small values of a non-dimensional time, a second approximation 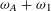 ${\it\omega}_{A}+{\it\omega}_{1}$ that, although formulated for a fixed, finite Reynolds number
${\it\omega}_{A}+{\it\omega}_{1}$ that, although formulated for a fixed, finite Reynolds number  ${\it\lambda}$ and exact for
${\it\lambda}$ and exact for 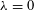 ${\it\lambda}=0$ (then
${\it\lambda}=0$ (then 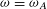 ${\it\omega}={\it\omega}_{A}$), tends to a smooth limiting function as
${\it\omega}={\it\omega}_{A}$), tends to a smooth limiting function as 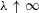 ${\it\lambda}\uparrow \infty$. In §§1 and 2 the necessary background and apparatus are described; §3 outlines the new result and its proof.
${\it\lambda}\uparrow \infty$. In §§1 and 2 the necessary background and apparatus are described; §3 outlines the new result and its proof.