Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T15:23:44.886Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE COMPUTATION OF HIGH-DIMENSIONAL POTENTIALS OF ADVECTION–DIFFUSION OPERATORS

Part of: Numerical approximation and computational geometry

Published online by Cambridge University Press:  24 February 2015

Flavia Lanzara  and
Gunther Schmidt
Flavia Lanzara
Affiliation:
Department of Mathematics, Sapienza University of Rome, Piazzale Aldo Moro 2, 00185 Rome, Italy email [email protected]
Gunther Schmidt
Affiliation:
Weierstrass Institute forApplied Analysis and Stochastics, Mohrenstrasse 39, 10117 Berlin, Germany email [email protected]
Get access

Abstract

We study a fast method for computing potentials of advection–diffusion operators $-{\rm\Delta}+2\mathbf{b}\boldsymbol{\cdot }{\rm\nabla}+c$ with 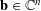$\mathbf{b}\in \mathbb{C}^{n}$ and 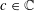$c\in \mathbb{C}$ over rectangular boxes in 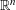$\mathbb{R}^{n}$. By combining high-order cubature formulas with modern methods of structured tensor product approximations, we derive an approximation of the potentials which is accurate and provides approximation formulas of high order. The cubature formulas have been obtained by using the basis functions introduced in the theory of approximate approximations. The action of volume potentials on the basis functions allows one-dimensional integral representations with separable integrands, i.e. a product of functions depending on only one of the variables. Then a separated representation of the density, combined with a suitable quadrature rule, leads to a tensor product representation of the integral operator. Since only one-dimensional operations are used, the resulting method is effective also in the high-dimensional case.

MSC classification

Primary: 65D32: Quadrature and cubature formulas
Type
Research Article
Information
Mathematika , Volume 61 , Issue 2 , May 2015 , pp. 309 - 327
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions, Dover (1968).Google Scholar
Beylkin, G. and Mohlenkamp, M. J., Numerical operator calculus in higher dimensions. Proc. Natl. Acad. Sci. USA 99 2002, 10246–10251.CrossRefGoogle ScholarPubMed
Beylkin, G. and Mohlenkamp, M. J., Algorithms for numerical analysis in high dimensions. SIAM J. Sci. Comput. 26 2005, 2133–2159.CrossRefGoogle Scholar
Hestenes, M. R., Extension of the range of differentiable functions. Duke Math. J. 8 1941, 183–192.CrossRefGoogle Scholar
John, F., Partial Differential Equations, 4th edn., Springer (1982).CrossRefGoogle Scholar
Khoromskij, B. N., Fast and accurate tensor approximation of a multivariate convolution with linear scaling in dimension. J. Comput. Appl. Math. 234 2010, 3122–3139.CrossRefGoogle Scholar
Lanzara, F., Maz’ya, V. and Schmidt, G., On the fast computation of high dimensional volume potentials. Math. Comp. 80 2011, 887–904.CrossRefGoogle Scholar
Lanzara, F., Maz’ya, V. and Schmidt, G., Accuracy cubature of volume potentials over high-dimensional half-spaces. J. Math. Sci. 173 2011, 683–700.CrossRefGoogle Scholar
Lanzara, F., Maz’ya, V. and Schmidt, G., Fast cubature of volume potentials over rectangular domains by approximate approximations. Appl. Comput. Harmon. Anal. 36 2014, 167–182.CrossRefGoogle Scholar
Maz’ya, V., Approximate Approximations (The Mathematics of Finite Elements and Applications. Highlights 1993) (ed. Whiteman, J. R.), Wiley (Chichester, 1994), 77–104.Google Scholar
Maz’ya, V., Sobolev Spaces with Applications to Elliptic Partial Differential Equations, Vol. 342, Springer (2011).CrossRefGoogle Scholar
Maz’ya, V. and Schmidt, G., Approximate Approximations (Mathematical Surveys and Monographs 141), American Mathematical Society (Providence, RI, 2007).CrossRefGoogle Scholar
Takahasi, H. and Mori, M., Double exponential formulas for numerical integration. Publ. Res. Inst. Math. Sci. Kyoto Univ. 9 1974, 721–741.CrossRefGoogle Scholar
Waldvogel, J., Towards a general error theory of the trapezoidal rule. Springer Optim. Appl. 42 2011, 267–282.Google Scholar