The compact–open topology for function spaces is usually attributed to R. H. Fox in 1945 [16]; and indeed, there is no earlier publication to attribute it to. But it is clear from Fox's paper that the idea of the compact–open topology, and its notable success in locally compact spaces, were already familiar. The topology of course goes back to Riemann; and to generalize to locally compact spaces needs only a definition or two. The actual contributions of Fox were (1) to formulate the partial result, and the problem of extending it, clearly and categorically; (2) to show that in separable metric spaces there is no extension beyond locally compact spaces; (3) to anticipate, partially and somewhat awkwardly, the idea of changing the category so as to save the functorial equation. (Scholarly reservations: Fox attributes the question to Hurewicz, and doubtless Hurewicz had a share in (1). As for (2), when Fox's paper was published R. Arens was completing a dissertation which gave a more general result [1] – though worse formulated.)

The publication of the hundredth volume of a learned journal is surely an appropriate excuse for a mild outbreak of retrospective self-congratulation, even if (as in the present case) the occasion does not coincide with any particular anniversary in the history of the journal. With this in mind, the Editorial Committee of Mathematical Proceedings have commissioned a number of survey articles by distinguished mathematicians, which will appear in this and the following two parts of volume 100; the purpose of this editorial is to sketch in the historical background and to introduce the survey articles.

In 1951 A. S. Besicovitch, who was my research supervisor, suggested that I look at the problem of determining the dimension of the range of a Brownian motion path. This problem had been communicated to him by C. Loewner, but it was a natural question which had already attracted the attention of Paul Lévy. It was a good problem to give to an ignorant Ph.D. student because it forced him to learn the potential theory of Frostman [33] and Riesz[75] as well as the Wiener [98] definition of mathematical Brownian motion. In fact the solution of that first problem in [81] used only ideas which were already twenty-five years old, though at the time they seemed both new and original to me. My purpose in this paper is to try to trace the development of these techniques as they have been exploited by many authors and used in diverse situations since 1953. As we do this in the limited space available it will be impossible to even outline all aspects of the development, so I make no apology for giving a biased account concentrating on those areas of most interest to me. At the same time I will make conjectures and suggest some problems which are natural and accessible in the hope of stimulating further research.

The object of this survey article is to trace the influence on the theory of modular forms of the ideas contained in L. J. Mordell's important paper ‘On Mr Ramanujan's empirical expansions of modular functions’, which appeared in October 1917 in this Society's Proceedings [32]. The equally important paper [42] by S. Ramanujan, ‘On certain arithmetical functions’, referred to in Mordell's title, was published in May 1916 in the same Society's older journal, the Transactions, which was regrettably suppressed in 1928, 107 years after its foundation. Ramanujan's paper was concerned not only with multiplicative properties of Fourier coefficients of modular forms, but also with their order of magnitude. Since subsequent papers on the latter subject have also appeared in the Proceedings, it seems appropriate to include further developments in this field of study in the present survey.

As a mathematical area generalized inversion1 was inaugurated in 1955 by R. Penrose [128]. Since then there have appeared about 2000 articles and 15 books2 on generalized inverses of matrices and linear operators. See the annotated bibliography by Nashed and Rall [121] for the period up to 1976.

In the paper ‘Bordism and Cobordism’, which appeared in vol. 57 (1961) of this journal [5], Michael Atiyah introduced and began the study of bordism and cobordism theory. The present article will trace developments in this area since this beginning.

Let k be a field of zero characteristic, and let F be a function field over k of genus g. We normalize each valuation v on F so that its order group consists of all rational integers, and for elements u1, …, un of F, not all zero, we define the (projective) height as

The sum formula on F shows that this is really a height on the projective space .

Sturm's theorem was announced in 1829 and various proofs were given soon after (see [2], p. 363 for details). It is given in various textbooks on algebra, e.g. in [1], pp. 448–453, where its application to finding the number and location of the real zeros of a polynomial is explained. It has been applied, in conjunction with Givens's method, to finding the eigenvalues of a matrix (see, e.g. [3], p. 494), and has been used recently in a neat computational form by Takeuchi [4] for investigating algebraic fields.

0. Mordell proved his ‘Finite Basis Theorem’ in the paper [31] ‘On the rational solutions of the indeterminate equations of the third and fourth degrees’ which appeared in 1922 in Volume 21 of these Proceedings. It had been assumed, rather than conjectured, by Poincaré some 20 years previously, but it was not what he had set out to prove. The theorem and its generalizations are at the heart of many of the most interesting achievements and problems of the theory of numbers and also of algebraic geometry. Mordell himself had virtually no part in these developments: his great work was to lie elsewhere ([5]).

When a familiar notion is modelled in a certain topos E, the natural problem arises to what extent theorems concerning its models in usual set theory remain valid for its models in E, or how suitable properties of E affect the validity of certain of these theorems. Problems of this type have in particular been studied by Banaschewski[2], Bhutani[5], and Ebrahimi[6, 7], dealing with abelian groups in a localic topos and universal algebra in an arbitrary Grothendieck topos. 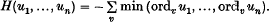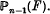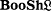This paper is concerned with Boolean algebras, specifically with injectivity and related topics for the category of Boolean algebras in the topos 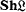of sheaves on a locale 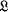and with properties of the initial Boolean algebra in .

Let λ(n) denote the Liouville function, i.e. λ(n) = 1 if n has an even number of prime factors, and λ(n) = − 1 otherwise. It is natural to expect that the sequence λ(n) (n ≥ 1) behaves like a random sequence of ± signs. In particular, it seems highly plausible that for any choice of εi = ± 1 (i = 0,…, k) we have

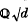In this paper we continue the study of elliptic curves defined over a quadratic field with good reduction at primes not dividing 2 begun in [9] (referred to as I). We extend the results of I to show that such a curve must have a point of order 2 also defined over when d = −7, −3, −2, −1, 2, 3 or 5 and list all such curves over .

Throughout this paper k will be an algebraically closed field, R the ring k[[X1, …, XN]] and (kN, 0) the k-scheme Spec(R).

Let K be an algebraic number field and f(X) ∈ K[X]. The Diophantine problem of describing the solutions to equations of the form

has attracted considerable interest over the past 60 years. Siegel [12], [13] was the first to show that under suitable non-degeneracy conditions, the equation (+) has only finitely many integral solutions in K. LeVeque[7] proved the following, more explicit, result. Let

where a ∈ K* and αl,…,αk are distinct and algebraic over K. Then (+) has only finitely many integral solutions unless (nl,…,nk) is a permutation of one of the n-tuples

In this paper we develop a descent technique for generalized (co)-homology theories defined in the category of algebraic varieties. By such a theory we mean a functor Sch→C, where C is a closed model category in the sense of Quillen satisfying certain axioms (cf. §4). We have chosen to work in such a general context so as to include two situations for which the results of SGA 4 of Deligne and Saint-Donat are not applicable: descent of multiplicative structures (i.e. of differential graded algebras) and descent for generalized sheaf cohomology (such as the algebraic K-theory of coherent sheaves over a noetherian scheme).

Let Top be the category of compactly generated topological spaces and continuous maps. The category, Top, can be given the structure of a simplicially enriched category (or S-category, S being the category of simplicial sets). For A a small category, Vogt (in [22]) constructed a category, Coh (A, Top), of homotopy coherent A-indexed diagrams in Top and homotopy classes of homotopy coherent maps, and proved a theorem identifying this as being equivalent to Ho (TopA), the category obtained from the category of commutative A-indexed diagrams by localizing with respect to the level homotopy equivalences. Thus one of the important consequences of Vogt's result is that it provides concrete coherent models for the formal composites of maps and formal inverses of level homotopy equivalences which are the maps in Ho (TopA). The usefulness of such models and in general of Vogt's results is shown in the series of notes [14–17] by the second author in which those results are applied to give an obstruction theory applicable in prohomotopy theory.

Envelopes of hypersurfaces arise in many different geometric situations. For example, the canal surfaces associated with a space curve can be obtained as the envelope of spheres of a fixed radius centred on that curve. (Other examples can be found in [11], chapter II and [4], chapter 5). In what follows we shall be entirely concerned with the local structure of such envelopes. 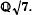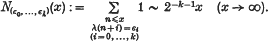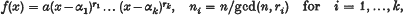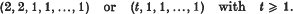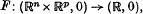So essentially we have a smooth map germ with 0 a regular value of the restriction of 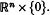F to . For 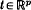near 0 we have 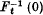a smooth hypersurface near 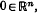, where 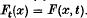. The envelope of this family of hypersurfaces is obtained by eliminating t from the equations . 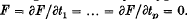Moreover, it can be identified with the discriminant of 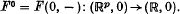F viewed as an unfolding, by the x variables, of the function germ . This observation, together with standard results on versal unfoldings of functions, allows one to determine the local structure of many ‘generic’ geometric envelopes. See [2] for details.

In this paper we have two objectives. The first is to investigate the restriction of a metaplectic cover to an arbitrary torus in GL2. This will be explained at greater length below, and the main results are Theorems 1 and 2. The second is an application of the same ideas to introduce the arithmetic function P, which has already appeared in a special case in [9], and to prove the fundamental property given by Theorem 3. These theorems will be proved in §§ 2 and 3. In §§ 4 and 5 we remark on the appearence of the function P in the formula of Loxton and Matthews [5], [6] for the biquadratic Gauss sum and discuss the structure of this formula.

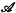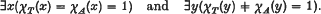
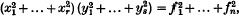
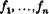A family of sets is said to possess property B if there is a set T such that A ∪ T ╪ ø and yet A ⊈ T for all sets A in . These two requirements may be restated in terms of the characteristic functions of the sets in as follows:

Hurwitz [6] posed in 1898 the problem of determining, for given integers r and s, the least integer n, denoted by r s, for which there exists an [r, s, n] formula, namely a sums of squares formula of the type

where are bilinear forms with real coefficients in 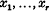and 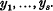. Such an 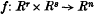[r, s, n] formula is equivalent to a normed bilinear map satisfying 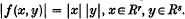. We shall, therefore, speak of sums of squares formulae and normed bilinear maps interchangeably.