One page in Ramanujan's lost notebook is devoted to claims about a certain integral with two parameters. One claim gives an inversion formula for the integral that is similar to the transformation formula for theta functions. Other claims are remindful of Gauss sums. In this paper we prove all the claims made by Ramanujan about this integral.

Which smooth compact 4-manifolds admit an Einstein metric with non-negative Einstein constant? A complete answer is provided in the special case of 4-manifolds that also happen to admit either a complex structure or a symplectic structure.

We improve the current upper and lower bounds for the normal order of the Erdős–Hooley Δ–functionobtaining, for almost all integers n, the inequalitieswhere the exponent γ := (log 2)/log((1−1/log 27)/(1 − 1/log 3)) ≈ 0.33827 is conjectured to be optimal.

Let 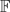be a field and 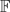[x, y] the ring of polynomials in two variables over 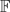. Let f ∈ 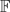[x, y] and consider the residue class ring R := 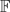[x, y]/f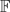[x, y]. Our first aim is to study digit representations in R, i.e., we ask for which f each element of R admits a digit representation of the form d0 + d1x + ⋅ ⋅ ⋅ + dℓxℓ with digits di ∈ 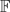[y] satisfying degy(di) < degy(f). These digit systems are motivated by the well-known notion of canonical number systems. Next we enlarge the ring in order to allow representations including negative powers of the “base” x. In particular, we define and characterize digit representations for the ring S := 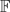((x−1, y−1))/f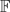((x−1, y−1)) and give easy to handle criteria for finiteness and periodicity of such representations. Finally, we attach fundamental domains to our digit systems. The fundamental domain of a digit system is the set of all elements having only negative powers of x in their “x-ary” representation. The translates of the fundamental domain induce a tiling of S. Interestingly, the fundamental domains of our digit systems turn out to be unions of boxes. If we choose 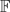=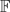q to be a finite field, these unions become finite.

We prove that, for any irrational number α, there are infinitely many primes p such that ∥αp∥ < p−1/3+ε. Here ∥y∥ denotes the distance from y to the nearest integer. The proof uses Harman's sieve method with arithmetical information coming from bounds for averages of Kloosterman sums.

We transfer the results of Dyer, Formanek and Kassabov on the automorphism towers of finitely generated free nilpotent groups to infinitely generated free nilpotent groups. We prove that the automorphism groups of infinitely generated free nilpotent groups are complete. By combining the results of Dyer, Formanek and Kassabov with the results in this paper, one gets that the automorphism tower of any free nilpotent group terminates after finitely many steps.

In 2000, L. Héthelyi and B. Külshammer proved that if p is a prime number dividing the order of a finite solvable group G, then G has at least conjugacy classes. In this paper we show that if p is large, the result remains true for arbitrary finite groups.

We carry out an Eisenstein prime descent to prove the finiteness of the Mordell-Weil group of the Eisenstein quotients of J1(p) for certain values of p that are relevant to torsion in elliptic curves over cubic fields. We then use this to recover some results of Parent. Our methods suggest a possible generalization of Ogg's conjecture for torsion in elliptic curves over number fields.

Given a system of diagonal forms over ℚp, we ask how many variables are required to guarantee that the system has a nontrivial zero. We show that if the prime p satisfies p > (largest degree) − (smallest degree) + 1, then there is a bound on the sufficient number of variables which is a polynomial in the degrees of the forms.

We investigate the zeros of q-Bessel functions of the second and third types as well as those of the associated finite q-Hankel transforms. We derive asymptotic relations of the zeros of the q-Bessel functions by comparison with zeros of the theta function. The asymptotics of q-Bessel functions are also given. Zeros of finite q-Hankel transforms of q-summable functions are shown to be real and simple except for a finite number of possible non real zeros. Sufficient conditions are given to guarantee that all zeros are real. We give some applications concerning zeros of combinations of q-Bessel functions.

We reformulate the construction of Kontsevich's completion and use Lawson homology to define many new motivic invariants. We show that the dimensions of subspaces generated by algebraic cycles of the cohomology groups of two K-equivalent varieties are the same, which implies that several conjectures of algebraic cycles are K-statements. We define stringy functions which enable us to ask stringy Grothendieck standard conjecture and stringy Hodge conjecture. We prove a projective bundle theorem in morphic cohomology for trivial bundles over any normal quasi-projective varieties.

Motivated by research on hyperfinite equivalence relations we define a coloring property for countable groups. We prove that every countable group has the coloring property. This implies a compactness theorem for closed complete sections of the free part of the shift action of G on 2G. Our theorems generalize known results about .

We prove a decomposition theorem similar to the well-known result of Voiculescu's: namely that completely positive maps A → (B)/B factor through a given homomorphism ι: A →(B)/B when the homomorphism ι has a certain infiniteness property.

The algebra B is only assumed to be separable and nonunital; in particular, it is not assumed to be stable. The C*-algebra A is assumed to be separable, unital and nuclear.

The combined conjecture of Lang-Bogomolov for tori gives an accurate description of the set of those points x of a given subvariety of , that with respect to the height are “very close” to a given subgroup Γ of finite rank of . Thanks to work of Laurent, Poonen and Bogomolov, this conjecture has been proved in a more precise form.

In this paper we prove, for certain special classes of varieties , effective versions of the Lang-Bogomolov conjecture, giving explicit upper bounds for the heights and degrees of the points x under consideration. The main feature of our results is that the points we consider do not have to lie in a prescribed number field. Our main tools are Baker-type logarithmic forms estimates and Bogomolov-type estimates for the number of points on the variety with very small height.

We study locally constant coefficients. We first study the theory of homotopy Kan extensions with locally constant coefficients in model categories, and explain how it characterizes the homotopy theory of small categories. We explain how to interpret this in terms of left Bousfield localization of categories of diagrams with values in a combinatorial model category. Finally, we explain how the theory of homotopy Kan extensions in derivators can be used to understand locally constant functors.

We present a constructive proof of Gelfand duality for C*-algebras by reducing the problem to Gelfand duality for real C*-algebras.

We explain how any cofibrantly generated weak factorisation system on a category may be equipped with a universally and canonically determined choice of cofibrant replacement. We then apply this to the theory of weak ω-categories, showing that the universal and canonical cofibrant replacement of the operad for strict ω-categories is precisely Leinster's operad for weak ω-categories.

In this paper, we apply Stein's method for distributional approximations to prove a quantitative form of the Erdös–Kac Theorem. We obtain our best bound on the rate of convergence, on the order of log log log n (log log n)−1/2, by making an intermediate Poisson approximation; we believe that this approach is simpler and more probabilistic than others, and we also obtain an explicit numerical value for the constant implicit in the bound. Different ways of applying Stein's method to prove the Erdös–Kac Theorem are discussed, including a Normal approximation argument via exchangeable pairs, where the suitability of a Poisson approximation naturally suggests itself.

Working in a semi-abelian context, we use Janelidze's theory of generalised satellites to study universal properties of the Everaert long exact homology sequence. This results in a new definition of homology which does not depend on the existence of projective objects. We explore the relations with other notions of homology, and thus prove a version of the higher Hopf formulae. We also work out some examples.

Let FN be a free group of finite rank N ≥ 2, and let T be an ℝ-tree with a very small, minimal action of FN with dense orbits. For any basis of FN there exists a heart ⊂ (= the metric completion of T) which is a compact subtree that has the property that the dynamical system of partial isometries ai : , for each ai ∈ , defines a tree which contains an isometric copy of T as minimal subtree.