Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-30T20:20:18.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Number systems and tilings over Laurent series

Published online by Cambridge University Press:  01 July 2009

TOBIAS BECK ,
HORST BRUNOTTE ,
KLAUS SCHEICHER  and
JÖRG M. THUSWALDNER
TOBIAS BECK
Affiliation:
Johann Radon Institute for Computational and Applied Mathematics, Austrian Academy of Sciences, Altenbergerstrasse 69, A-4040 Linz, Austria. e-mail: [email protected]
HORST BRUNOTTE
Affiliation:
Haus-Endt-Strasse 88, D-40593 Düsseldorf, Germany. e-mail: [email protected]
KLAUS SCHEICHER
Affiliation:
Institut für Mathematik, Universität für Bodenkultur, Gregor Mendel Strasse 33, A-1180 Wien, Austria. e-mail: [email protected]
JÖRG M. THUSWALDNER
Affiliation:
Institut für Mathematik und Informationstechnologie, Abteilung für Mathematik und Statistik, Montanuniversität Leoben, Franz Josef Strasse 18, A-8700 Leoben, Austria. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 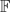be a field and 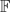[x, y] the ring of polynomials in two variables over 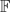. Let f ∈ 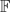[x, y] and consider the residue class ring R := 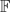[x, y]/f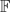[x, y]. Our first aim is to study digit representations in R, i.e., we ask for which f each element of R admits a digit representation of the form d0 + d1x + ⋅ ⋅ ⋅ + dℓxℓ with digits di ∈ 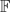[y] satisfying degy(di) < degy(f). These digit systems are motivated by the well-known notion of canonical number systems. Next we enlarge the ring in order to allow representations including negative powers of the “base” x. In particular, we define and characterize digit representations for the ring S := 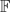((x−1, y−1))/f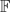((x−1, y−1)) and give easy to handle criteria for finiteness and periodicity of such representations. Finally, we attach fundamental domains to our digit systems. The fundamental domain of a digit system is the set of all elements having only negative powers of x in their “x-ary” representation. The translates of the fundamental domain induce a tiling of S. Interestingly, the fundamental domains of our digit systems turn out to be unions of boxes. If we choose 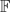=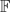q to be a finite field, these unions become finite.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 147 , Issue 1 , July 2009 , pp. 9 - 29
Copyright
Copyright © Cambridge Philosophical Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Akiyama, S., Borbély, T., Brunotte, H., Pethő, A. and Thuswaldner, J. M.Generalized radix representations and dynamical systems. I. Acta Math. Hungar. 108 (3) (2005), 207–238.CrossRefGoogle Scholar
[2]Akiyama, S. and Thuswaldner, J. M.The topological structure of fractal tilings generated by quadratic number systems. Comput. Math. Appl. 49 (9–10) (2005), 1439–1485.CrossRefGoogle Scholar
[3]Allouche, J.-P., Cateland, E., Gilbert, W. J., Peitgen, H.-O., Shallit, J. O. and Skordev, G.Automatic maps in exotic numeration systems. Theory Comput. Syst. (Math. Systems Theory) 30 (1997), 285–331.CrossRefGoogle Scholar
[4]Barat, G., Berthé, V., Liardet, P. and Thuswaldner, J.Dynamical directions in numeration. Annal. Inst. Fourier 56 (2006), 1987–2092.CrossRefGoogle Scholar
[5]Fernau, H.Infinite iterated function systems. Math. Nachr. 170 (1994), 79–91.CrossRefGoogle Scholar
[6]Gilbert, W. J.Radix representations of quadratic fields. J. Math. Anal. Appl. 83 (1981), 264–274.CrossRefGoogle Scholar
[7]Grossman, E. H.Number bases in quadratic fields. Stud. Sci. Math. Hung. 20 (1985), 55–58.Google Scholar
[8]Hbaib, M. and Mkaouar, M.Sur le bêta-développement de 1 dans le corps des séries formelles. Int. J. Number Theory 2 (3) (2006), 365–378.CrossRefGoogle Scholar
[9]Hutchinson, J. E.Fractals and self-similarity. Indiana Univ. Math. J. 30 (1981), 713–747.CrossRefGoogle Scholar
[10]Kátai, I. and Környei, I.On number systems in algebraic number fields. Publ. Math. Debrecen 41 (3–4) (1992), 289–294.CrossRefGoogle Scholar
[11]Kátai, I. and Kovács, B.Kanonische Zahlensysteme in der Theorie der Quadratischen Zahlen. Acta Sci. Math. (Szeged) 42 (1980), 99–107.Google Scholar
[12]Kátai, I. and Kovács, B.Canonical number systems in imaginary quadratic fields. Acta Math. Hungar. 37 (1981), 159–164.CrossRefGoogle Scholar
[13]Kátai, I. and Szabó, J.Canonical number systems for complex integers. Acta Sci. Math. (Szeged) 37 (1975), 255–260.Google Scholar
[14]Knuth, D. E. The Art of Computer Programming, Vol 2: Seminumerical Algorithms (Addison Wesley, 3rd edition, 1998).Google Scholar
[15]Pethő, A. On a polynomial transformation and its application to the construction of a public key cryptosystem. In Computational Number Theory (Debrecen, 1989), (de Gruyter, 1991) pages 31–43.Google Scholar
[16]Scheicher, K.β-expansions in algebraic function fields over finite fields. Finite Fields Appl. 13 (2007), 394–410.CrossRefGoogle Scholar
[17]Scheicher, K. and Thuswaldner, J. M.Canonical number systems, counting automata and fractals. Math. Proc. Camb. Phil. Soc. 133 (1) (2002), 163–182.CrossRefGoogle Scholar
[18]Scheicher, K. and Thuswaldner, J. M.Digit systems in polynomial rings over finite fields. Finite Fields Appl. 9 (3) (2003), 322–333.CrossRefGoogle Scholar