Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
BRESSAUD, XAVIER
and
JULLIAN, YANN
2012.
INTERVAL EXCHANGE TRANSFORMATION EXTENSION OF A SUBSTITUTION DYNAMICAL SYSTEM.
Confluentes Mathematici,
Vol. 04,
Issue. 04,
p.
1250005.
Coulbois, Thierry
and
Hilion, Arnaud
2012.
Botany of irreducible automorphisms of free groups.
Pacific Journal of Mathematics,
Vol. 256,
Issue. 2,
p.
291.
Jullian, Yann
2013.
An algorithm to identify automorphisms which arise from self-induced interval exchange transformations.
Mathematische Zeitschrift,
Vol. 274,
Issue. 1-2,
p.
33.
Francaviglia, Stefano
and
Martino, Armando
2015.
Stretching factors, metrics and train tracks for free products.
Illinois Journal of Mathematics,
Vol. 59,
Issue. 4,
Bestvina, Mladen
and
Reynolds, Patrick
2015.
The boundary of the complex of free factors.
Duke Mathematical Journal,
Vol. 164,
Issue. 11,
COULBOIS, THIERRY
and
HILION, ARNAUD
2016.
Ergodic currents dual to a real tree.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 3,
p.
745.
Guirardel, Vincent
and
Horbez, Camille
2019.
Algebraic laminations for free products and arational trees.
Algebraic & Geometric Topology,
Vol. 19,
Issue. 5,
p.
2283.
Algom-Kfir, Yael
Hilion, Arnaud
and
Stark, Emily
2021.
The visual boundary of hyperbolic free-by-cyclic groups.
Israel Journal of Mathematics,
Vol. 244,
Issue. 2,
p.
501.


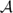 of
of 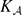 ⊂
⊂ 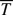 (= the metric completion of
(= the metric completion of 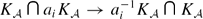 , for each
, for each 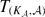 which contains an isometric copy of
which contains an isometric copy of 