We prove that

thus dealing with open problems concerning divisors of binomial coefficients.

We present a new way of forming a grothendieck group with respect to exact sequences. A ‘defect’ is attached to each non-split sequence and the relation that would normally be derived from a collection of exact sequences is only effective if the (signed) sum of the corresponding defects is zero. The theory of the localization exact sequence and, in particular, of the relative group in this sequence is developed. The (‘locally free’) class group of a module category with exactness defect is defined and an idèlic formula for this is given. The role of torsion and of torsion-free modules is investigated. One aim of the work is to enhance the locally trivial, ‘class group’, invariants obtainable for a module while keeping to a minimum the local obstructions to the definition of such invariants.

In this paper we calculate part of the integral cohomology ring of the sporadic simple group J4; this group has order 221.33.5.7. 113.23.29.31.37.43. More precisely, we obtain all of the cohomology ring except for the 2-primary part. As the cohomology has already been written down [9] at the primes which divide the group order only once, we concentrate here on the primes 3 and 11. In both of these cases the Sylow p-subgroups are extraspecial of order p3 and exponent p. We use the method which identifies the p-primary cohomology with the ring of stable classes in the cohomology of a Sylow p-subgroup. The stable classes are all invariant under the action of the Sylow p-normalizer; and some time is spent finding invariant classes in the cohomology ring of , the extraspecial group. Section 2 studies the prime 11: the invariant classes are the stable classes, because the Sylow 11-subgroups have the Trivial Intersection (T.I.) property. In Section 3 we study the prime 3, and see that all conditions for invariant classes to be stable reduce to one condition.

The Whitney quasi-rank generating function, which generalizes the Whitney rank generating function (or Tutte polynomial) of a graph, is introduced. It is found to include as special cases the weight enumerator of a (not necessarily linear) code, the percolation probability of an arbitrary clutter and a natural generalization of the chromatic polynomial. The crucial construction, essentially equivalent to one of Kung, is a means of associating, to any function, a rank-like function with suitable properties. Some of these properties, including connections with the Hadamard transform, are discussed.

Consider the finite set Xn = {1,2, …,n} ordered in the standard way. Let Tn denote the full transformation semigroup on Xn, that is, the semigroup of all mappings α: Xn→Xn under composition. We shall call α order-preserving if i ≤ j implies iα ≤ jα for i,j∈Xn, and α is decreasing if iα ≤ i for all i∈Xn. This paper investigates combinatorial properties of the semigroup O of all order-preserving mappings on Xn, and of its subsemigroup C which consists of all decreasing and order-preserving mappings.

The genesis of this paper lies in theoretical questions in kinematics where a central role is played by naturally occurring families of rigid motions of 3-space. The resulting trajectories are parametrized families of space curves, and it is important to understand the generic singularities they can exhibit. For practical purposes one seeks to classify germs of space curves of fairly small Ae-codimension. It is however little harder to list the A-simple germs, which includes all germs of Ae-codimension ≤11: that then is the principal objective of this paper.

Let p be any prime. It is well known that the modp Dyer-Lashof algebra acts trivially on the mod p homology of an Eilenberg-MacLane space. The main result of this paper is a converse of this fact. Specifically, it is shown that any connected infinite loop space with trivial action of the mod p Dyer-Lashof algebra is (localized at p) homotopy equivalent to a product of Eilenberg-MacLane spaces. It is then shown that this equivalence does not necessarily respect the infinite loop structures involved.

In [11], Partington proved that if λ is a Banach sequence space with a monotone basis having the Banach-Saks property, and (Xn) is a sequence of Banach spaces each having the Banach-Saks property, then the vector sequence space ΣλXn has this same property. In addition, Partington gave an example showing that if λ and each Xn, have the weak Banach-Saks property, then ΣλXn need not have the weak Banach-Saks property.

The main result in this note is as follows. Let E be a Fréchet Montel space which belongs to the large class of decomposable (FG)-spaces introduced by Bonet, Díaz, Taskinen and let F be a Fréchet Montel (resp. distinguished) space. Then the projective tensor product is Montel (resp. distinguished). We also give examples of Montel decomposable (FG)-spaces without an unconditional basis.

The Poincaré disc model

of two-dimensional hyperbolic space supports a metric ρ derived from the differential

Geodesics for the metric ρ are arcs of circles orthogonal to the unit circle S, and straight lines through the origin.

Given any domain Ω in ℝN we consider spaces X = X(Ω),Y = Y(Ω) which are Banach function spaces in the sense of Luxemburg [12]. From these we form what we call the abstract Sobolev space W(X, Y), which is denned to be the linear space of all ƒ ∈ X such that for i = 1, …, N, the distributional derivative ∂ƒ/∂xi belongs to Y; equipped with the norm

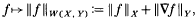
W(X, Y) is a Banach space. The closure of (Ω) in W(X, Y) is denoted by W0(X, Y). Let w to bea weight function on Ω, that is, a measurable function which is positive and finite almost everywhere on Ω. We say that [w, X, Y] supports the (weighted) Poincaré inequality if there is a positive constant K such that for all u ∈ W(X, Y),

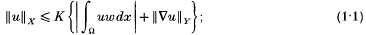
analogously, [X, Y] is said to support the Friedrichs inequality if there is a positive constant K such that for all u ∈ W0(X, Y),

In Baxter and Williams [1] we began a study of Abel averages,

as opposed to the oft-studied Cesàro averages In Baxter and Williams [2], hereinafter referred to as [BW2], we studied the large-deviation behaviour of these averages. In the case where X is an irreducible Markov chain on a finite state-space S = {1,…, n}, we observed that

and

where π is the invariant distribution of X. We noted that

where v is an n-vector, δ(v):= sup{Re(z): z ∈ spect(Q+ V)}, and where spect(·) denotes spectrum (here the set of eigenvalues), Q is the Q-matrix of X, and V denotes the diagonal matrix diag (vi). It is also true that the large-deviation property holds for Ct with rate function I denned on M = {(xt)i ∈ S: xi ≥ 0, Σixi = 1}.

In this paper we obtain criteria for a reflecting Brownian motion in the first orthant of the plane to reach an arbitrary open neighbourhood of the origin in finite time, or in finite mean time. The reflecting Brownian motion (RBM) is assumed to have a constant non-zero drift, and a constant non-singular covariance, and the directions of reflection on the two sides of are constant along each side, but not necessarily normal. We explain why the criteria we find are to be expected.

Recently Kauffman[2, 3] has classified the (strongly) spin-preserving solutions of the Yang—Baxter equation, and in particular discussed two solutions. One of these can be used to obtain the Jones polynomial, while the other (with care) leads to the Alexander polynomial. In this paper we shall complete this analysis, and shall describe all strongly spin-preserving invertible solutions of the Yang-Baxter equation which lead to link invariants. Having done this, we investigate what sort of link invariants can be obtained from these solutions. It turns out that these invariants are precisely those which have been described in Hennings [l].

The problem of periodicity of solutions of the generalized Liénard equation

has attracted much attention. Many efforts have been made to give sufficient conditions to guarantee the existence and the uniqueness of periodic solutions (limit cycles) of (1·1). There are also some papers on the number of limit cycles of (1·1) (see, for example, [3, 5, 6, 13]). However, there are only a few results on non-existence of periodic solutions of (1·1).

In this paper, we establish the generalized eigenfunction expansions for wave propagation in inhomogeneous, penetrable media in ℝn(n ≥ 2) with an unbounded interface. We then use them together with the method of stationary phase to prove the existence of the wave operators and to obtain the representations of the wave operators in terms of the generalized Fourier transforms.