Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T14:00:54.242Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetry characterizations of certain distributions. 3. Discounted additive functional and large deviations for a general finite-state Markov chain

Published online by Cambridge University Press:  24 October 2008

Martin Baxter
Martin Baxter
Affiliation:
Statistical Laboratory, University of Cambridge., Cambridge CB2 1SB
Get access Rights & Permissions [Opens in a new window]

Extract

In Baxter and Williams [1] we began a study of Abel averages,

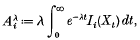
as opposed to the oft-studied Cesàro averages 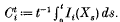In Baxter and Williams [2], hereinafter referred to as [BW2], we studied the large-deviation behaviour of these averages. In the case where X is an irreducible Markov chain on a finite state-space S = {1,…, n}, we observed that

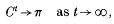
and

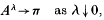
where π is the invariant distribution of X. We noted that

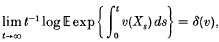
where v is an n-vector, δ(v):= sup{Re(z): z ∈ spect(Q+ V)}, and where spect(·) denotes spectrum (here the set of eigenvalues), Q is the Q-matrix of X, and V denotes the diagonal matrix diag (vi). It is also true that the large-deviation property holds for Ct with rate function I denned on M = {(xt)i ∈ S: xi ≥ 0, Σixi = 1}.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 113 , Issue 2 , March 1993 , pp. 381 - 386
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baxter, M. W. and Williams, D.. Symmetry characterizations of certain distributions, 1. Math. Proc. Cambridge Philos. Soc. 111 (1992), 387–397.CrossRefGoogle Scholar
[2]Baxter, M. W. and Williams, D.. Symmetry characterizations of certain distributions, 2: Discounted additive functionals and large deviations. Math. Proc. Cambridge Philos. Soc. 112 (1992), 599–611.CrossRefGoogle Scholar
[3]Ellis, R. S.. Large deviations for a general class of random vectors. Ann. Probab. 12 (1984), 1–12.CrossRefGoogle Scholar
[4]Kato, T.. A Short Introduction to Perturbation Theory for Linear Operators (Springer-Verlag, 1982).CrossRefGoogle Scholar
[5]Seneta, E.. Non-negative Matrices, an Introduction to Theory and Applications (Allen and Unwin, 1973).Google Scholar