Research Article
On generic structures with a strong amalgamation property
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 721-733
-
- Article
- Export citation
The model completion of the theory of modules over finitely generated commutative algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 734-750
-
- Article
- Export citation
The self-iterability of L[E]
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 751-779
-
- Article
- Export citation
Equivalence of consequence relations: an order-theoretic and categorical perspective
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 780-810
-
- Article
- Export citation
Strongly representable atom structures of cylindric algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 811-828
-
- Article
- Export citation
Approximate counting by hashing in bounded arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 829-860
-
- Article
- Export citation
Lawvere–Tierney sheaves in Algebraic Set Theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 861-890
-
- Article
- Export citation
Cohomology of groups in o-minimal structures: acyclicity of the infinitesimal subgroup
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 891-900
-
- Article
- Export citation
Saturation and Σ2-transfer for ERNA
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 901-913
-
- Article
- Export citation
The amalgamation spectrum
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 914-928
-
- Article
- Export citation
A geometric zero-one law
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 929-938
-
- Article
- Export citation
The complexity of learning SUBSEQ(A)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 939-975
-
- Article
- Export citation
Kreisel's Conjecture with minimality principle
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 976-988
-
- Article
- Export citation
Bounding non-GL2 and R.E.A.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 989-1000
-
- Article
- Export citation
The existence of a near-unanimity term in a finite algebra is decidable
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1001-1014
-
- Article
- Export citation
Combined Maximality Principles up to large cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1015-1046
-
- Article
- Export citation
Intrinsic bounds on complexity and definability at limit levels
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1047-1060
-
- Article
- Export citation
Countable Fréchet Boolean groups: An independence result
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1061-1068
-
- Article
- Export citation
The number of normal measures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1069-1080
-
- Article
- Export citation
Front matter
JSL volume 74 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation

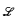 be a finite relational language and
be a finite relational language and 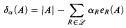
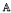 , where
, where 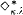 holds true, and if in addition
holds true, and if in addition 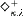 holds true.
holds true.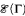 , and prove, for infinite Γ, that
, and prove, for infinite Γ, that 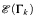 is strongly representable (each
is strongly representable (each 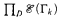 is not.
is not.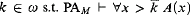 . The results imply that PA
. The results imply that PA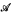 that is
that is 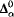 categorical, but not relatively
categorical, but not relatively 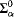 Scott family). We also show that for every computable limit ordinal
Scott family). We also show that for every computable limit ordinal