Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Aguilera, J. P.
Pakhomov, F.
and
Weiermann, A.
2023.
Modern perspectives in Proof Theory.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 381,
Issue. 2248,


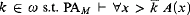 . The results imply that PA
. The results imply that PA