Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Busche, Daniel
and
Schindler, Ralf
2009.
The strength of choiceless patterns of singular and weakly compact cardinals.
Annals of Pure and Applied Logic,
Vol. 159,
Issue. 1-2,
p.
198.
Schlicht, Philipp
2014.
Thin equivalence relations and inner models.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 10,
p.
1577.
Sargsyan, Grigor
2014.
Nontame mouse from the failure of square at a singular strong limit cardinal.
Journal of Mathematical Logic,
Vol. 14,
Issue. 01,
p.
1450003.
Ikegami, Daisuke
and
Väänänen, Jouko
2015.
Boolean-Valued Second-Order Logic.
Notre Dame Journal of Formal Logic,
Vol. 56,
Issue. 1,
Zhu, Yizheng
2015.
Realizing an AD+ model as a derived model of a premouse.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 12,
p.
1275.
Daghighi, Ali Sadegh
and
Pourmahdian, Massoud
2016.
The definable tree property for successors of cardinals.
Archive for Mathematical Logic,
Vol. 55,
Issue. 5-6,
p.
785.
Trang, Nam
2016.
PFA and guessing models.
Israel Journal of Mathematics,
Vol. 215,
Issue. 2,
p.
607.
Barton, Neil
Caicedo, Andrés Eduardo
Fuchs, Gunter
Hamkins, Joel David
Reitz, Jonas
and
Schindler, Ralf
2020.
Inner-Model Reflection Principles.
Studia Logica,
Vol. 108,
Issue. 3,
p.
573.
Müller, Sandra
Schindler, Ralf
and
Woodin, W. Hugh
2020.
Mice with finitely many Woodin cardinals from optimal determinacy hypotheses.
Journal of Mathematical Logic,
Vol. 20,
Issue. Supp01,
p.
1950013.
Schlutzenberg, Farmer
2021.
Iterability for (transfinite) stacks.
Journal of Mathematical Logic,
Vol. 21,
Issue. 02,
p.
2150008.
SARGSYAN, GRIGOR
2023.
NEGATIVE RESULTS ON PRECIPITOUS IDEALS ON .
The Journal of Symbolic Logic,
Vol. 88,
Issue. 2,
p.
490.
Schlutzenberg, Farmer
2023.
The definability of E in self-iterable mice.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 2,
p.
103208.
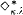 holds true, and if in addition λ is regular, then
holds true, and if in addition λ is regular, then 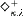 holds true.
holds true.

