Article contents
Strongly representable atom structures of cylindric algebras
Published online by Cambridge University Press: 12 March 2014
Abstract
A cylindric algebra atom structure is said to be strongly representable if all atomic cylindric algebras with that atom structure are representable. This is equivalent to saying that the full complex algebra of the atom structure is a representable cylindric algebra. We show that for any finite n ≥ 3, the class of all strongly representable n-dimensional cylindric algebra atom structures is not closed under ultraproducts and is therefore not elementary.
Our proof is based on the following construction. From an arbitrary undirected, loop-free graph Γ, we construct an n-dimensional atom structure 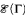 , and prove, for infinite Γ, that
, and prove, for infinite Γ, that 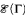 is a strongly representable cylindric algebra atom structure if and only if the chromatic number of Γ is infinite. A construction of Erdős shows that there are graphs Γk(k < ω) with infinite chromatic number, but having a non-principal ultraproduct ΠDΓk whose chromatic number is just two. It follows that
is a strongly representable cylindric algebra atom structure if and only if the chromatic number of Γ is infinite. A construction of Erdős shows that there are graphs Γk(k < ω) with infinite chromatic number, but having a non-principal ultraproduct ΠDΓk whose chromatic number is just two. It follows that 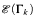 is strongly representable (each k < ω) but
is strongly representable (each k < ω) but 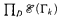 is not.
is not.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2009
References
REFERENCES
- 7
- Cited by


