Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T19:50:33.505Z Has data issue: false hasContentIssue false
  • English
  • Français

Collisional alpha transport in a weakly non-quasisymmetric stellarator magnetic field

Part of: Focus on Fusion

Published online by Cambridge University Press:  02 May 2019

Peter J. Catto
Peter J. Catto*
Affiliation:
Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Alpha particle confinement is a serious concern in stellarators and provides strong motivation for optimizing magnetic field configurations. In addition to the collisionless confinement of trapped alphas in stellarators, excessive collisional transport of the trapped alpha particles must be avoided while they tangentially drift due to the magnetic gradient (the 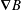$\unicode[STIX]{x1D735}B$ drift). The combination of pitch angle scatter off the background ions and the 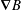$\unicode[STIX]{x1D735}B$ drift gives rise to two narrow boundary layers in the trapped region. The first is at the trapped–passing boundary and enables the finite trapped response to be matched to the vanishing passing response of the alphas. The second layer is a region that encompasses the somewhat more deeply trapped alphas with vanishing tangential 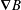$\unicode[STIX]{x1D735}B$ drift. Away from (and between) these boundary layers, collisions are ineffective and the alpha 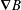$\unicode[STIX]{x1D735}B$ drift simply balances the small radial drift of the trapped alphas. As this balance does not vanish as the trapped–passing boundary is approached, the first collisional boundary layer is necessary and gives rise to 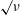$\surd \unicode[STIX]{x1D708}$ transport, with $\unicode[STIX]{x1D708}$ the collision frequency. The vanishing of the tangential drift results in a separate, somewhat wider boundary layer, and significantly stronger superbanana plateau transport that is independent of collisionality. The constraint imposed by the need to avoid significant energy depletion loss in the slowing down tail distribution function sets the allowed departure of a stellarator from an optimal quasisymmetric configuration.

Keywords

fusion plasmaplasma confinementplasma flows
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 2 , April 2019 , 905850213
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beidler, C. D., Allmaier, K., Isaev, M. Y., Kasilov, S. V., Kernbichler, W., Leitold, G. O., Maaßberg, H., Mikkelsen, D. R., Murakami, S., Schmidt, M. et al. 2011 Benchmarking of the mono-energetic transport coefficients – results from the International Collaboration on Neoclassical Transport in Stellarators (ICNTS). Nucl. Fusion 51, 076001, 28 pp.Google Scholar
Beidler, C. D. & D’haeseleer, W. D. 1995 A general solution of the ripple-averaged kinetic equation (GSRAKE). Plasma Phys. Control. Fusion 37, 463–490.Google Scholar
Boozer, A. H. 1981 Plasma equilibrium with rational magnetic surfaces. Phys. Fluids 24, 1999–2003.Google Scholar
Boozer, A. H. 1983 Transport and isomorphic equilibria. Phys. Fluids 26, 496–499.Google Scholar
Boozer, A. H. 1995 Quasi-helical symmetry in stellarators. Plasma Phys. Control. Fusion 37, A103–A117.Google Scholar
Calvo, I., Parra, F. I., Velasco, J. L. & Alonso, J. A. 2017 The effect of tangential drifts on neoclassical transport in stellarators close to omnigeneity. Plasma Phys. Control. Fusion 59, 055014, 19pp.Google Scholar
Catto, P. J. 2018 Ripple modifications to alpha transport in tokamaks. J. Plasma Phys. 84, 905840508, 39pp.Google Scholar
Catto, P. J. 2019 Collisional alpha transport in a weakly rippled magnetic field. J. Plasma Phys. 85, 905850203, 16pp.Google Scholar
Garren, D. A. & Boozer, A. H. 1991a Magnetic field strength of toroidal plasma equilibria. Phys. Fluids B 3, 2805–2821.Google Scholar
Garren, D. A. & Boozer, A. H. 1991b Existence of quasihelically symmetric stellarators. Phys. Fluids B 3, 2822–2834.Google Scholar
Gates, D. A., Boozer, A. H., Brown, T., Breslau, J., Curreli, D., Landreman, M., Lazerson, S. A., Lore, J., Mynick, H., Neilson, G. H. et al. 2017 Recent advances in stellarator optimization. Nucl. Fusion 57, 126064, 9pp.Google Scholar
Galeev, A. A. & Sagdeev, R. Z. 1970 Paradoxes of classical diffusion of plasma in toroidal magnetic traps. Sov. Phys. Uspekhi 12, 810–811.Google Scholar
Galeev, A. A. & Sagdeev, R. Z. 1979 Theory of neoclassical diffusion. In Reviews of Plasma Physics (ed. Leontovich, M. A.), vol. 7, pp. 257–343. Consultants Bureau.Google Scholar
Galeev, A. A., Sagdeev, R. Z., Furth, H. P. & Rosenbluth, M. N. 1969 Plasma diffusion in a toroidal stellarator. Phys. Rev. Lett. 22, 511–514.Google Scholar
Henneberg, S. A., Drevlak, M., Nührenberg, C., Beidler, C. D., Turkin, Y., Loizu, J. & Helander, P. 2019 Properties of a new quasi-axisymmetric configuation. Nucl. Fusion 59, 026014, 11 pp.Google Scholar
Ho, D. D-M. & Kulsrud, R. M. 1987 Neoclassical transport in stellarators. Phys. Fluids 30, 442–461.Google Scholar
Landreman, M. & Catto, P. J. 2011 Effects of the radial electric field in a quasisymmetric stellarator. Plasma Phys. Control. Fusion 53, 015004, 28pp.Google Scholar
Landreman, M. & Sengupta, W. 2018 Direct construction of optimized stellarator shapes. Part 1. Theory in cylindrical coordinates. J. Plasma Phys. 84, 905840616, 22pp.Google Scholar
Landreman, M., Sengupta, W. & Plunk, G. 2019 Direct construction of optimized stellarator shapes. Part 2. Numerical quasisymmetric solutions. J. Plasma Phys. 85, 905850103, 22pp.Google Scholar
Mynick, H. E. 1983 Effect of collisionless detrapping on nonaxisymmetric transport in a stellarator with radial electric field. Phys. Fluids 26, 2609–2615.Google Scholar
Nührenberg, J. & Zille, R. 1988 Quasi-helically symmetric toroidal stellarators. Phys. Lett. A 129, 113–117.Google Scholar
Pytte, A. & Boozer, A. H. 1981 Neoclassical transport in helically symmetric plasmas. Phys. Fluids 24, 88–92.Google Scholar
Shaing, K. C. 2015 Superbanana and superbanana plateau transport in finite aspect ratio tokamaks with broken symmetry. J. Plasma Phys. 81, 905810203, 12pp.Google Scholar
Su, C. H. & Oberman, C. 1968 Collisional damping of a plasma echo. Phys. Rev. Lett. 20, 427–429.Google Scholar
White, R. B. 2001 The Theory of Toroidally Confined Plasmas, 2nd edn, pp. 298–302. Imperial College Press.Google Scholar