Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T20:16:45.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Electromagnetic drift instability in a two-dimensional magnetotail – the addition of bouncing electrons

Part of: Focus on Space Plasmas

Published online by Cambridge University Press:  10 April 2019

O. Tsareva ,
G. Fruit ,
P. Louarn  and
A. Tur
O. Tsareva*
Affiliation:
Institut de Recherche en Astrophysique et Planétologie (IRAP), Toulouse, Université de Toulouse, CNRS UMR5277, France
G. Fruit
Affiliation:
Institut de Recherche en Astrophysique et Planétologie (IRAP), Toulouse, Université de Toulouse, CNRS UMR5277, France
P. Louarn
Affiliation:
Institut de Recherche en Astrophysique et Planétologie (IRAP), Toulouse, Université de Toulouse, CNRS UMR5277, France
A. Tur
Affiliation:
Institut de Recherche en Astrophysique et Planétologie (IRAP), Toulouse, Université de Toulouse, CNRS UMR5277, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

To explain the possible destabilization of a two-dimensional magnetic equilibrium such as the near-Earth magnetotail, we developed a kinetic model describing the resonant interaction of electromagnetic fluctuations and bouncing electrons trapped in the magnetic bottle. A small-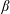$\unicode[STIX]{x1D6FD}$ approximation (i.e., the plasma pressure is lower than the magnetic pressure) is used in agreement with a small field line curvature. The linearized gyro-kinetic Vlasov equation is integrated along the unperturbed particle trajectories, including cyclotron and bounce motions. The dispersion relation for drift-Alfvèn waves is obtained through the plasma quasi-neutrality condition and Ampere’s law for the parallel current. It has been found that for a quasi-dipolar configuration (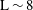$\text{L}\sim 8$ corresponds to the set of the Earth’s magnetic field lines, crossing the Earths magnetic equator at 8 Earth radii), unstable electromagnetic modes may develop in the current sheet with a growth rate of the order of a few tenths of a second provided that the typical scale of density gradient slope responsible for the diamagnetic drift effects is over one Earth radius or less. This instability growth rate is large enough to destabilize the current sheet on time scales of 2–4 minutes as observed during substorm onset.

Keywords

plasma instabilities
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 2 , April 2019 , 905850212
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonsen, T. M. Jr. & Lane, B. 1980 Kinetic equations for low frequency instabilities in inhomogeneous plasmas. Phys. Fluids 23, 1205–1214.Google Scholar
Bellan, P. M. 2008 Fundamentals of Plasma Physics. Cambridge University Press.Google Scholar
Birn, J. & Priest, E. 2007 Reconnexion in Magnetic Fields: Magnetohydrodynamics and Collisionless Theory and Observations. Cambridge University Press.Google Scholar
Cheng, C. Z. 1982 Kinetic theory of collisionless ballooning modes. Phys. Fluids 25, 1020–1026.Google Scholar
Coppi, B. 1964 ‘Inertial’ instabilities in plasmas. Phys. Lett. 11, 226–228.Google Scholar
Coppi, B., Laval, G. & Pellat, R. 1966 Dynamics of the Geomagnetic Tail. Phys. Rev. Lett. 16, 1207–1210.Google Scholar
Fried, B. & Conte, S. 1961 The Plasma Dispersion Function. Academic Press.Google Scholar
Fruit, G., Louarn, P. & Tur, A. 2013 Electrostatic ‘bounce’ instability in a magnetotail configuration. Phys. Plasmas 20 (2), 022113.Google Scholar
Fruit, G., Louarn, P. & Tur, A. 2017 Electrostatic drift instability in a magnetotail configuration: the role of bouncing electrons. Phys. Plasmas 24 (3), 032903.Google Scholar
Galeev, A. A. & Zelenyi, L. M. 1976 Tearing instability in plasma configurations. Zh. Eksp. Teor. Fiz. 70, 2133–2151.Google Scholar
Hasegawa, A. 1975 Plasma Instabilities and Nonlinear Effects, Springer Series on Physics Chemistry Space, vol. 8. Springer.Google Scholar
Hurricane, O. A., Pellat, R. & Coroniti, F. V. 1994 The kinetic response of a stochastic plasma to low frequency perturbations. Geophys. Res. Lett. 21, 253–256.Google Scholar
Kalmoni, N. M. E., Rae, I. J., Watt, C. E. J., Murphy, K. R., Forsyth, C. & Owen, C. J. 2015 Statistical characterization of the growth and spatial scales of the substorm onset arc. J. Geophys. Res. (Space Phys.) 120, 8503–8516.Google Scholar
Kennel, C. F. 1996 Convection and substorms – paradigms of magnetospheric phenomenology. In Convection and Substorms – Paradigms of Magnetospheric Phenomenology, Vol. 2 (ed. Kennel, C. F.), International Series in Astronomy and Astrophysics, vol. 2. Oxford University Press, 432 pages; 35 illus. ISBN13: 978-0-19-508529-7.Google Scholar
Lembege, B. & Pellat, R. 1982 Stability of a thick two-dimensional quasineutral sheet. Phys. Fluids 25, 1995–2004.Google Scholar
Littlejohn, R. G. 1982 Hamiltonian theory of guiding center bounce motion. Phys. Scr. 2A, 119–125.Google Scholar
Lui, A. T. Y. 2016 Cross-field current instability for auroral bead formation in breakup arcs. Geophys. Res. Lett. 43, 6087–6095.Google Scholar
Lui, A. T. Y., Lopez, R. E., Anderson, B. J., Takahashi, K., Zanetti, L. J., McEntire, R. W., Potemra, T. A., Klumpar, D. M., Greene, E. M. & Strangeway, R. 1992 Current disruptions in the near-earth neutral sheet region. J. Geophys. Res. (Space Phys.) 97, 1461–1480.Google Scholar
McPherron, R. L. 1970 Growth phase of magnetospheric substorms. J. Geophys. Res. (Space Phys.) 75, 5592–5599.Google Scholar
Mikhailovskii, A. B. 1998 Instabilities in a Confined Plasma. IOP.Google Scholar
Miyashita, Y., Angelopoulos, V., Fukui, K. & Machida, S. 2018 A case study of near-earth magnetotail conditions at substorm and pseudosubstorm onsets. J. Geophys. Res. (Space Physics) 45, 6353–6361.Google Scholar
Onishchenko, O. G., Pokhotelov, O. A., Krasnoselskikh, V. V. & Shatalov, S. I. 2009 Drift-alfvn waves in space plasmas; theory and mode identification. Ann. Geophys. 27 (2), 639–644.Google Scholar
Pellat, R. 1990 A new approach to magnetic reconnection – magnetic substorms and stellar winds. C. R. Acad. Sci. Paris 311, 45–49.Google Scholar
Roux, A., Perraut, S., Robert, P., Morane, A., Pedersen, A., Korth, A., Kremser, G., Aparicio, B., Rodgers, D. & Pellinen, R. 1991 Plasma sheet instability related to the westward traveling surge. J. Geophys. Res. (Space Phys.) 96, 17697.Google Scholar
Sergeev, V. A., Tanskanen, P., Mursula, K., Korth, A. & Elphic, R. C. 1988 Current sheet thickness in the near-earth plasma sheet during substorm growth phase as inferred from simultaneous magnetotail and ground-based observations. Adv. Space Res. 8, 125–128.Google Scholar
Sharp, W. M., Berk, H. L. & Nielsen, C. E. 1979 Electrostatic bounce modes in mirror plasmas. Phys. Fluids 22, 1975–1987.Google Scholar
Shiokawa, K., Shinohara, I., Mukai, T., Hayakawa, H. & Cheng, C. Z. 2005 Magnetic field fluctuations during substorm-associated dipolarizations in the nightside plasma sheet around $X=-10R_{E}$ . J. Geophys. Res. (Space Phys.) 110, 5212.Google Scholar
Silin, I., Büchner, J. & Zelenyi, L. 2002 Instabilities of collisionless current sheets: theory and simulations. Phys. Plasmas 9, 1104–1112.Google Scholar
Tang, C. L., Li, Z. Y., Angelopoulos, V., Mende, S. B., Glassmeier, K. H., Donovan, E., Russell, C. T. & Lu, L. 2009 THEMIS observations of the near-Earth plasma sheet during a substorm. J. Geophys. Res. (Space Phys.) 114, 9211.Google Scholar
Tur, A., Fruit, G., Louarn, P. & Yanovsky, V. 2014 Kinetic theory of the electron bounce instability in two dimensional current sheets-full electromagnetic treatment. Phys. Plasmas 21 (3), 032113.Google Scholar
Tur, A., Louarn, P. & Yanovsky, V. 2010 Kinetic theory of electrostatic ‘bounce’ modes in two-dimensional current sheets. Phys. Plasmas 17 (10), 102905.Google Scholar
Weiland, J. 2012 Stability and Transport in Magnetic Confinement Systems, vol. 71. Springer Science+Business Media.Google Scholar