Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T19:05:08.445Z Has data issue: false hasContentIssue false
  • English
  • Français

Kinetic infernal modes for Wendelstein 7-X-like $\unicode[STIX]{x1D704}$-profiles

Part of: Focus on Fusion

Published online by Cambridge University Press:  14 November 2019

Alessandro Zocco Open the ORCID record for Alessandro Zocco [Opens in a new window] ,
Alexey Mishchenko Open the ORCID record for Alexey Mishchenko [Opens in a new window]  and
Axel Könies
Alessandro Zocco*
Affiliation:
Max-Planck-Institut für Plasmaphysik, 17489, Greifswald, Germany
Alexey Mishchenko
Affiliation:
Max-Planck-Institut für Plasmaphysik, 17489, Greifswald, Germany
Axel Könies
Affiliation:
Max-Planck-Institut für Plasmaphysik, 17489, Greifswald, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show analytically that for $\unicode[STIX]{x1D704}$-profiles similar to the one of the Wendelstein 7-X stellarator, where $\unicode[STIX]{x1D704}$ is the rotational transform of the equilibrium magnetic field, a highly conducting toroidal plasma is unstable to kinetically mediated pressure-driven long-wavelength reconnecting modes, of the infernal type. The modes are destabilized either by the electron temperature gradient or by a small amount of current, depending on how far from unity the average value of $\unicode[STIX]{x1D704}$ is, which is assumed to be slowly varying. We argue that, for W7-X, a broad mode with toroidal and poloidal mode numbers 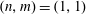$(n,m)=(1,1)$ can be destabilized due to the strong geometric side-band coupling of the resonant kinetic electron response at locations where $\unicode[STIX]{x1D704}$ is rational for harmonics that belong to the mode family of the 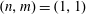$(n,m)=(1,1)$ mode itself. In many regimes, the growth rate is insensitive to the plasma density, thus it is likely to persist in high performance W7-X discharges. For a peaked electron temperature, with a maximum of 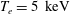$T_{e}=5~\text{keV}$, larger than the ion temperature, 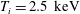$T_{i}=2.5~\text{keV}$, and a density 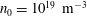$n_{0}=10^{19}~\text{m}^{-3}$, instability is found in regimes which show plasma sawtooth activity, with growth rates of the order of tens of kiloHertz. Frequencies are either electron diamagnetic or of the ideal magnetohydrodynamic type, but sub-Alfvénic. The kinetic infernal mode is thus a good candidate for the explanation of sawtooth oscillations in present-day stellarators and poses a new challenge to the problem of stellarator reactor optimization.

Keywords

fusion plasmaplasma instabilitiesplasma confinement
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 6 , December 2019 , 905850607
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonsen, T. M. & Coppi, B. 1981 Non-asymptotic theory of collisionless reconnecting modes. Phys. Lett. A 81 (6), 335–338.Google Scholar
Ara, G., Basu, B., Coppi, B., Laval, G., Rosenbluth, M. N. & Waddell, B. V. 1978 Magnetic reconnection and $m=1$ oscillations in current carrying plasmas. Ann. Phys. 112 (2), 443–476.Google Scholar
Brunetti, D., Graves, J. P., Cooper, W. A. & Wahlberg, C. 2014 Fast growing resistive two fluid instabilities in hybrid-like tokamak configuration. Plasma Phys. Control. Fusion 56 (7), 075025.Google Scholar
Brunetti, D., Graves, J. P., Halpern, F. D., Luciani, J.-F., Lütjens, H. & Cooper, W. A. 2015 Extended MHD simulations of infernal mode dynamics and coupling to tearing modes. Plasma Phys. Control. Fusion 57 (5), 054002.Google Scholar
Charlton, L. A., Hastie, R. J. & Hender, T. C. 1989 Resistive infernal modes. Phys. Fluids B: Plasma Phys. 1 (4), 798–803.Google Scholar
Connor, J. W., Ham, C. J., Hastie, R. J. & Zocco, A. 2019 Ion Landau damping and drift tearing modes. J. Plasma Phys. 85 (2), 905850204.Google Scholar
Connor, J. W., Hastie, R. J. & Zocco, A. 2012 Unified theory of the semi-collisional tearing mode and internal kink mode in a hot tokamak: implications for sawtooth modelling. Plasma Phys. Control. Fusion 54 (3), 035003.Google Scholar
Coppi, B., Mark, J. W. K., Sugiyama, L. & Bertin, G. 1979 Reconnecting modes in collisonless plasmas. Phys. Rev. Lett. 42, 1058–1061.Google Scholar
Dinklage, A., Beidler, C. D.& the Wendelstein 7-X team 2018 Magnetic configuration effects on the Wendelstein 7-X stellarator. Nat. Phys. 14, 855–860.Google Scholar
Drake, J. F. 1978 Kinetic theory of $m=1$ internal instabilities. Phys. Fluids 21 (10), 1777–1789.Google Scholar
Glasser, A. H., Greene, J. M. & Johnson, J. L. 1975 Resistive instabilities in general toroidal plasma configurations. Phys. Fluids 18 (7), 875–888.Google Scholar
Goedbloed, J. P. & Hagebeuk, H. J. L. 1972 Growth rates of instabilities of a diffuse linear pinch. Phys. Fluids 15 (6), 1090–1101.Google Scholar
Hastie, R. J. 1997 Sawtooth instability in tokamak plasmas. Astrophys. Space Sci. 256 (1), 177–204.Google Scholar
Hastie, R. J. & Hender, T. C. 1988 Toroidal internal kink stability in tokamaks with ultra flat q profiles. Nucl. Fusion 28 (4), 585–594.Google Scholar
Klinger, T., Alonso, A., Bozhenkov, S., Burhenn, R., Dinklage, A., Fuchert, G., Geiger, J., Grulke, O., Langenberg, A., Hirsch, M. et al. & The Wendelstein 7-X Team 2017 Performance and properties of the first plasmas of Wendelstein 7-X. Plasma Phys. Control. Fusion 59 (1), 014018.Google Scholar
Klinger, T., Baylard, C., Beidler, C. D., Boscary, J., Bosch, H. S., Dinklage, A., Hartmann, D., Helander, P., Maassberg, M., Peacock, A. et al. 2013 Towards assembly completion and preparation of experimental campaigns of wendelstein 7-x in the perspective of a path to a stellarator fusion power plant. Fusion Engng Des. 88 (6), 461–465.Google Scholar
Newcomb, W. A. 1960 Hydromagnetic stability of a diffuse linear pinch. Ann. Phys. 10 (2), 232–267.Google Scholar
Nührenberg, C. 1996 Global ideal magnetohydrodynamic stability analysis for the configurational space of Wendelstein 7-X. Phys. Plasmas 3 (6), 2401–2410.Google Scholar
Nührenberg, J. & Zille, R. 1987 Equilibrium and stability of low-shear stellarators. In Theory Fusion Plasmas, pp. 3–23. Compositori Bologna Editrice.Google Scholar
Pegoraro, F., Porcelli, F. & Schep, T. J. 1989 Internal kink modes in the ion-kinetic regime. Phys. Fluids B: Plasma Phys. 1 (2), 364–374.Google Scholar
Porcelli, F. 1987 Viscous resistive magnetic reconnection. Phys. Fluids 30 (6), 1734–1742.Google Scholar
Porcelli, F., Boucher, D. & Rosenbluth, M. N. 1996 Model for the sawtooth period and amplitude. Plasma Phys. Control. Fusion 38 (12), 2163.Google Scholar
Rosenbluth, M. N., Dagazian, R. Y. & Rutherford, P. H. 1973 Nonlinear properties of the internal $m=1$ kink instability in the cylindrical tokamak. Phys. Fluids 16 (11), 1894–1902.Google Scholar
Waelbroeck, F. L. & Hazeltine, R. D. 1988 Stability of low-shear tokamaks. Phys. Fluids 31 (5), 1217–1223.Google Scholar
Zanini, M., Laqua, H. P., Stange, T., Brandt, C., Hirsch, M., Höfel, U., Marushchenko, N., Neuner, U., Rahbarnia, K., Schilling, J. et al. & W7-X Team 2019 ECCD operations in the second experimental campaign at W7-X. Eur. Phys. J. Web Conf. 203, 02013.Google Scholar
Zocco, A., Loureiro, N. F., Dickinson, D., Numata, R. & Roach, C. M. 2015 Kinetic microtearing modes and reconnecting modes in strongly magnetised slab plasmas. Plasma Phys. Control. Fusion 57 (6), 065008.Google Scholar
Zocco, A. & Schekochihin, A. A. 2011 Reduced fluid-kinetic equations for low-frequency dynamics, magnetic reconnection, and electron heating in low-beta plasmas. Phys. Plasmas 18 (10), 102309.Google Scholar