An overview of the neutral beam injectors developed at the Budker Institute of Nuclear Physics in Novosibirsk during the last 10 years is presented. These neutral injectors are used for plasma diagnostics, heating and current drive in modern fusion devices with magnetic confinement. An arc or a radio-frequency (RF) discharge generates a plasma in the ion sources of the injectors, and a positive hydrogen or deuterium ion beam is extracted and accelerated by a multiaperture ion-optical system (IOS). The accelerated ion beam is converted into a neutral one in a gas target. The precision multiaperture IOS with spherically concave electrodes provides ballistic focusing of the neutral beam. The high-energy, high-power beam injector based on negative ions, which is currently under development, is described as well. It comprises a RF negative ion source and a wide-aperture electrostatic accelerator separated from the source by a low-energy beam transport line, thereby improving the injector reliability.

Our earth is immersed in the near-earth space plasma environment, which plays a vital role in protecting our planet against the solar-wind impact and influencing space activities. It is significant to investigate the physical processes dominating the environment, for deepening our scientific understanding of it and improving the ability to forecast the space weather. As a crucial part of the National Major Scientific and Technological Infrastructure–Space Environment Simulation Research Infrastructure (SESRI) in Harbin, the Space Plasma Environment Research Facility (SPERF) builds a system to replicate the near-earth space plasma environment in the laboratory. The system aims to simulate the three-dimensional (3-D) structure and processes of the terrestrial magnetosphere for the first time in the world, providing a unique platform to reveal the physics of the 3-D asymmetric magnetic reconnection relevant to the earth's magnetopause, wave–particle interaction in the earth's radiation belt, particles’ dynamics during the geomagnetic storm, etc. The paper will present the engineering design and construction of the near-earth space plasma simulation system of the SPERF, with a focus on the critical technologies that have been resolved to achieve the scientific goals. Meanwhile, the possible physical issues that can be studied based on the apparatus are sketched briefly. The earth-based system is of great value in understanding the space plasma environment and supporting space exploration.

We describe the interaction of parallel-propagating Alfvén waves with ion-acoustic waves and other Alfvén waves, in magnetized, high-$\beta$ collisionless plasmas. This is accomplished through a combination of analytical theory and numerical fluid simulations of the Chew–Goldberger–Low (CGL) magnetohydrodynamic (MHD) equations closed by Landau-fluid heat fluxes. An asymptotic ordering is employed to simplify the CGL-MHD equations and derive solutions for the deformation of an Alfvén wave that results from its interaction with the pressure anisotropy generated either by an ion-acoustic wave or another, larger-amplitude Alfvén wave. The difference in time scales of acoustic and Alfvénic fluctuations at high-$\beta$ means that interactions that are local in wavenumber space yield little modification to either mode within the time it takes the acoustic wave to Landau damp away. Instead, order-unity changes in the amplitude of Alfvénic fluctuations can result after interacting with frequency-matched acoustic waves. Additionally, we show that the propagation speed of an Alfvén-wave packet in an otherwise homogeneous background is a function of its self-generated pressure anisotropy. This allows for the eventual interaction of separate co-propagating Alfvén-wave packets of differing amplitudes. The results of the CGL-MHD simulations agree well with these predictions, suggesting that theoretical models relying on the interaction of these modes should be reconsidered in certain astrophysical environments. Applications of these results to weak Alfvénic turbulence and to the interaction between the compressive and Alfvénic cascades in strong, collisionless turbulence are also discussed.

Observations, mainly of outbursts in dwarf novae, imply that the anomalous viscosity in highly ionized accretion discs is magnetic in origin and requires that the plasma ${\beta \sim 1}$. Until now, most simulations of the magnetic dynamo in accretion discs have used a local approximation (known as the shearing box). While these simulations demonstrate the possibility of a self-sustaining dynamo, the magnetic activity generated in these models saturates at $\beta \gg 1$. This long-standing discrepancy has previously been attributed to the local approximation itself. There have been recent attempts at simulating magnetic activity in global accretion discs with parameters relevant to the dwarf novae. These too find values of $\beta \gg 1$. We speculate that the tension between these models and the observations may be caused by numerical magnetic diffusivity. As a pedagogical example, we present exact time-dependent solutions for the evolution of weak magnetic fields in an incompressible fluid subject to linear shear and magnetic diffusivity. We find that the maximum factor by which the initial magnetic energy can be increased depends on the magnetic Reynolds number as ${\mathcal {R}}_{m}^{2/3}$. We estimate that current global numerical simulations of dwarf nova discs have numerical magnetic Reynolds numbers around six orders of magnitude less than the physical value found in dwarf nova discs of ${\mathcal {R}}_{m} \sim 10^{10}$. We suggest that, given the current limitations on computing power, expecting to be able to compute realistic dynamo action in observable accretion discs using numerical MHD is, for the time being, a step too far.

Beam–target reactions in fusion plasmas play an important role in both magnetic confinement fusion and inertial confinement fusion in the condition of low-density plasmas with high-velocity interactions. The traditional method for calculating beam–target reaction rate neglects the transport process of incident particles in inhomogeneous plasmas, leading to errors providing that the temperature and density in the transport path of incident particles vary obviously. An improved method considering the transport process is proposed in this paper to eliminate the deficiencies. Then the method is employed in high-speed plasma collision studies. When the initial plasma density and temperature are set to $0.5\,{\rm g}\,{\rm cm}^{-3}$ and 100 eV, it is found that the beam–target reaction rate calculated by the traditional method is almost identical to that by our method if the collision velocity is less than 600 km s$^{-1}$. However, the traditional method is not suitable for study as the collision velocity gets higher, inducing obvious differences, which can reach 70 % at 1000 km s$^{-1}$. The improved method will make large corrections to evaluate the importance of the non-negligible beam–target reaction for inertial confinement fusion schemes with large implosion velocity such as double-cone ignition and impact ignition, in which the high-speed plasmas collide with each other to realize plasma ignition.

Electron-cyclotron resonance heating (ECRH) is the main heating mechanism in the Wendelstein 7-X (W7-X) stellarator. Although second-harmonic ECRH (X2) has been used routinely for plasma startup, startup at third harmonic (X3) is known to be much more difficult. In this work, we investigate the energy gain of particles during nonlinear wave–particle interaction for conditions relevant to second- and third-harmonic startups in W7-X. We take into account both the beam and the ambient magnetic field inhomogeneities. The latter is shown to significantly increase the mean energy gain resulting from a single wave–particle resonant interaction. In W7-X-like conditions, the improvement in maximum gained energy is up to 4 times the analogous uniform magnetic field case. However, this improvement is not enough to ensure X3 startup. The optimal magnetic field inhomogeneity length scale for average energy gain and start up in W7-X-like conditions is found to be in the range of $1$ to $3\ {\rm km}^{-1}$. A possibility of using multiple beams with neighbouring resonances is also considered. A considerable enhancement of the energy gain is demonstrated.

The particle-in-cell (PIC) method is successfully used to study magnetized plasmas. However, this requires large computational costs and limits simulations to short physical run times and often to set-ups of less than three spatial dimensions. Traditionally, this is circumvented either via hybrid-PIC methods (adopting massless electrons) or via magneto-hydrodynamic-PIC methods (modelling the background plasma as a single charge-neutral magneto-hydrodynamical fluid). Because both methods preclude modelling important plasma-kinetic effects, we introduce a new fluid-PIC code that couples a fully explicit and charge-conserving multi-fluid solver to the PIC code SHARP through a current-coupling scheme and solve the full set of Maxwell's equations. This avoids simplifications typically adopted for Ohm's law and enables us to fully resolve the electron temporal and spatial scales while retaining the versatility of initializing any number of ion, electron or neutral species with arbitrary velocity distributions. The fluid solver includes closures emulating Landau damping so that we can account for this important kinetic process in our fluid species. Our fluid-PIC code is second-order accurate in space and time. The code is successfully validated against several test problems, including the stability and accuracy of shocks and the dispersion relation and damping rates of waves in unmagnetized and magnetized plasmas. It also matches growth rates and saturation levels of the gyro-scale and intermediate-scale instabilities driven by drifting charged particles in magnetized thermal background plasmas in comparison with linear theory and PIC simulations. This new fluid-SHARP code is specially designed for studying high-energy cosmic rays interacting with thermal plasmas over macroscopic time scales.

The excitation conditions of the magnetorotational instability (MRI) are studied for axially unbounded Taylor–Couette (TC) flows of various gap widths between the cylinders. The cylinders are considered as made from both perfect-conducting or insulating material and the conducting fluid with a finite but small magnetic Prandtl number rotates with a quasi-Keplerian velocity profile. The solutions are optimized with respect to the wavenumber and the Reynolds number of the rotation of the inner cylinder. For the axisymmetric modes, we find the critical Lundquist number of the applied axial magnetic field: the lower, the wider the gap between the cylinders. A similar result is obtained for the induced cell structure: the wider the gap, the more spherical the cells are. The marginal rotation rate of the inner cylinder – for a fixed size of the outer cylinder – always possesses a minimum for not too wide and not too narrow gap widths. For perfect-conducting walls the minimum lies at $r_{{\rm in}}\simeq 0.4$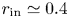, where $r_{{\rm in}}$ 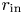is the ratio of the radii of the two rotating cylinders. The lowest magnetic field amplitudes to excite the instability are required for TC flows between perfect-conducting cylinders with gaps corresponding to $r_{{\rm in}}\simeq ~0.2$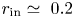. For even wider and also for very thin gaps the needed magnetic fields and rotation frequencies are shown to become rather huge. Also the non-axisymmetric modes with $|m|=1$ 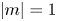have been considered. Their excitation generally requires stronger magnetic fields and higher magnetic Reynolds numbers in comparison with those for the axisymmetric modes. If TC experiments with too slow rotation for the applied magnetic fields yield unstable modes of any azimuthal symmetry, such as the currently reported Princeton experiment (Wang et al., Phys. Rev. Lett., vol. 129, 115001), then also other players, including axial boundary effects, than the MRI-typical linear combination of current-free fields and differential rotation should be in the game.

We analysed the excitation of a surface magnetoplasmon wave by the mode conversion of a p-polarized laser beam over a rippled semiconductor (n-type)-free space interface. The pump surface magnetoplasmon wave exerts a ponderomotive force on the free electrons in the semiconductor, imparting a linear oscillatory velocity at the laser modulation frequency to them. This linear oscillatory velocity couples with the modulated electron density to produce a current density, which develops a resonant surface magnetoplasmon wave in the terahertz region. The amplitude of the terahertz surface magnetoplasmon wave can be tuneable with an external magnetic field and the semiconductor's temperature.

The extended guiding-centre Lagrangian equations of motion are derived by the Lie-transform perturbation method under the assumption of time-dependent and inhomogeneous electric and magnetic fields that satisfy the standard guiding-centre space–time orderings. Polarization effects are introduced into the Lagrangian dynamics by the inclusion of the polarization drift velocity in the guiding-centre velocity and the appearance of finite-Larmor-radius corrections in the guiding-centre Hamiltonian and guiding-centre Poisson bracket.

An open problem of the derivation of the relativistic Vlasov equation for systems of charged particles moving with velocities up to the speed of light and creating the electromagnetic field in accordance with the full set of the Maxwell equations is considered. Moreover, the method of derivation is illustrated on the non-relativistic kinetic model. Independent derivation of the relativistic hydrodynamics is also demonstrated. The key role of these derivations of the hydrodynamic and kinetic equations includes the explicit operator of averaging on the physically infinitesimal volume suggested by L.S. Kuzmenkov.

The two-time energy spectrum of weak magnetohydrodynamic turbulence is found by applying a wave-turbulence closure to the cumulant hierarchy constructed from the dynamical equations. Solutions are facilitated via asymptotic expansions in terms of the small parameter $\varepsilon$, describing the ratio of time scales corresponding to Alfvénic propagation and nonlinear interactions between counter-propagating Alfvén waves. The strength of nonlinearity at a given spatial scale is further quantified by an integration over all possible delta-correlated modes compliant in a given set of three-wave interactions that are associated with energy flux through the said scale. The wave-turbulence closure for the two-time spectrum uncovers a secularity occurring on a time scale of order $\varepsilon ^{-2}$, and the asymptotic expansion for the spectrum is reordered in a manner comparable to the one-time case. It is shown that for the regime of stationary turbulence, the two-time energy spectrum exponentially decays on a lagged time scale $(\varepsilon ^2 \gamma _k^s)^{-1}$ in proportion to the strength of the associated three-wave interactions, characterized by nonlinear decorrelation frequency $\gamma _k^s$. The scaling of the form $k_{\perp } v_0 \chi _0$ exhibited by this frequency is reminiscent of random sweeping by the outer scale with characteristic fluctuation velocity $v_0$ that is modified due to competition with Alfvénic propagation (characterized by $\chi _0$) at the said scale. A brief calculation of frequency broadening of the power spectrum due to nonlinear interactions is also presented.

The impact of an edge radial electric field on the particle orbits and the orbital spectrum in an axisymmetric toroidal magnetic equilibrium is investigated using a guiding centre canonical formalism. Poloidal and bounce/transit-averaged toroidal precession frequencies are calculated, highlighting the role of the radial electric field. The radial electric field is shown to drastically modify the resonance conditions between particles with certain kinetic characteristics and specific perturbative non-axisymmetric modes, and to enable the formation of transport barriers. The locations of the resonances and the transport barriers that determine the particle, energy and momentum transport are shown to be accurately pinpointed in the phase space by employing the calculated orbital frequencies.

The self-consistent propagation of electrical impulses and of the accompanying distortions of the electron surface in the framework of a cold plasma model with a sharp boundary has been described with help of a derived system of two equations. The method of ‘shallow water theory’ has been applied for the case of bounded plasma and deriving an equation with which to link the spatial and temporal structures and evolution of the boundary curvature and the surface charge. Under certain conditions, such perturbations can propagate along the boundary without changing their shape for a long distance. An approximate analytical solution has been found, and numerical calculations have been performed. Mutual connections between basic parameters of the considered perturbations (velocity components, electrostatic field, etc.) have been presented.

A conducting cylinder with a uniform magnetic field along its axis and radial temperature gradient is considered at the stationary state. At large temperature gradients the azimuthal Hall electrical current creates an axial magnetic field whose strength may be comparable with the original one. It is shown that the magnetic field, generated by the azimuthal Hall current, leads to the decrease of a magnetic field originated by external sources, and this suppression increases with an increase of the electromotive force, connected with thermodiffusion. Obtained results can help to investigate the influence of the Hall current on the coupled magnetothermal evolution of magnetic and electric fields in neutron stars, white dwarfs and, possibly, in laboratory facilities.

Generalising the Elsässer variables, we introduce the $Q$-variables. These are more flexible than the Elsässer variables, because they also allow us to track waves with phase speeds different than the Alfvén speed. We rewrite the magnetohydrodynamics (MHD) equations with these $Q$-variables. We consider also the linearised version of the resulting MHD equations in a uniform plasma, and recover the classical Alfvén waves, but also separate the fast and slow magnetosonic waves into upward- and downward-propagating waves. Moreover, we show that the $Q$-variables may also track the upward- and downward-propagating surface Alfvén waves in a non-uniform plasma, displaying the power of our generalisation. In the end, we lay the mathematical framework for driving solar wind models with a multitude of wave drivers.

We investigate the effects of different guard geometries on the currents to needle-type Langmuir probes. The results are based on particle-in-cell numerical simulations. We show that if the guard length is less than 6–8 Debye lengths there can be a significant effect on the currents to the probe. A guard radius should not be larger than the Debye length, otherwise it can also significantly affect the currents. However, since guard radii are often close to the probe radius, the second condition is usually satisfied.

This study investigates the effect of a transverse magnetic field on high-voltage pulsed discharge in helium at a pressure of 30 Torr. A simple two-dimensional fluid model that describes the high-voltage pulsed discharge in helium in a transverse weak magnetic field (B = 0.4 T) is presented, which uses an empirical relation to account for the magnetic field. The results of using the empirical relation for the effective field agree well with the experimental results. The dynamics of discharge development in the presence of the magnetic field is also investigated. The magnetic field does not significantly affect the gas-discharge development dynamics in helium at a pressure of 30 Torr.

The theory of the terahertz (THz) waves emission from a near-critical plasma slab under the action of the focused p-polarized laser pulse is developed. The spectral, angular and energy characteristics of the THz signal are studied as functions of the focusing degree and the incidence angle of laser radiation, as well as the density and thickness of the plasma slab. It is shown that the extremely strong increase in the energy of the THz signal (up to millijoule level) and conversion rate (up to 10 %) occurs at the almost normal incidence of the ultra-short, tightly focused p-polarized laser pulse on the thin plasma slab with the near-critical density and rare electron collisions.

BOUT++ turbulence simulations were performed to investigate the impact of turbulence spreading on the edge localized mode (ELM) size and divertor heat flux width $({\lambda _q})$ broadening in small ELM regimes. This study is motivated by EAST experiments. BOUT++ linear simulations of a pedestal radial electric field (Er) scan show that the dominant toroidal number mode (n) shifts from high-n to low-n, with a narrow mode spectrum, and the maximum linear growth rate increases as the pedestal Er well deepens. The nonlinear simulations show that as the net E × B pedestal flow increases, the pressure fluctuation level and its inward penetration beyond the top of the pedestal both increase. This leads to a transition from small ELMs to large ELMs. Both inward and outward turbulence spreading are sensitive to the scrape-off-layer (SOL) plasma profiles. The inward turbulence spreading increases for the steep SOL profiles, leading to increasing pedestal energy loss in the small ELM regime. The SOL width $({\lambda _q})$ is significantly broadened progressing from the ELM-free to small ELM regime, due to the onset of strong radial turbulent transport. The extent of the SOL width $({\lambda _q})$ broadening depends strongly on outward turbulence spreading. The fluctuation energy intensity flux ${\varGamma _\varepsilon }$ at the separatrix can be enhanced by increasing either pedestal Er flow shear or local SOL pressure gradient. The ${\lambda _q}$ is broadened as the fluctuation energy intensity flux ${\varGamma _\varepsilon }$ at the last close flux surface (LCFS) increases. Local SOL E × B flow shear will restrain outward turbulence spreading and the associated heat flux width broadening. Operating in H-mode with small ELMs has the potential to solve two critical problems: reducing the ELM size and broadening the SOL width.