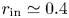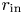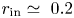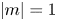1. Introduction and motivation
Taylor–Couette (TC) flows with conducting fluids between two rotating cylinders are favorable for an experimental realization of the various versions of the magnetorotational instability (MRI) for which the applied magnetic field is always current-free (Velikhov Reference Velikhov1959; Ji, Goodman & Kageyama Reference Ji, Goodman and Kageyama2001; Rüdiger & Zhang Reference Rüdiger and Zhang2001; Schartman, Ji & Burin Reference Schartman, Ji and Burin2009; Schartman et al. Reference Schartman, Ji, Burin and Goodman2012). If the field is spiral rather than axial, the necessary Reynolds numbers and Hartmann numbers are surprisingly small (Hollerbach & Rüdiger Reference Hollerbach and Rüdiger2005; Rüdiger et al. Reference Rüdiger, Hollerbach, Stefani, Gundrum, Gerbeth and Rosner2006) which made it possible to investigate the corresponding helical version of MRI (HMRI) with the Promise experiment (Stefani et al. Reference Stefani, Gundrum, Gerbeth, Rüdiger, Schultz, Szklarski and Hollerbach2006). The resulting instability modes are axisymmetric and they are migrating along the rotation axis. The closely related azimuthal MRI (AMRI) appears when working with current-free toroidal fields for which the unstable modes are non-axisymmetric (Ogilvie & Pringle Reference Ogilvie and Pringle1996; Hollerbach, Teeluck & Rüdiger Reference Hollerbach, Teeluck and Rüdiger2010; Seilmayer et al. Reference Seilmayer, Galindo, Gerbeth, Gundrum, Stefani, Gellert, Rüdiger, Schultz and Hollerbach2014).
The mentioned experiments have used one and the same container construction where the inner radius was 50 % of the outer radius, i.e. $r_{{\rm in}}=R_{{\rm in}}/R_{{\rm out}}=0.5$![]() . For this geometry the rotation law $\varOmega \propto R^{-q}$
. For this geometry the rotation law $\varOmega \propto R^{-q}$![]() leads to a shear $\mu =\varOmega _{{\rm out}}/\varOmega _{{\rm in}}$
leads to a shear $\mu =\varOmega _{{\rm out}}/\varOmega _{{\rm in}}$![]() for quasi-Keplerian rotation with $q=1.5$
for quasi-Keplerian rotation with $q=1.5$![]() of $\mu =0.35$
of $\mu =0.35$![]() . In a recent paper the Princeton group presented experimental results related to the standard version of MRI (SMRI), with a purely axial field being applied, using a container with $r_{{\rm in}}=0.35$
. In a recent paper the Princeton group presented experimental results related to the standard version of MRI (SMRI), with a purely axial field being applied, using a container with $r_{{\rm in}}=0.35$![]() and the aspect ratio $\varGamma =H/(R_{{\rm out}}-R_{{\rm in}})=2.1$
and the aspect ratio $\varGamma =H/(R_{{\rm out}}-R_{{\rm in}})=2.1$![]() . The flow between the cylinders is described by $\mu =0.19$
. The flow between the cylinders is described by $\mu =0.19$![]() , while the quasi-Keplerian flow in such a container is defined by $\mu =0.21$
, while the quasi-Keplerian flow in such a container is defined by $\mu =0.21$![]() (Wang et al. Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022b).
(Wang et al. Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022b).
After our previous numerical results for $r_{{\rm in}}=0.5$![]() , for very small magnetic Prandtl number and for perfectly conducting walls, the absolute minimum of the magnetic Reynolds number for the excitation of marginal instability was 21.3 for a shear flow with $\mu =0.33$
, for very small magnetic Prandtl number and for perfectly conducting walls, the absolute minimum of the magnetic Reynolds number for the excitation of marginal instability was 21.3 for a shear flow with $\mu =0.33$![]() , which is somewhat steeper than the Keplerian rotation law with $\mu =0.35$
, which is somewhat steeper than the Keplerian rotation law with $\mu =0.35$![]() (Rüdiger et al. Reference Rüdiger, Gellert, Hollerbach, Schultz and Stefani2018a). Both of these slightly super-Keplerian rotation laws follow $\mu =r_{{\rm in}}^{q}$
(Rüdiger et al. Reference Rüdiger, Gellert, Hollerbach, Schultz and Stefani2018a). Both of these slightly super-Keplerian rotation laws follow $\mu =r_{{\rm in}}^{q}$![]() with $q=1.59$
with $q=1.59$![]() .
.
The model of a homogeneous fluid contained between two vertically unbounded rotating cylinders is used with a uniform magnetic field parallel to the rotation axis. For viscous flows the general form of the rotation law $\varOmega (R)$![]() of the fluid is
of the fluid is
where $a$![]() and $b$
and $b$![]() are the two constants related to the angular velocities $\varOmega _{\rm {in}}$
are the two constants related to the angular velocities $\varOmega _{\rm {in}}$![]() and $\varOmega _{\rm {out}}$
and $\varOmega _{\rm {out}}$![]() , with which the inner and the outer cylinders are rotating, and $R$
, with which the inner and the outer cylinders are rotating, and $R$![]() is the distance from the rotation axis. If $R_{\rm {in}}$
is the distance from the rotation axis. If $R_{\rm {in}}$![]() and $R_{\rm {out}}$
and $R_{\rm {out}}$![]() ($R_{\rm {out}}>R_{\rm {in}}$
($R_{\rm {out}}>R_{\rm {in}}$![]() ) are the radii of the two cylinders, then
) are the radii of the two cylinders, then
with the above defined geometry parameters $\mu$![]() and $r_{{\rm in}}$
and $r_{{\rm in}}$![]() . Following the Rayleigh stability criterion,
. Following the Rayleigh stability criterion,
rotation laws are hydrodynamically stable for $a>0$![]() , i.e. $\mu >r_{{\rm in}}^2$
, i.e. $\mu >r_{{\rm in}}^2$![]() . They should in particular be stable for a resting inner cylinder, i.e. $\mu \to \infty$
. They should in particular be stable for a resting inner cylinder, i.e. $\mu \to \infty$![]() (superrotation).
(superrotation).
The present paper has two motivations. The first one concerns the question of the dependence of the eigenvalues on the gap width of the container. The ratio $r_{{\rm in}}$![]() of the two-cylinder radii is the only free parameter describing the geometry of the axially unbounded container. It is so far unknown how the gap width determines the critical rotation rate for a given magnetic field, and also the wavenumber of the excited instability pattern. The latter result will have consequences for necessary vertical extension of a possible experimental set-up.
of the two-cylinder radii is the only free parameter describing the geometry of the axially unbounded container. It is so far unknown how the gap width determines the critical rotation rate for a given magnetic field, and also the wavenumber of the excited instability pattern. The latter result will have consequences for necessary vertical extension of a possible experimental set-up.
We work with the magnetic Prandtl number
with $\nu$![]() being the kinematic viscosity and $\eta$
being the kinematic viscosity and $\eta$![]() the magnetic diffusivity. The equations are solved for the very small magnetic Prandtl number $Pm =10^{-5}$
the magnetic diffusivity. The equations are solved for the very small magnetic Prandtl number $Pm =10^{-5}$![]() close to the value for liquid sodium. For small magnetic Prandtl numbers the excitation conditions for the standard magnetorotational instability only depend on the microscopic magnetic diffusivity rather than the molecular viscosity, so that even $Pm$
close to the value for liquid sodium. For small magnetic Prandtl numbers the excitation conditions for the standard magnetorotational instability only depend on the microscopic magnetic diffusivity rather than the molecular viscosity, so that even $Pm$![]() does not play a role (Rüdiger & Shalybkov Reference Rüdiger and Shalybkov2002). The ratio of the container wall radii is varied from $r_{{\rm in}}= 0.1$
does not play a role (Rüdiger & Shalybkov Reference Rüdiger and Shalybkov2002). The ratio of the container wall radii is varied from $r_{{\rm in}}= 0.1$![]() to $r_{{\rm in}}= 0.9$
to $r_{{\rm in}}= 0.9$![]() . We shall see that between these values the critical magnetic Reynolds number of rotation possesses a minimum while the critical Lundquist number of the applied magnetic field linearly grows with $r_{{\rm in}}$
. We shall see that between these values the critical magnetic Reynolds number of rotation possesses a minimum while the critical Lundquist number of the applied magnetic field linearly grows with $r_{{\rm in}}$![]() .
.
Our second question is the difference of the excitation conditions for axisymmetric and non-axisymmetric modes. Though it is widely known that the mode with the easiest excitation is the axisymmetric one, it is still important to know how much more difficult the excitation of a non-axisymmetric mode is.
2. Basic equations
The magnetohydrodynamics equations which have to be solved are
and
with the electric current
and with $\boldsymbol {\nabla } {\boldsymbol u} = \boldsymbol {\nabla } {\boldsymbol B} = 0$![]() . They must be considered in a cylindrical geometry with $R$
. They must be considered in a cylindrical geometry with $R$![]() , $\phi$
, $\phi$![]() and $z$
and $z$![]() as the coordinates. A viscous electric-conducting incompressible fluid between two rotating infinite cylinders in the presence of a uniform magnetic field parallel to the rotation axis leads to the basic solution $U_R=U_z=B_R=B_\phi =0, B_z=B_0={\rm const.}\ {\rm and}\ U_\phi =a R+b/R$
as the coordinates. A viscous electric-conducting incompressible fluid between two rotating infinite cylinders in the presence of a uniform magnetic field parallel to the rotation axis leads to the basic solution $U_R=U_z=B_R=B_\phi =0, B_z=B_0={\rm const.}\ {\rm and}\ U_\phi =a R+b/R$![]() , with ${\boldsymbol U}$
, with ${\boldsymbol U}$![]() as the flow and ${\boldsymbol B}$
as the flow and ${\boldsymbol B}$![]() as the magnetic field. We are interested in the stability of this solution. The perturbed state of the flow may be described by $u'_R,\ u'_\phi,\ u'_z,\ p', B'_R,\ B'_\phi,\ B'_z$
as the magnetic field. We are interested in the stability of this solution. The perturbed state of the flow may be described by $u'_R,\ u'_\phi,\ u'_z,\ p', B'_R,\ B'_\phi,\ B'_z$![]() with $p'$
with $p'$![]() as the pressure perturbation.
as the pressure perturbation.
In the following only the linear stability problem will be considered. By expansion of the disturbances into normal modes the solutions of the linearized equations are of the form
From here on all dashes are being omitted from the symbols of fluctuating quantities. The marginal stability line is defined where the imaginary part ${\rm Im}({\omega })$![]() vanishes. We shall always use the geometrical average
vanishes. We shall always use the geometrical average
as the unit of length, $\eta /R_0$![]() as the unit of velocity and $B_0$
as the unit of velocity and $B_0$![]() as the unit of the magnetic field. We note the rather weak dependence of $R_0$
as the unit of the magnetic field. We note the rather weak dependence of $R_0$![]() on the value of $r_{{\rm in}}$
on the value of $r_{{\rm in}}$![]() as long as $0.2\leq r _{{\rm in}} \leq 0.8$
as long as $0.2\leq r _{{\rm in}} \leq 0.8$![]() . The $R_0$
. The $R_0$![]() only becomes small for $r_{{\rm in}}\to 0$
only becomes small for $r_{{\rm in}}\to 0$![]() or for $r_{{\rm in}}\to 1$
or for $r_{{\rm in}}\to 1$![]() , i.e. for very wide or for very narrow gaps between the cylinders. Its maximum $R_0=0.5 R_{\rm out}$
, i.e. for very wide or for very narrow gaps between the cylinders. Its maximum $R_0=0.5 R_{\rm out}$![]() is reached for $r_{{\rm in}}=0.5$
is reached for $r_{{\rm in}}=0.5$![]() . In order to denormalize quantities, $R_0^{-1}$
. In order to denormalize quantities, $R_0^{-1}$![]() is used as the unit of wavenumbers and $\nu /R_0^2$
is used as the unit of wavenumbers and $\nu /R_0^2$![]() as the unit of frequencies.
as the unit of frequencies.
Using the same symbols for normalized quantities, the equations can be written as a system of 10 equations of first order, i.e.




where $X_1$![]() is given by
is given by
with $P$![]() as the pressure fluctuation.
as the pressure fluctuation.
Here the dimensionless Reynolds number $Re$![]() and the Hartmann number $Ha$
and the Hartmann number $Ha$![]() are defined as
are defined as
For given Hartmann number and magnetic Prandtl number we shall compute with a linear theory the critical Reynolds number of the rotation of the inner cylinder, also for various azimuthal mode numbers $m$![]() . We shall see that the excitation conditions for SMRI can easily be expressed by the magnetic Reynolds number $Rm$
. We shall see that the excitation conditions for SMRI can easily be expressed by the magnetic Reynolds number $Rm$![]() and the Lundquist number $S$
and the Lundquist number $S$![]() , with the definitions
, with the definitions
without influence of the molecular viscosity. The ratio of both quantities forms the magnetic Mach number of rotation,
which describes the strength of the rotation normalized with the applied magnetic field. The majority of cosmic objects are characterized by magnetic Mach numbers larger than unity (except the magnetars). We shall discuss the relationship of the magnetic Mach number on the normalized gap width between the cylinders only for the characteristic constellation where the Reynolds number is minimal for the excitation of the instability.
The actual calculations were specifically carried out for the small magnetic Prandtl number $Pm=10^{-5}$![]() , but the obtained results for $Rm$
, but the obtained results for $Rm$![]() and $S$
and $S$![]() are also correct for even smaller $Pm$
are also correct for even smaller $Pm$![]() (Rüdiger & Shalybkov Reference Rüdiger and Shalybkov2002). The reason is that for small $Pm$
(Rüdiger & Shalybkov Reference Rüdiger and Shalybkov2002). The reason is that for small $Pm$![]() the critical Reynolds number varies with $1/Pm$
the critical Reynolds number varies with $1/Pm$![]() so that the magnetic Reynolds number $Rm\simeq$
so that the magnetic Reynolds number $Rm\simeq$![]() const. It is clear, therefore, that for $Pm=0$
const. It is clear, therefore, that for $Pm=0$![]() the magnetorotational instability does not exist.
the magnetorotational instability does not exist.
3. Boundary conditions
For the solution of the differential equations of 10th order a set of 10 boundary conditions is needed. No-slip conditions for the velocity on the walls are always used, i.e. $u_R=u_\phi ={\rm d} u_R/{\rm d} R=0.$![]() The magnetic boundary conditions depend on the electrical properties of the walls. For perfectly conducting walls the tangential currents and the radial component of the magnetic field vanish, hence ${\rm d} B_\phi /{\rm d} R + B_\phi /R = B_R = 0$
The magnetic boundary conditions depend on the electrical properties of the walls. For perfectly conducting walls the tangential currents and the radial component of the magnetic field vanish, hence ${\rm d} B_\phi /{\rm d} R + B_\phi /R = B_R = 0$![]() . These boundary conditions hold for both $R=R_{\rm in}$
. These boundary conditions hold for both $R=R_{\rm in}$![]() and $R=R_{\rm out}$
and $R=R_{\rm out}$![]() .
.
For insulating walls the magnetic boundary conditions are different at $R_{\rm in}$![]() and $R_{\rm out}$
and $R_{\rm out}$![]() , i.e. for $R_{\rm in}$
, i.e. for $R_{\rm in}$![]()
and for $R=R_{\rm out}$![]()
where $I_m$![]() and $K_m$
and $K_m$![]() are the modified Bessel functions. The condition for the toroidal field is $k R B_\phi =m B_z$
are the modified Bessel functions. The condition for the toroidal field is $k R B_\phi =m B_z$![]() (Rüdiger, Schultz & Shalybkov Reference Rüdiger, Schultz and Shalybkov2003). Neutral stability of the solutions is reached for vanishing ${\rm Im}(\omega )$
(Rüdiger, Schultz & Shalybkov Reference Rüdiger, Schultz and Shalybkov2003). Neutral stability of the solutions is reached for vanishing ${\rm Im}(\omega )$![]() .
.
The homogeneous set of (2.6)–(2.13) with the boundary conditions included determine the eigenvalue problem of the form $\mathcal {L}(k, m, {Re}, \omega )=0$![]() for given $Pm$
for given $Pm$![]() and $Ha$
and $Ha$![]() . Here $\mathcal {L}$
. Here $\mathcal {L}$![]() is a complex quantity, both its real part and its imaginary part must vanish for the critical Reynolds number. For non-axisymmetric modes the real part, ${{\rm Re}}(\omega )$
is a complex quantity, both its real part and its imaginary part must vanish for the critical Reynolds number. For non-axisymmetric modes the real part, ${{\rm Re}}(\omega )$![]() , of $\omega$
, of $\omega$![]() describes a drift of the pattern along the azimuth. It is the second quantity that is fixed by the complex eigenequation. For a fixed Hartmann number, a fixed Prandtl number and a given vertical wavenumber, we also find the critical $Re$
describes a drift of the pattern along the azimuth. It is the second quantity that is fixed by the complex eigenequation. For a fixed Hartmann number, a fixed Prandtl number and a given vertical wavenumber, we also find the critical $Re$![]() of the system. It is minimal for a certain wavenumber defining a marginally unstable mode. The corresponding value $Re_{\rm min}$
of the system. It is minimal for a certain wavenumber defining a marginally unstable mode. The corresponding value $Re_{\rm min}$![]() is the minimal Reynolds number if $Ha$
is the minimal Reynolds number if $Ha$![]() is varied and $Ha_{\rm min}$
is varied and $Ha_{\rm min}$![]() is the Hartmann number for which the $Re_{\rm min}$
is the Hartmann number for which the $Re_{\rm min}$![]() occurs. For oscillatory axisymmetric and drifting non-axisymmetric modes the real part of the frequency $\omega$
occurs. For oscillatory axisymmetric and drifting non-axisymmetric modes the real part of the frequency $\omega$![]() is the second eigenvalue fixed by the eigenequation.
is the second eigenvalue fixed by the eigenequation.
4. General results
For perfect-conducting boundary conditions the resulting curves of marginal stability are given in figure 1 and for vacuum boundary conditions in figure 2. Figures 1(a) and 2(a) present the magnetic Reynolds numbers (minimized with the wavenumber) and figures 1(b) and 2(b) give the resulting wavenumbers, in both cases as functions of the Lundquist number. The dashed lines belong to the azimuthally drifting non-axisymmetric modes with $|m|=1$![]() . Generally, the latter require higher values $Rm_{\rm min}$
. Generally, the latter require higher values $Rm_{\rm min}$![]() than the axisymmetric modes. The curves for $m=0$
than the axisymmetric modes. The curves for $m=0$![]() exhibit their typical shape: they are rather steep for $S< S_{\rm min}$
exhibit their typical shape: they are rather steep for $S< S_{\rm min}$![]() but they are much flatter for $S>S_{\rm min}$
but they are much flatter for $S>S_{\rm min}$![]() , where $S_{\rm min}$
, where $S_{\rm min}$![]() is taken at the minimum of the function $Rm=Rm(S)$
is taken at the minimum of the function $Rm=Rm(S)$![]() . For $S=O(1)$
. For $S=O(1)$![]() the influence of the microscopic diffusion stops the existence of SMRI, while for much larger $S$
the influence of the microscopic diffusion stops the existence of SMRI, while for much larger $S$![]() it is damped by too strong external magnetic fields.
it is damped by too strong external magnetic fields.

Figure 1. (a) Stability map for $m=0$![]() (solid lines): $r_{{\rm in}}=0.1$
(solid lines): $r_{{\rm in}}=0.1$![]() , $r_{{\rm in}}=0.3$
, $r_{{\rm in}}=0.3$![]() (green); $r_{{\rm in}}=0.5$
(green); $r_{{\rm in}}=0.5$![]() (red); $r_{{\rm in}}=0.7$
(red); $r_{{\rm in}}=0.7$![]() . For $m=1$
. For $m=1$![]() (dashed lines): $r_{{\rm in}}=0.3$
(dashed lines): $r_{{\rm in}}=0.3$![]() (green); $r_{{\rm in}}=0.4$
(green); $r_{{\rm in}}=0.4$![]() $r_{{\rm in}}=0.5$
$r_{{\rm in}}=0.5$![]() (red); $r_{{\rm in}}=0.6$
(red); $r_{{\rm in}}=0.6$![]() . (b) The corresponding axial wavenumbers. Quasi-Keplerian differential rotation, $Pm=10^{-5}$
. (b) The corresponding axial wavenumbers. Quasi-Keplerian differential rotation, $Pm=10^{-5}$![]() , perfect-conducting cylinder material.
, perfect-conducting cylinder material.

Figure 2. The lines of neutral stability for containers with insulating cylinders. (a) Stability map for $m=0$![]() (solid lines) with $r_{{\rm in}}=0.1$
(solid lines) with $r_{{\rm in}}=0.1$![]() , $r_{{\rm in}}=0.3$
, $r_{{\rm in}}=0.3$![]() (green); $r_{{\rm in}}=0.5$
(green); $r_{{\rm in}}=0.5$![]() (red); $r_{{\rm in}}=0.7$
(red); $r_{{\rm in}}=0.7$![]() , $r_{{\rm in}}=0.9$
, $r_{{\rm in}}=0.9$![]() (blue); and for $m=1$
(blue); and for $m=1$![]() (dashed lines) with $r_{{\rm in}}=0.3$
(dashed lines) with $r_{{\rm in}}=0.3$![]() (green); $r_{{\rm in}}=0.5$
(green); $r_{{\rm in}}=0.5$![]() (red); $r_{{\rm in}}=0.7$
(red); $r_{{\rm in}}=0.7$![]() . (b) The corresponding axial wavenumbers. Quasi-Keplerian differential rotation, $Pm=10^{-5}$
. (b) The corresponding axial wavenumbers. Quasi-Keplerian differential rotation, $Pm=10^{-5}$![]() .
.
The curves of marginal stability for the axisymmetric modes only possess a lower limit of the critical Reynolds number above which the flow becomes unstable. In opposition the curves for the non-axisymmetric modes always possess a lower and an upper limit of the critical Reynolds numbers. Non-axisymmetric magnetic modes are generally stabilized by too fast shearing flow (Rädler Reference Rädler1986; Rüdiger et al. Reference Rüdiger, Gellert, Hollerbach, Schultz and Stefani2018a).
4.1. Medium gaps
The minimum $Rm_{\rm min}$![]() in figure 1 for medium gap widths approximately behave according to $(1-r_{{\rm in}})Rm_{\rm min}\simeq 13$
in figure 1 for medium gap widths approximately behave according to $(1-r_{{\rm in}})Rm_{\rm min}\simeq 13$![]() (see table 1). This relation implies that the minimal rotation rates of the inner cylinder for the considered gaps behave like $\varOmega _{\rm in}\propto 1/(1-r_{{\rm in}})$
(see table 1). This relation implies that the minimal rotation rates of the inner cylinder for the considered gaps behave like $\varOmega _{\rm in}\propto 1/(1-r_{{\rm in}})$![]() , i.e. in containers with wider gaps the instability is easier to excite. For very wide gaps, however, both the magnetic Reynolds number as well as the needed rotation rate of the inner cylinder grow to very large values. Minimal rotation rates are only possible for experiments with medium $r_{{\rm in}}$
, i.e. in containers with wider gaps the instability is easier to excite. For very wide gaps, however, both the magnetic Reynolds number as well as the needed rotation rate of the inner cylinder grow to very large values. Minimal rotation rates are only possible for experiments with medium $r_{{\rm in}}$![]() .
.
Table 1. The coordinates of the minima of the profiles in figures 1(a) and 2(a) for several radii the inner cylinder for different boundary conditions (left, perfect conduction; right, vacuum); $m=0$![]() , $Pm=10^{-5}$
, $Pm=10^{-5}$![]() . All models for quasi-Keplerian rotation laws.
. All models for quasi-Keplerian rotation laws.

In table 1 the resulting numbers $Rm_{\rm min}$![]() and $S_{\rm min}$
and $S_{\rm min}$![]() have been collected for the minima of the curves in figures 1 and 2 which we shall call the critical values. Obviously, the influences of the boundary conditions are only small for the containers with large gaps. One finds the $Rm_{\rm min}$
have been collected for the minima of the curves in figures 1 and 2 which we shall call the critical values. Obviously, the influences of the boundary conditions are only small for the containers with large gaps. One finds the $Rm_{\rm min}$![]() with vacuum boundary condition as always smaller than for perfect-conductor conditions (except for very thin gaps) but the $S_{\rm min}$
with vacuum boundary condition as always smaller than for perfect-conductor conditions (except for very thin gaps) but the $S_{\rm min}$![]() are always larger. Consequently, the corresponding magnetic Mach numbers are much larger for cylinders made from perfect conductors. For such containers the axial wavenumbers are always larger than for insulating walls.
are always larger. Consequently, the corresponding magnetic Mach numbers are much larger for cylinders made from perfect conductors. For such containers the axial wavenumbers are always larger than for insulating walls.
With our normalizations the vertical extent $\delta z$![]() of one cell of the instability pattern, normalized by the gap width $D=R_{\rm out} - R_{\rm in}$
of one cell of the instability pattern, normalized by the gap width $D=R_{\rm out} - R_{\rm in}$![]() between the cylinders, is given by
between the cylinders, is given by
Flat cells are described by $\zeta <1$![]() while axially elongated cells possess $\zeta >1$
while axially elongated cells possess $\zeta >1$![]() . For $r_{{\rm in}}=0.5$
. For $r_{{\rm in}}=0.5$![]() it is simply $\zeta = {{\rm \pi} }/{ k}$
it is simply $\zeta = {{\rm \pi} }/{ k}$![]() so that for $k\simeq {\rm \pi}$
so that for $k\simeq {\rm \pi}$![]() the shape of the cell in the ($R$
the shape of the cell in the ($R$![]() –$z$
–$z$![]() ) plane is almost circular. The examples given in table 1, however, show that the wavenumbers do not reach the value of ${\rm \pi}$
) plane is almost circular. The examples given in table 1, however, show that the wavenumbers do not reach the value of ${\rm \pi}$![]() for medium $r_{{\rm in}}$
for medium $r_{{\rm in}}$![]() hence the cells are always elongated in the axial direction. This is true for models with both sorts of boundary conditions. For perfect-conducting cylinder walls $\zeta >1$
hence the cells are always elongated in the axial direction. This is true for models with both sorts of boundary conditions. For perfect-conducting cylinder walls $\zeta >1$![]() hardly varies with $r_{{\rm in}}$
hardly varies with $r_{{\rm in}}$![]() – the cells are always oblong. Evidently, such cells are not suitable to provide the angular momentum transport in accretion disks or galaxies.
– the cells are always oblong. Evidently, such cells are not suitable to provide the angular momentum transport in accretion disks or galaxies.
For perfect-conducting cylinders it follows that $\zeta \simeq 1.8$![]() for almost all $r_{{\rm in}}$
for almost all $r_{{\rm in}}$![]() , while it can become significantly larger for insulating material. The minimum axial extent of a container-probing MRI pattern is thus $H\simeq 1.8 D$
, while it can become significantly larger for insulating material. The minimum axial extent of a container-probing MRI pattern is thus $H\simeq 1.8 D$![]() . The aspect ratio $H/D$
. The aspect ratio $H/D$![]() of the Princeton experiment is 2.1. It happens that the numerical $\zeta$
of the Princeton experiment is 2.1. It happens that the numerical $\zeta$![]() -values differ by almost a factor of two for models with the same geometry but with different boundary conditions.
-values differ by almost a factor of two for models with the same geometry but with different boundary conditions.
4.2. Extremal gaps, thin-shell approximation
We note that for very wide gaps with $r_{{\rm in}}\simeq 0.1$![]() the characteristic Lundquist numbers $S_{\rm min}$
the characteristic Lundquist numbers $S_{\rm min}$![]() – for which the associated Reynolds number is minimal – are reduced to values of order unity while for very narrow gaps with $r_{{\rm in}}\simeq 0.95$
– for which the associated Reynolds number is minimal – are reduced to values of order unity while for very narrow gaps with $r_{{\rm in}}\simeq 0.95$![]() the Lundquist numbers are maximal. In both limits the Reynolds numbers $Rm_{\rm min}$
the Lundquist numbers are maximal. In both limits the Reynolds numbers $Rm_{\rm min}$![]() possess enlarged values. As also the linear dimension $R_0$
possess enlarged values. As also the linear dimension $R_0$![]() becomes small for small and/or large $r_{{\rm in}}$
becomes small for small and/or large $r_{{\rm in}}$![]() the necessary inner rotation rates become very large excluding the applicability of containers with very wide and/or very narrow gaps between the cylinders for experiments. One finds that containers with $0.3 \lesssim r_{{\rm in}} \lesssim 0.6$
the necessary inner rotation rates become very large excluding the applicability of containers with very wide and/or very narrow gaps between the cylinders for experiments. One finds that containers with $0.3 \lesssim r_{{\rm in}} \lesssim 0.6$![]() require the least rotation rates for excitation of standard magnetorotational instability. On the other hand, for both sorts of boundary conditions the models with $r_{{\rm in}} \simeq 0.2$
require the least rotation rates for excitation of standard magnetorotational instability. On the other hand, for both sorts of boundary conditions the models with $r_{{\rm in}} \simeq 0.2$![]() require the weakest magnetic fields.
require the weakest magnetic fields.
Table 1 also gives the results for very thin gaps between the cylinders up to $r_{{\rm in}}=0.95$![]() (Donnelly & Ozima Reference Donnelly and Ozima1960, Reference Donnelly and Ozima1962). The most striking difference due to the choice of the boundary conditions is here the numerical value of the calculated magnetic Mach number (last column). For $r_{{\rm in}}\to 1$
(Donnelly & Ozima Reference Donnelly and Ozima1960, Reference Donnelly and Ozima1962). The most striking difference due to the choice of the boundary conditions is here the numerical value of the calculated magnetic Mach number (last column). For $r_{{\rm in}}\to 1$![]() the characteristic Reynolds number grows to larger and larger values. We did not find a maximum of $Rm_{\rm min}$
the characteristic Reynolds number grows to larger and larger values. We did not find a maximum of $Rm_{\rm min}$![]() for $r_{{\rm in}}\to 1$
for $r_{{\rm in}}\to 1$![]() . As the $R_0^2$
. As the $R_0^2$![]() runs with $1-r_{{\rm in}}$
runs with $1-r_{{\rm in}}$![]() for $r_{{\rm in}}\to 1$
for $r_{{\rm in}}\to 1$![]() we find $\varOmega _{{\rm in}}\to \infty$
we find $\varOmega _{{\rm in}}\to \infty$![]() in this limit. It should thus not be possible to work with a thin-shell approximation (Edmonds Reference Edmonds1958) for numerical or experimental realizations of the standard MRI in TC flows.
in this limit. It should thus not be possible to work with a thin-shell approximation (Edmonds Reference Edmonds1958) for numerical or experimental realizations of the standard MRI in TC flows.
5. The non-axisymmetric modes
The excitation of non-axisymmetric modes requires faster rotation and stronger magnetic fields than the excitation of the axisymmetric modes (figures 1 and 2; dashed lines). For medium $r_{{\rm in}}$![]() of approximately 0.5 (red) the lines of marginal stability hardly depend on the radius of the inner cylinder. As also the geometric radius $R_0$
of approximately 0.5 (red) the lines of marginal stability hardly depend on the radius of the inner cylinder. As also the geometric radius $R_0$![]() is almost constant for different $r_{{\rm in}}$
is almost constant for different $r_{{\rm in}}$![]() the rotation frequencies and magnetic field amplitudes needed to excite non-axisymmetric modes are almost the same for such values of $r_{{\rm in}}$
the rotation frequencies and magnetic field amplitudes needed to excite non-axisymmetric modes are almost the same for such values of $r_{{\rm in}}$![]() . However, for wide gaps and for weak magnetic fields with $S< S_{\rm min}$
. However, for wide gaps and for weak magnetic fields with $S< S_{\rm min}$![]() the Reynolds numbers for excitation of the $m=1$
the Reynolds numbers for excitation of the $m=1$![]() modes are much higher than those for the excitation of the axisymmetric modes with $m=0$
modes are much higher than those for the excitation of the axisymmetric modes with $m=0$![]() . We note that the curves for the weak-field branch with $S< S_{\rm min}$
. We note that the curves for the weak-field branch with $S< S_{\rm min}$![]() become very steep so that the excitation of non-axisymmetric modes requires very rapid rotation.
become very steep so that the excitation of non-axisymmetric modes requires very rapid rotation.
For wide gaps between the cylinders ($r_{{\rm in}}=0.3$![]() , green) one finds that the lowest Reynolds number belongs to much higher Lundquist numbers than for $r_{{\rm in}}\simeq 0.5$
, green) one finds that the lowest Reynolds number belongs to much higher Lundquist numbers than for $r_{{\rm in}}\simeq 0.5$![]() . In addition, the curves for low Lundquist numbers are much steeper than the curve for the corresponding axisymmetric mode. Hence, for wide gaps with $r_{{\rm in}}\lesssim 0.4$
. In addition, the curves for low Lundquist numbers are much steeper than the curve for the corresponding axisymmetric mode. Hence, for wide gaps with $r_{{\rm in}}\lesssim 0.4$![]() it is almost impossible to excite the axisymmetric and the non-axisymmetric mode simultaneously by SMRI-experiments with Lundquist numbers not much higher than unity.
it is almost impossible to excite the axisymmetric and the non-axisymmetric mode simultaneously by SMRI-experiments with Lundquist numbers not much higher than unity.
The non-axisymmetric modes are drifting in the azimuthal direction. The drift rates, $\omega _{\rm dr}={\rm Re}(\omega )/\varOmega _{{\rm in}}$![]() , are given in figure 3. According to the relation
, are given in figure 3. According to the relation
the negative $\omega _{\rm dr}$![]() plotted in the figures indicate a migration of the patterns in the direction of the global rotation – for both sorts of boundary conditions. In all cases the azimuthal migration is faster than the rotation of the outer cylinder ($\omega _{\rm dr}>\mu$
plotted in the figures indicate a migration of the patterns in the direction of the global rotation – for both sorts of boundary conditions. In all cases the azimuthal migration is faster than the rotation of the outer cylinder ($\omega _{\rm dr}>\mu$![]() ).
).

Figure 3. Drift rates $\omega _{\rm dr}={\rm Re}(\omega )/\varOmega _{{\rm in}}$![]() of the non-axisymmetric modes $m=1$
of the non-axisymmetric modes $m=1$![]() (dashed lines): $r_{{\rm in}}=0.3$
(dashed lines): $r_{{\rm in}}=0.3$![]() (green); $r_{{\rm in}}=0.4$
(green); $r_{{\rm in}}=0.4$![]() , $r_{{\rm in}}=0.5$
, $r_{{\rm in}}=0.5$![]() (red); $r_{{\rm in}}=0.6$
(red); $r_{{\rm in}}=0.6$![]() . (a) Perfect-conducting cylinder material; (b) insulating cylinder material. Quasi-Keplerian differential rotation, $Pm=10^{-5}$
. (a) Perfect-conducting cylinder material; (b) insulating cylinder material. Quasi-Keplerian differential rotation, $Pm=10^{-5}$![]() .
.
6. Marginal stability for weak fields
It is possible to apply weak magnetic fields with $S< S_{\rm min}$![]() . Then, however, the Reynolds numbers necessary for excitation basically grow and the unstable wavenumbers become smaller, i.e. the cells become longer. Figure 4 demonstrates these weak-field solutions with $S< S_{\rm min}$
. Then, however, the Reynolds numbers necessary for excitation basically grow and the unstable wavenumbers become smaller, i.e. the cells become longer. Figure 4 demonstrates these weak-field solutions with $S< S_{\rm min}$![]() for $r_{{\rm in}}=0.3$
for $r_{{\rm in}}=0.3$![]() (figure 4a) and $r_{{\rm in}}=0.4$
(figure 4a) and $r_{{\rm in}}=0.4$![]() (figure 4b). The vertical lines represent the magnetic fields $B=2150$
(figure 4b). The vertical lines represent the magnetic fields $B=2150$![]() G (corresponding to $S=0.96$
G (corresponding to $S=0.96$![]() ) and $B=2750$
) and $B=2750$![]() G (corresponding to $S=1.22$
G (corresponding to $S=1.22$![]() ) reported for gallium SMRI experiments by Wang et al. (Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022b). We have also to note the influence of the boundary conditions: for insulating cylinders the curves for weak fields with $S< S_{\rm min}$
) reported for gallium SMRI experiments by Wang et al. (Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022b). We have also to note the influence of the boundary conditions: for insulating cylinders the curves for weak fields with $S< S_{\rm min}$![]() are so steep that the necessary critical Reynolds numbers at the vertical lines exceed the $Rm_{\rm min}$
are so steep that the necessary critical Reynolds numbers at the vertical lines exceed the $Rm_{\rm min}$![]() of the curves by more than one order of magnitude. This extreme enhancement is slightly reduced for perfect-conducting cylinder material but still the enhancement of the critical Reynolds number is by a factor of three relative to $Rm_{\rm min}$
of the curves by more than one order of magnitude. This extreme enhancement is slightly reduced for perfect-conducting cylinder material but still the enhancement of the critical Reynolds number is by a factor of three relative to $Rm_{\rm min}$![]() . This is even a minimum value as the real cylinders are, by far, not perfect-conducting. For galinstan as the fluid and stainless steel as the (outer) cylinder material the ratio
. This is even a minimum value as the real cylinders are, by far, not perfect-conducting. For galinstan as the fluid and stainless steel as the (outer) cylinder material the ratio
of the electric conductivities of the cylinders and the fluid is 0.47, which neither well approaches perfect-conduction nor vacuum boundary conditions. For sodium experiments one finds $\hat \sigma \simeq 0.16$![]() , hence the vacuum boundary conditions might provide the appropriate description. Rüdiger et al. (Reference Rüdiger, Schultz, Stefani and Hollerbach2018b) derived the form of the boundary conditions with finite values of (6.1) and have shown that for $\hat \sigma$
, hence the vacuum boundary conditions might provide the appropriate description. Rüdiger et al. (Reference Rüdiger, Schultz, Stefani and Hollerbach2018b) derived the form of the boundary conditions with finite values of (6.1) and have shown that for $\hat \sigma$![]() of order unity the resulting eigenvalues can approximately be interpolated between the values for $\hat \sigma =0$
of order unity the resulting eigenvalues can approximately be interpolated between the values for $\hat \sigma =0$![]() (insulating boundaries) and $\hat \sigma =\infty$
(insulating boundaries) and $\hat \sigma =\infty$![]() (perfect-conducting boundaries).
(perfect-conducting boundaries).

Figure 4. Stability lines of the axisymmetric modes for $r_{{\rm in}}=0.3$![]() (a) and $r_{{\rm in}}=0.4$
(a) and $r_{{\rm in}}=0.4$![]() (b) of containers with perfect-conducting cylinders (red) and with insulating cylinders (black). The lines of experiments with imperfectly conducting cylinders are located between the curves marked with ‘vac.’ and ‘cond.’. The vertical lines mark the Lundquist numbers after (2.15a,b) for the Princeton MRI-experiments represented by the lowest and the highest solid circles in their figure 2(a) (magnetic fields 2150 G and 2750 G) while the asterisks belong the used magnetic Reynolds numbers. With the planned Dresdyn sodium experiment the same magnetic field amplitudes will belong to Lundquist numbers exceeding 15.
(b) of containers with perfect-conducting cylinders (red) and with insulating cylinders (black). The lines of experiments with imperfectly conducting cylinders are located between the curves marked with ‘vac.’ and ‘cond.’. The vertical lines mark the Lundquist numbers after (2.15a,b) for the Princeton MRI-experiments represented by the lowest and the highest solid circles in their figure 2(a) (magnetic fields 2150 G and 2750 G) while the asterisks belong the used magnetic Reynolds numbers. With the planned Dresdyn sodium experiment the same magnetic field amplitudes will belong to Lundquist numbers exceeding 15.
Detailed consequences of the application of weak magnetic fields for the excitation of the axisymmetric mode are shown in figure 4. The Lundquist number (2.15a,b) is marked by vertical lines for a container with $R_{{\rm out}}=20.3$![]() cm, $r_{{\rm in}}=0.35$
cm, $r_{{\rm in}}=0.35$![]() filled with galinstan ($\rho =6.4$
filled with galinstan ($\rho =6.4$![]() g cm$^{-3}$
g cm$^{-3}$![]() and $\eta =2428$
and $\eta =2428$![]() cm$^2$
cm$^2$![]() s$^{-1}$
s$^{-1}$![]() ) with its magnetic Prandtl number of $1.4\times 10^{-6}$
) with its magnetic Prandtl number of $1.4\times 10^{-6}$![]() . The numbers correspond to the gallium experiment by Wang et al. (Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022b). The maximally possible uniform magnetic field in this experiment given as 4800 G corresponds to a Lundquist number after (2.15a,b) of $S=2.1$
. The numbers correspond to the gallium experiment by Wang et al. (Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022b). The maximally possible uniform magnetic field in this experiment given as 4800 G corresponds to a Lundquist number after (2.15a,b) of $S=2.1$![]() . One finds with figure 4 that for such fields the minimum magnetic Reynolds number for marginal stability must exceed 20, corresponding to a minimum value of 10.8 in the notation of Wang et al. (Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022b). The left vertical lines in figure 4 represent the reported MRI realization for Lehnert number $B_0=0.2$
. One finds with figure 4 that for such fields the minimum magnetic Reynolds number for marginal stability must exceed 20, corresponding to a minimum value of 10.8 in the notation of Wang et al. (Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022b). The left vertical lines in figure 4 represent the reported MRI realization for Lehnert number $B_0=0.2$![]() Footnote 1 and Reynolds number 3.4 (their notation, lower asterisk) provided by their figure 2(a). The experiment with the fastest rotation (upper asterisk) belongs to a Lundquist number of $S=1.22$
Footnote 1 and Reynolds number 3.4 (their notation, lower asterisk) provided by their figure 2(a). The experiment with the fastest rotation (upper asterisk) belongs to a Lundquist number of $S=1.22$![]() (right vertical lines).
(right vertical lines).
If the typical parameters of the experiment with almost Keplerian flow and with maximal Reynolds number are transformed to our definitions (2.15a,b), one obtains maximal Reynolds numbers of $Rm=8.4$![]() (right asterisks in the plots) which does not reach the values required for marginal instability at any Lundquist number. This deficit is particularly drastic for vacuum boundary conditions.
(right asterisks in the plots) which does not reach the values required for marginal instability at any Lundquist number. This deficit is particularly drastic for vacuum boundary conditions.
Because of the exceptional meaning of the Kepler rotation in astrophysics, all calculations have been performed for the rotation law with $q=1.5$![]() . The question may arise how relevant the results are for experiments with rotation laws somewhat steeper than the Keplerian one. The coefficient $q$
. The question may arise how relevant the results are for experiments with rotation laws somewhat steeper than the Keplerian one. The coefficient $q$![]() in the Princeton experiment is $q=1.59$
in the Princeton experiment is $q=1.59$![]() . As mentioned above, the same pair of $q$
. As mentioned above, the same pair of $q$![]() s yields $\mu =0.35$
s yields $\mu =0.35$![]() and $\mu =0.33$
and $\mu =0.33$![]() for $r_{{\rm in}}=0.5$
for $r_{{\rm in}}=0.5$![]() . For this case table 1 provides a magnetic Reynolds number of 24.7 for perfect-conducting boundaries. This is 14 % higher than the value 21.3 given in the Introduction for $\mu =0.33$
. For this case table 1 provides a magnetic Reynolds number of 24.7 for perfect-conducting boundaries. This is 14 % higher than the value 21.3 given in the Introduction for $\mu =0.33$![]() , representing the difference of the Reynolds numbers for Keplerian rotation with $q=1.5$
, representing the difference of the Reynolds numbers for Keplerian rotation with $q=1.5$![]() and for slightly super-Keplerian rotation with $q=1.59$
and for slightly super-Keplerian rotation with $q=1.59$![]() . For the latter one has thus to shift the curves in figure 4 downwards by (say) 14 %. The uncertainties due to the application of the too ideal boundary conditions, however, will overcompensate this small shift so that the stability line of the real experiment will certainly remain in the area between the limiting curves in figure 4.
. For the latter one has thus to shift the curves in figure 4 downwards by (say) 14 %. The uncertainties due to the application of the too ideal boundary conditions, however, will overcompensate this small shift so that the stability line of the real experiment will certainly remain in the area between the limiting curves in figure 4.
Our results comply with the finding of Goodman & Ji (Reference Goodman and Ji2002) in their figures 1 and 2, that containers with insulating walls of $r_{{\rm in}}=0.33$![]() including a quasi-Keplerian flow do not allow the excitation of SMRI with an applied field of less than 2750 G. Even with perfect-conducting cylinders the curves are so steep for $S< S_{\rm min}$
including a quasi-Keplerian flow do not allow the excitation of SMRI with an applied field of less than 2750 G. Even with perfect-conducting cylinders the curves are so steep for $S< S_{\rm min}$![]() that the needed rotation rates of the cylinders are too high.
that the needed rotation rates of the cylinders are too high.
7. Flat cells
As demonstrated by table 1 the cell structure for the axisymmetric modes is nearly circular in the $(R-z)$![]() -plane for wide gaps and rather elongated in the axial direction for narrow gaps. It is thus still unclear whether the standard MRI is also able to produce flat cells with $\zeta \ll 1$
-plane for wide gaps and rather elongated in the axial direction for narrow gaps. It is thus still unclear whether the standard MRI is also able to produce flat cells with $\zeta \ll 1$![]() which are necessary to appear in experiments with a flat container ($H< D$
which are necessary to appear in experiments with a flat container ($H< D$![]() ) and/or in flat cosmical objects such as accretion disks and galaxies. For the latter, the magnetic Mach number of rotation does not exceed values of 10, as it is the case for the solutions given in table 1.
) and/or in flat cosmical objects such as accretion disks and galaxies. For the latter, the magnetic Mach number of rotation does not exceed values of 10, as it is the case for the solutions given in table 1.
We have therefore to probe whether eigensolutions exist for finite $Rm$![]() and $S$
and $S$![]() when, for example, $\zeta =0.1$
when, for example, $\zeta =0.1$![]() is required. From (4.1) one obtains for (say) $r_{{\rm in}}=0.1$
is required. From (4.1) one obtains for (say) $r_{{\rm in}}=0.1$![]() that solutions with $k=10.5$
that solutions with $k=10.5$![]() are matched for $\zeta =0.1$
are matched for $\zeta =0.1$![]() .
.
Figure 5 shows the results. Indeed, the envisaged flat cells exist in the axially unbounded container and even for similar Lundquist numbers as for the solutions with the lowest Reynolds numbers and the elongated cells. The actual magnetic Reynolds numbers for flat cell structures, however, are much higher than before. Hence, the magnetic Mach numbers for flat cells are also higher than for the elongated cells summarized in table 1. They are larger than 10 and grow for growing flatness. This result complies with that of a global model of a flat galaxy for magnetic Prandtl number $Pm\geq 1$![]() (Kitchatinov & Rüdiger Reference Kitchatinov and Rüdiger2004). The flatter the cells, the stronger the dissipation and the harder the differential rotation must work to excite the instability while the magnetic field needed for the rotation minimum remains unchanged. We also learn from figure 5 that the influence of the actual boundary condition is remarkably weak.
(Kitchatinov & Rüdiger Reference Kitchatinov and Rüdiger2004). The flatter the cells, the stronger the dissipation and the harder the differential rotation must work to excite the instability while the magnetic field needed for the rotation minimum remains unchanged. We also learn from figure 5 that the influence of the actual boundary condition is remarkably weak.

Figure 5. Lines of marginal stability for $r_{{\rm in}}=0.1$![]() and a fixed axial wavenumber of $k=10.5$
and a fixed axial wavenumber of $k=10.5$![]() for $\zeta =0.1$
for $\zeta =0.1$![]() and $k=21$
and $k=21$![]() for $\zeta =0.05$
for $\zeta =0.05$![]() : perfect-conductingcylinders (red); insulating cylinders (black). The flatter the cell the higher the magnetic Mach number. The influence of the boundary conditions is rather weak; $m=0$
: perfect-conductingcylinders (red); insulating cylinders (black). The flatter the cell the higher the magnetic Mach number. The influence of the boundary conditions is rather weak; $m=0$![]() , quasi-Keplerian rotation, $Pm=10^{-5}$
, quasi-Keplerian rotation, $Pm=10^{-5}$![]() .
.
8. Discussion
The influence of the position $r_{{\rm in}}$![]() of the inner cylinder of TC flows on the excitation of the magnetorotational instability has been studied. To demonstrate the results we shall switch to the more traditional representations
of the inner cylinder of TC flows on the excitation of the magnetorotational instability has been studied. To demonstrate the results we shall switch to the more traditional representations
(where simply the $r_{{\rm in}}$![]() -dependent $R_0$
-dependent $R_0$![]() in the parameters (2.15a,b) has been replaced by the fixed $R_{{\rm out}}$
in the parameters (2.15a,b) has been replaced by the fixed $R_{{\rm out}}$![]() ) which for given outer cylinder size $R_{{\rm out}}$
) which for given outer cylinder size $R_{{\rm out}}$![]() form minimal normalized inner rotation rates and magnetic field amplitudes needed for excitation of the instability. These quantities are plotted as function of $r_{{\rm in}}$
form minimal normalized inner rotation rates and magnetic field amplitudes needed for excitation of the instability. These quantities are plotted as function of $r_{{\rm in}}$![]() in figure 6 for both sorts of boundary conditions. The main result is that too narrow or too wide gaps would require very high rotation rates or very strong magnetic fields. For $0.3\lesssim r_{{\rm in}} \lesssim 0.6$
in figure 6 for both sorts of boundary conditions. The main result is that too narrow or too wide gaps would require very high rotation rates or very strong magnetic fields. For $0.3\lesssim r_{{\rm in}} \lesssim 0.6$![]() the dependence of the numbers on $r_{{\rm in}}$
the dependence of the numbers on $r_{{\rm in}}$![]() is rather weak. The minima for conducting cylinders are at $r_{{\rm in}}\simeq 0.4$
is rather weak. The minima for conducting cylinders are at $r_{{\rm in}}\simeq 0.4$![]() for the rotation rate and at $r_{{\rm in}}\simeq 0.2$
for the rotation rate and at $r_{{\rm in}}\simeq 0.2$![]() for the magnetic field. We also note that the influence of the boundary conditions is opposite for rotation and field. For vacuum conditions the needed rotation rates are mostly lower than for perfect-conduction conditions but the needed magnetic fields are higher for insulating cylinders.
for the magnetic field. We also note that the influence of the boundary conditions is opposite for rotation and field. For vacuum conditions the needed rotation rates are mostly lower than for perfect-conduction conditions but the needed magnetic fields are higher for insulating cylinders.

Figure 6. The magnetic Reynolds number (a) and the Lundquist number (b) after the definitions (8.1a,b) representing the normalized inner rotation rate and the magnetic field amplitude needed for excitation versus $r_{{\rm in}}$![]() . Quasi-Keplerian differential rotation, $Pm=10^{-5}$
. Quasi-Keplerian differential rotation, $Pm=10^{-5}$![]() , perfect-conducting cylinder material (red), insulating cylinders (black). The numbers are taken from table 1.
, perfect-conducting cylinder material (red), insulating cylinders (black). The numbers are taken from table 1.
One may ask whether for given outer radius not only the inner rotation frequency has a minimum for a certain $r_{{\rm in}}$![]() but also the momentum to maintain this critical $\varOmega _{{\rm in}}$
but also the momentum to maintain this critical $\varOmega _{{\rm in}}$![]() . To this end one has to multiply $Rm^*$
. To this end one has to multiply $Rm^*$![]() from figure 6(a) with $r_{{\rm in}}^2$
from figure 6(a) with $r_{{\rm in}}^2$![]() . The result is a monotonously increasing function for $r_{{\rm in}}\geq 0.1$
. The result is a monotonously increasing function for $r_{{\rm in}}\geq 0.1$![]() . In this range there is no minimum at any $r_{{\rm in}}$
. In this range there is no minimum at any $r_{{\rm in}}$![]() for the power to drive the inner cylinder. Such a minimum could maximally exist very close to the axis which, however, is not relevant for real constructions.
for the power to drive the inner cylinder. Such a minimum could maximally exist very close to the axis which, however, is not relevant for real constructions.
The experiment with the fastest rotation ($Rm=4.5$![]() ) by Wang et al. (Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022b) corresponds to $Rm^*=37$
) by Wang et al. (Reference Wang, Gilson, Ebrahimi, Goodman and Ji2022b) corresponds to $Rm^*=37$![]() which is certainly below the curves in figure 6(a). A similar situation holds with respect to the magnetic field: the given maximal possible field of 4800 G provides a Lundquist number of $S^*=4.4$
which is certainly below the curves in figure 6(a). A similar situation holds with respect to the magnetic field: the given maximal possible field of 4800 G provides a Lundquist number of $S^*=4.4$![]() which again does not reach the minimum value in figure 6(b). Compared with our calculations the reported experiments are clearly subcritical with respect to the magnetic field and the reported rotation rates. There is no value of $r_{{\rm in}}$
which again does not reach the minimum value in figure 6(b). Compared with our calculations the reported experiments are clearly subcritical with respect to the magnetic field and the reported rotation rates. There is no value of $r_{{\rm in}}$![]() for which the applied rotation rates and/or magnetic fields are supercritical by a large margin. If TC experiments which are subcritical in the described sense provide unstable modes then extra influences (such as electric currents, non-zonal flows or non-axial field components) besides homogeneous axial magnetic background fields and differential rotation as the standard combination of SMRI should be active. Nonlinear simulations of axially unbounded SMRI models with medium magnetic Prandtl numbers never did provide instability patterns if for given Lundquist number the applied Reynolds number is lower than the minimum Reynolds number taken from the linear theory (Rüdiger et al. Reference Rüdiger, Gellert, Hollerbach, Schultz and Stefani2018a). For an interpretation of the observed axisymmetric and even non-axisymmetric instabilities (see Wang et al. Reference Wang, Gilson, Ebrahimi, Goodman, Caspary, Winarto and Ji2022a) the specific role of the Ekman–Hartmann layers inside the copper lids indeed leading to subcritical instability excitations should be discussed (Gilman & Benton Reference Gilman and Benton1968; Szklarski & Rüdiger Reference Szklarski and Rüdiger2007; Gissinger, Goodman & Ji Reference Gissinger, Goodman and Ji2012) but this is not the task of this paper.
for which the applied rotation rates and/or magnetic fields are supercritical by a large margin. If TC experiments which are subcritical in the described sense provide unstable modes then extra influences (such as electric currents, non-zonal flows or non-axial field components) besides homogeneous axial magnetic background fields and differential rotation as the standard combination of SMRI should be active. Nonlinear simulations of axially unbounded SMRI models with medium magnetic Prandtl numbers never did provide instability patterns if for given Lundquist number the applied Reynolds number is lower than the minimum Reynolds number taken from the linear theory (Rüdiger et al. Reference Rüdiger, Gellert, Hollerbach, Schultz and Stefani2018a). For an interpretation of the observed axisymmetric and even non-axisymmetric instabilities (see Wang et al. Reference Wang, Gilson, Ebrahimi, Goodman, Caspary, Winarto and Ji2022a) the specific role of the Ekman–Hartmann layers inside the copper lids indeed leading to subcritical instability excitations should be discussed (Gilman & Benton Reference Gilman and Benton1968; Szklarski & Rüdiger Reference Szklarski and Rüdiger2007; Gissinger, Goodman & Ji Reference Gissinger, Goodman and Ji2012) but this is not the task of this paper.
Acknowledgements
F. Stefani (Dresden-Rossendorf) is acknowledged for discussions of the presented problem and a critical reading of the manuscript. This research received no specific grant from any funding agency, commercial or not-for-profit sectors. The authors report no conflict of interest.
Editor S. Tobias thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.