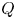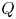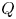1 Introduction
The Elsässer variables (Elsasser Reference Elsasser1950) are expressed as
where $\boldsymbol {V}$![]() is the speed of the plasma and $\boldsymbol {V}_{A}=\boldsymbol {B}/\sqrt{\mu \rho}$
is the speed of the plasma and $\boldsymbol {V}_{A}=\boldsymbol {B}/\sqrt{\mu \rho}$![]() is the vectorial Alfvén speed expressed in terms of the magnetic field $\boldsymbol {B}$
is the vectorial Alfvén speed expressed in terms of the magnetic field $\boldsymbol {B}$![]() , density $\rho$
, density $\rho$![]() and magnetic permeability $\mu$
and magnetic permeability $\mu$![]() . In magnetohydrodynamics (MHD), these Elsässer variables play a unique role, which conveniently corresponds to Alfvén waves. A single Alfvén wave may be expressed through a single Elsässer variable.
. In magnetohydrodynamics (MHD), these Elsässer variables play a unique role, which conveniently corresponds to Alfvén waves. A single Alfvén wave may be expressed through a single Elsässer variable.
Because of this convenient property and the prevalence of Alfvén wave turbulence in the solar wind, the Elsässer variables have been used numerous times in the description of the plasma in the solar wind (e.g. Dobrowolny, Mangeney & Veltri Reference Dobrowolny, Mangeney and Veltri1980; Marsch & Tu Reference Marsch and Tu1989; Tu, Marsch & Thieme Reference Tu, Marsch and Thieme1989; Velli, Grappin & Mangeney Reference Velli, Grappin and Mangeney1989; Zhou & Matthaeus Reference Zhou and Matthaeus1989; Grappin, Mangeney & Marsch Reference Grappin, Mangeney and Marsch1990; Bruno & Carbone Reference Bruno and Carbone2013). With the Elsässer variables, it is straightforward to show that Alfvén wave turbulence exists because of the interaction of counterpropagating Alfvén waves (Bruno & Carbone Reference Bruno and Carbone2013) in incompressible MHD. Given the great success of the Elsässer variables, Marsch & Mangeney (Reference Marsch and Mangeney1987) have even gone so far as to rewrite the entire set of MHD equations in terms of the independent variables, comprising the Elsässer variables and the density. In that paper, it is clear that the entire machinery of MHD waves can be recovered for this set of equations in terms of Elsässer variables and density. This set of equations offers the possibility to study the evolution of MHD waves through the Elsässer variables. The caveat is that the Elsässer variables are really only well suited to model Alfvén waves.
However, for other waves, the Elsässer variables are less well suited, because other MHD waves necessarily consist of a combination of both Elsässer variables. For example, Magyar, Van Doorsselaere & Goossens (Reference Magyar, Van Doorsselaere and Goossens2019a) show that this is particularly true for slow and fast magnetosonic waves in a homogeneous plasma. But this statement also holds for most waves in a non-uniform plasma. Ismayilli et al. (Reference Ismayilli, Van Doorsselaere, Goossens and Magyar2022) calculated the Elsässer variables for surface Alfvén waves on a discontinuous interface between two homogeneous plasmas, and clearly show that both Elsässer components are non-zero for this surface Alfvén wave. Moreover, the Elsässer variables are no longer uniquely associated with upward or downward propagation. For instance, an upward-propagating kink wave in a cylindrical plasma has both Elsässer variables co-propagating along the magnetic field (Van Doorsselaere et al. Reference Van Doorsselaere, Li, Goossens, Hnat and Magyar2020). Their continuous interaction would lead to an efficient formation of turbulence, and this turbulence from a unidirectional transverse wave is called uniturbulence (Magyar, Van Doorsselaere & Goossens Reference Magyar, Van Doorsselaere and Goossens2017). To study the nonlinear evolution of such waves in inhomogeneous plasmas, a more general approach than Elsässer variables is needed.
In direct measurements in the solar wind, it has been found many times that the magnetic field fluctuations and the velocity fluctuations are highly correlated, showing that they are highly Alfvénic (Bavassano & Bruno Reference Bavassano and Bruno2000). This is expressed through the Alfvén ratio $r_{A}$![]() , which is the ratio of the kinetic energy and the magnetic energy, which is found to be close to 1 close to the Sun. However, it has also been found in solar wind data that the slope of the correlation between the magnetic field fluctuations and the velocity fluctuations is not always 1 (Marsch & Tu Reference Marsch and Tu1993). This is potentially because of the presence of other wave modes than Alfvén waves. Thus, also observationally, there is a need for a generalisation of the Elsässer variables.
, which is the ratio of the kinetic energy and the magnetic energy, which is found to be close to 1 close to the Sun. However, it has also been found in solar wind data that the slope of the correlation between the magnetic field fluctuations and the velocity fluctuations is not always 1 (Marsch & Tu Reference Marsch and Tu1993). This is potentially because of the presence of other wave modes than Alfvén waves. Thus, also observationally, there is a need for a generalisation of the Elsässer variables.
Here, we consider a generalisation of the Elsässer variables by considering them as co-moving with the wave, using the phase speed as a parameter. We call these the $Q$![]() -variables. However, the push for a generalisation of Elsässer variables is embraced in the wider community. For example, Galtier (Reference Galtier2023) has considered so-called canonical variables. With these canonical variables, he described successfully the interaction and cascade of fast mode waves. Thus, it seems that more general Elsässer variables are possible, and this should be a research question that is actively pursued, given the tremendous impact of the Elsässer variables.
-variables. However, the push for a generalisation of Elsässer variables is embraced in the wider community. For example, Galtier (Reference Galtier2023) has considered so-called canonical variables. With these canonical variables, he described successfully the interaction and cascade of fast mode waves. Thus, it seems that more general Elsässer variables are possible, and this should be a research question that is actively pursued, given the tremendous impact of the Elsässer variables.
2 Results
2.1 The MHD equations written in terms of $Q$ -variables
-variables
In what follows, we introduce a new parameter $\alpha$![]() , which describes the wave phase speed, for a general wave. We then introduce the $Q$
, which describes the wave phase speed, for a general wave. We then introduce the $Q$![]() -variables by
-variables by
where it is clear that the limit $\alpha =1/\sqrt {\mu \rho }$![]() recovers the special case of Elsässer variables. Taking this limit thus always allows us to check our equations against the relevant equations in Marsch & Mangeney (Reference Marsch and Mangeney1987).
recovers the special case of Elsässer variables. Taking this limit thus always allows us to check our equations against the relevant equations in Marsch & Mangeney (Reference Marsch and Mangeney1987).
We start from the same set of ideal MHD equations as Marsch & Mangeney (Reference Marsch and Mangeney1987) do. They read
where the total pressure is defined as $P_{T}=p+\frac {1}{2}\rho V_{A}^2$![]() , using the gas pressure $p$
, using the gas pressure $p$![]() and vectorial Alfvén speed $\boldsymbol {V}_{A}=\boldsymbol {B}/\sqrt {\mu \rho }$
and vectorial Alfvén speed $\boldsymbol {V}_{A}=\boldsymbol {B}/\sqrt {\mu \rho }$![]() . They are complimented with an adiabatic assumption for the energy equation
. They are complimented with an adiabatic assumption for the energy equation
where $\gamma$![]() is the adiabatic exponent.
is the adiabatic exponent.
2.1.1 Solenoidal constraint
Let us first consider the solenoidal constraint (2.5). We rewrite it in terms of $Q$![]() -variables, through the expression of $\boldsymbol {B}$
-variables, through the expression of $\boldsymbol {B}$![]() in terms of $\boldsymbol {Q}^\pm$
in terms of $\boldsymbol {Q}^\pm$![]()
Inserting that into (2.5) allows us to write
or, after simplification,
Considering the limiting case of $\alpha ^2=1/\mu \rho, \boldsymbol {Q}^\pm =\boldsymbol {Z}^\pm, \boldsymbol {Z}^+-\boldsymbol {Z}^-=\boldsymbol {V}_{A}$![]() , we recover equation (10) of Marsch & Mangeney (Reference Marsch and Mangeney1987).
, we recover equation (10) of Marsch & Mangeney (Reference Marsch and Mangeney1987).
2.1.2 Conservation of mass
Next, we rewrite the conservation of mass (2.3). We use it for finding an expression for $({{\rm D}^\pm }/{{\rm D} t})(\ln {\rho })$![]() , where ${\rm D}^\pm /{\rm D} t=\partial /\partial t+\boldsymbol {Q}^\pm \boldsymbol {\cdot }\boldsymbol {\nabla }$
, where ${\rm D}^\pm /{\rm D} t=\partial /\partial t+\boldsymbol {Q}^\pm \boldsymbol {\cdot }\boldsymbol {\nabla }$![]() is the derivative co-moving with the wave, in the so-called waveframe. We find
is the derivative co-moving with the wave, in the so-called waveframe. We find
where the continuity equation (2.3) was used in the last equation. To this last equation, we add on the right-hand side ($\mp \times$![]() (2.9)) to find
(2.9)) to find
where we have used the expressions for $\boldsymbol {V}$![]() in terms of $\boldsymbol {Q}^\pm$
in terms of $\boldsymbol {Q}^\pm$![]() in the equations
in the equations
When the limit of $\alpha ^2\to 1/\sqrt {\mu \rho }$![]() is considered, the last term of (2.14) cancels out and (16) of Marsch & Mangeney (Reference Marsch and Mangeney1987) is readily recovered.
is considered, the last term of (2.14) cancels out and (16) of Marsch & Mangeney (Reference Marsch and Mangeney1987) is readily recovered.
2.1.3 Momentum equation
Now we turn to the momentum equation and the induction equation, (2.2) and (2.4), which form the key equation (17) of Marsch & Mangeney (Reference Marsch and Mangeney1987). Following their lead, we add (2.2)$\pm \alpha$![]() (2.4). In the first step, we use the expansion of $\boldsymbol {Q}^\mp \boldsymbol {\cdot }\boldsymbol {\nabla }\boldsymbol {Q}^\pm$
(2.4). In the first step, we use the expansion of $\boldsymbol {Q}^\mp \boldsymbol {\cdot }\boldsymbol {\nabla }\boldsymbol {Q}^\pm$![]() as
as
where we have used the vector identity $\boldsymbol {C}\boldsymbol {\cdot }\boldsymbol {\nabla }(\,f\boldsymbol {D})=f\boldsymbol {C}\boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {D}+\boldsymbol {D}(\boldsymbol {C}\boldsymbol {\cdot }\boldsymbol {\nabla } f)$![]() for any vector fields $\boldsymbol {C}$
for any vector fields $\boldsymbol {C}$![]() and $\boldsymbol {D}$
and $\boldsymbol {D}$![]() and scalar field $f$
and scalar field $f$![]() . We also define the parameter
. We also define the parameter
The $\Delta \alpha ^2$![]() parameter expresses how far a wave's phase speed is from the Alfvén speed. Since a wave can be slower or faster than the Alfvén speed, the $\Delta \alpha ^2$
parameter expresses how far a wave's phase speed is from the Alfvén speed. Since a wave can be slower or faster than the Alfvén speed, the $\Delta \alpha ^2$![]() parameter may be positive or negative, despite the square! The square in the notation is kept for dimensional purposes to keep $\Delta \alpha$
parameter may be positive or negative, despite the square! The square in the notation is kept for dimensional purposes to keep $\Delta \alpha$![]() in the same units as $\alpha$
in the same units as $\alpha$![]() . In the limit of $\alpha ={1}/{\sqrt {\mu \rho }}$
. In the limit of $\alpha ={1}/{\sqrt {\mu \rho }}$![]() , the parameter $\Delta \alpha ^2$
, the parameter $\Delta \alpha ^2$![]() will turn to 0: $\Delta \alpha ^2=0$
will turn to 0: $\Delta \alpha ^2=0$![]() and $\boldsymbol {Q}^\pm =\boldsymbol {Z}^\pm$
and $\boldsymbol {Q}^\pm =\boldsymbol {Z}^\pm$![]() turns into the classical Elsässer variable. Here, it is also useful to point out that it will be convenient to use expressions with $\rho \alpha ^2$
turns into the classical Elsässer variable. Here, it is also useful to point out that it will be convenient to use expressions with $\rho \alpha ^2$![]() , which are constant in this limit.
, which are constant in this limit.
With the above expressions, we obtain from (2.2)$\pm \alpha$![]() (2.4) the result
(2.4) the result
The first two terms on the right-hand side group with the left-hand side to form the co-moving derivative
We now find an expression for the terms on the right-hand side. For the total pressure term, we find


where we have used the adiabatic relationship of $p(\rho )$![]() which introduces the expression for the sound speed $v_{s}=\sqrt {{\gamma p}/{\rho }}$
which introduces the expression for the sound speed $v_{s}=\sqrt {{\gamma p}/{\rho }}$![]() .
.
The second term on the right-hand side of (2.19) can be rewritten with the expression for $\boldsymbol {B}$![]() in terms of $\boldsymbol {Q}^\pm$
in terms of $\boldsymbol {Q}^\pm$![]() as
as

The third term on the right-hand side of (2.19) should be handled through the modified version of the continuity relation (2.13). From that equation, we have that

Substituting everything in (2.19), we now have

After moving the right-hand side convective derivative to the left-hand side and subsequently adding (${\pm } ({(\boldsymbol {Q}^+-\boldsymbol {Q}^-)}/{4})\times$![]() (2.14)) and using (2.9), we obtain the final result
(2.14)) and using (2.9), we obtain the final result

Taking the limit of $\alpha =\sqrt {1/\mu \rho }$![]() allows us to confirm that this equation converges in that case to equation (17) of Marsch & Mangeney (Reference Marsch and Mangeney1987). The last term on the left-hand side and the last three terms on the right-hand side are terms parallel to the magnetic field. We remind the reader that these equations are valid for any choice of $\alpha$
allows us to confirm that this equation converges in that case to equation (17) of Marsch & Mangeney (Reference Marsch and Mangeney1987). The last term on the left-hand side and the last three terms on the right-hand side are terms parallel to the magnetic field. We remind the reader that these equations are valid for any choice of $\alpha$![]() (satisfying basic dimensional arguments).
(satisfying basic dimensional arguments).
2.2 Linearised $Q$ -equations
-equations
In a first attempt to better understand the $Q$![]() -variables and the role that $\alpha$
-variables and the role that $\alpha$![]() plays in the MHD equations, we shall linearise the MHD equations (2.9), (2.14), (2.26) around a uniform equilibrium. We take $\rho =\rho _0+\delta \rho, \boldsymbol {B}=B_0\boldsymbol {e_z}+\boldsymbol {\delta B}, \boldsymbol {V}=\boldsymbol {V_0}+\boldsymbol {\delta V}, \boldsymbol {Q}^\pm =\boldsymbol {Q}_0^\pm +\boldsymbol {\delta Q}^\pm$
plays in the MHD equations, we shall linearise the MHD equations (2.9), (2.14), (2.26) around a uniform equilibrium. We take $\rho =\rho _0+\delta \rho, \boldsymbol {B}=B_0\boldsymbol {e_z}+\boldsymbol {\delta B}, \boldsymbol {V}=\boldsymbol {V_0}+\boldsymbol {\delta V}, \boldsymbol {Q}^\pm =\boldsymbol {Q}_0^\pm +\boldsymbol {\delta Q}^\pm$![]() , where quantities with subscript 0 are constant equilibrium quantities, and $\delta$
, where quantities with subscript 0 are constant equilibrium quantities, and $\delta$![]() indicates Eulerian perturbations (where we have used the Chandrasekhar notation for such). The Cartesian coordinate system $(x,y,z)$
indicates Eulerian perturbations (where we have used the Chandrasekhar notation for such). The Cartesian coordinate system $(x,y,z)$![]() is aligned with the magnetic field in the $z$
is aligned with the magnetic field in the $z$![]() -direction. We have not linearised $\alpha$
-direction. We have not linearised $\alpha$![]() , because we shall show later that it is proportional to the phase speed of the wave. Moreover, a linearisation of $\alpha$
, because we shall show later that it is proportional to the phase speed of the wave. Moreover, a linearisation of $\alpha$![]() would result in terms rewritten from $\delta \rho$
would result in terms rewritten from $\delta \rho$![]() and other physical parameters, and consequently the equation for the linearised $\alpha$
and other physical parameters, and consequently the equation for the linearised $\alpha$![]() would be linearly dependent on the previous equations.
would be linearly dependent on the previous equations.
Adopting a similar notation as Marsch & Mangeney (Reference Marsch and Mangeney1987), we have
We have utilised that the background variables are uniform, and that $\alpha$![]() does not need to be linearised. We have also rejected any terms higher than the first order in perturbations and defined the quantity $\delta R$
does not need to be linearised. We have also rejected any terms higher than the first order in perturbations and defined the quantity $\delta R$![]() . Additionally we linearise the co-moving advective derivative $D^\pm /Dt$
. Additionally we linearise the co-moving advective derivative $D^\pm /Dt$![]() as
as
where the notation of Marsch & Mangeney (Reference Marsch and Mangeney1987) was once again used to define ${\rm d}^\pm /{\rm d} t$![]() . Note also that the last term always results in 0 when operating on equilibrium quantities, given their assumed homogeneity. Action of the last term on linear quantities results in a second-order contribution, which is neglected. With this notation, the MHD equations are rewritten as
. Note also that the last term always results in 0 when operating on equilibrium quantities, given their assumed homogeneity. Action of the last term on linear quantities results in a second-order contribution, which is neglected. With this notation, the MHD equations are rewritten as

Given the homogeneity, the linear wave solutions may be written with the plane wave notation $\exp {({\rm i}\boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {x}-{\rm i}\omega t)}$![]() , where we choose the $x$
, where we choose the $x$![]() -axis to be in the $\boldsymbol {k}-\boldsymbol {B}_0$
-axis to be in the $\boldsymbol {k}-\boldsymbol {B}_0$![]() -plane resulting in $k_y\equiv 0$
-plane resulting in $k_y\equiv 0$![]() . For the plane waves, the co-moving derivative is rewritten as ${\rm d}^\pm /{\rm d} t=-{\rm i}(\omega - \boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {Q}^\pm _0)\equiv -{\rm i}\omega ^\pm$
. For the plane waves, the co-moving derivative is rewritten as ${\rm d}^\pm /{\rm d} t=-{\rm i}(\omega - \boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {Q}^\pm _0)\equiv -{\rm i}\omega ^\pm$![]() , where we have yet again used the notation of Marsch & Mangeney (Reference Marsch and Mangeney1987). With these notations, we can split the $Q$
, where we have yet again used the notation of Marsch & Mangeney (Reference Marsch and Mangeney1987). With these notations, we can split the $Q$![]() -equations (2.30)–(2.31) into its components
-equations (2.30)–(2.31) into its components


which form a system of 7 equations for 7 unknowns. It has eigenvalue $\omega$![]() . Remember, in these equations, $\alpha$
. Remember, in these equations, $\alpha$![]() can still be chosen freely!
can still be chosen freely!
2.2.1 Alfvén waves
As expected, the $y$![]() -component (2.35) is separated from the other equations. This equation is rewritten in the following system:
-component (2.35) is separated from the other equations. This equation is rewritten in the following system:
resulting in a dispersion relation
with solutions

which nicely converges to the well-known Alfvén wave solution $\omega =\boldsymbol {k}\boldsymbol {\cdot }(\boldsymbol {V}_0\pm \boldsymbol {V}_{A})=\boldsymbol {k}\boldsymbol {\cdot } \boldsymbol {Z}^\pm _0$![]() .
.
This subsection also points us in the direction of the meaning and importance of the $\alpha$![]() parameter. If we would change variables to the co-moving frame (co-moving with $\boldsymbol {Q}^\pm _0$
parameter. If we would change variables to the co-moving frame (co-moving with $\boldsymbol {Q}^\pm _0$![]() ), then that frame would require that either $\omega ^\pm =0$
), then that frame would require that either $\omega ^\pm =0$![]() separately. Implementing these conditions in (2.37) and (2.38), leads to the (single) condition
separately. Implementing these conditions in (2.37) and (2.38), leads to the (single) condition
From this condition, we obtain that $(\delta Q^+_y-\delta Q^-_y)\equiv 0$![]() or that $\Delta \alpha ^2\equiv 0$
or that $\Delta \alpha ^2\equiv 0$![]() . The former condition would lead to $\delta Q^\pm _y\equiv 0$
. The former condition would lead to $\delta Q^\pm _y\equiv 0$![]() through the companion equation (e.g. (2.38) for $\omega ^-=0$
through the companion equation (e.g. (2.38) for $\omega ^-=0$![]() ), which tells us that there is no physical solution with non-zero amplitude. The latter condition $\Delta \alpha ^2=0$
), which tells us that there is no physical solution with non-zero amplitude. The latter condition $\Delta \alpha ^2=0$![]() leads to the well-known solution $\alpha ^2=1/\mu \rho _0$
leads to the well-known solution $\alpha ^2=1/\mu \rho _0$![]() , which is equivalent to the limit where the $Q$
, which is equivalent to the limit where the $Q$![]() -variables coincide with the Elsässer variables. This thus shows that the Elsässer variables are the only co-propagating waveframe variables in which the Alfvén waves have a non-zero amplitude. It shows that $\alpha$
-variables coincide with the Elsässer variables. This thus shows that the Elsässer variables are the only co-propagating waveframe variables in which the Alfvén waves have a non-zero amplitude. It shows that $\alpha$![]() should be chosen according to the phase speed, through the solution of $\omega ^\pm =0$
should be chosen according to the phase speed, through the solution of $\omega ^\pm =0$![]()
resulting in an expression for $\alpha$![]()
The reader is cautioned to be careful with this expression, given that the expression diverges if $k\to 0$![]() or perpendicular $\boldsymbol {k}$
or perpendicular $\boldsymbol {k}$![]() and $\boldsymbol {B}_0$
and $\boldsymbol {B}_0$![]() .
.
2.2.2 Magnetoacoustic waves
Let us now investigate magnetoacoustic waves as they appear in terms of $Q$![]() -variables. For the specific geometry chosen without loss of generality in § 2.2, linear magnetoacoustic modes perturb the $Q$
-variables. For the specific geometry chosen without loss of generality in § 2.2, linear magnetoacoustic modes perturb the $Q$![]() -variables in the $x$
-variables in the $x$![]() –$z$
–$z$![]() plane, and density. The system of equations to be solved for magnetoacoustic modes is composed of (2.33)–(2.36), except 2.35, which were treated in the previous subsection, yielding Alfvén waves. The dispersion relation is given by the determinant of this system of 5 equations for 5 unknowns. However, it turns out that, in this system, there are only 4 independent equations, (2.33) being linearly dependent on the other equations. Instead, we use the linearised solenoidal constraint (2.32) as a fifth equation
plane, and density. The system of equations to be solved for magnetoacoustic modes is composed of (2.33)–(2.36), except 2.35, which were treated in the previous subsection, yielding Alfvén waves. The dispersion relation is given by the determinant of this system of 5 equations for 5 unknowns. However, it turns out that, in this system, there are only 4 independent equations, (2.33) being linearly dependent on the other equations. Instead, we use the linearised solenoidal constraint (2.32) as a fifth equation
Next, we use the standard dispersion relation of magnetosonic waves. Assuming that $|k| = 1$![]() , so that $k_z = \cos (\theta )$
, so that $k_z = \cos (\theta )$![]() and $k_x = \sin (\theta )$
and $k_x = \sin (\theta )$![]() , with $\theta$
, with $\theta$![]() being the angle between the background magnetic field $B_0\boldsymbol {e}_z$
being the angle between the background magnetic field $B_0\boldsymbol {e}_z$![]() and the wavevector $\boldsymbol {k}$
and the wavevector $\boldsymbol {k}$![]() , and that there are no background flows $V_0 = 0$
, and that there are no background flows $V_0 = 0$![]() , the dispersion relation is
, the dispersion relation is
Note that we have not yet assumed any form for $\alpha$![]() , which is not needed for isolating the magnetoacoustic solutions. If we assume a form for $\alpha$
, which is not needed for isolating the magnetoacoustic solutions. If we assume a form for $\alpha$![]() like in (2.46), we recover the fifth, trivial, solution of the dispersion relation, $\omega = 0$
like in (2.46), we recover the fifth, trivial, solution of the dispersion relation, $\omega = 0$![]() , the entropy wave, which represents non-propagating perturbations of plasma density and temperature. The other four solutions are the up- and downward-propagating (with respect to $\boldsymbol {e}_z$
, the entropy wave, which represents non-propagating perturbations of plasma density and temperature. The other four solutions are the up- and downward-propagating (with respect to $\boldsymbol {e}_z$![]() ) fast and slow magnetoacoustic modes, as found also elsewhere through e.g. the velocity representation of MHD (Goedbloed & Poedts Reference Goedbloed and Poedts2004)
) fast and slow magnetoacoustic modes, as found also elsewhere through e.g. the velocity representation of MHD (Goedbloed & Poedts Reference Goedbloed and Poedts2004)

Here, we have 4 solutions with the symbol $\pm _{{\rm ud}}$![]() differentiating between upward- and downward-propagating waves, and the symbol $\pm _{{\rm sf}}$
differentiating between upward- and downward-propagating waves, and the symbol $\pm _{{\rm sf}}$![]() is the usual differentiation between the slow and fast magnetoacoustic waves. Recovering the magnetoacoustic solutions demonstrates the validity of the formulation of compressible MHD equations in terms of the $Q$
is the usual differentiation between the slow and fast magnetoacoustic waves. Recovering the magnetoacoustic solutions demonstrates the validity of the formulation of compressible MHD equations in terms of the $Q$![]() -variables.
-variables.
Using the eigenvalues in terms of $\omega$![]() (2.49), the eigenfunctions for $\boldsymbol {Q^\pm }$
(2.49), the eigenfunctions for $\boldsymbol {Q^\pm }$![]() can be determined for fast and slow waves from (2.30)–(2.32). The $Q$
can be determined for fast and slow waves from (2.30)–(2.32). The $Q$![]() -variables can also be computed directly from the velocity and magnetic field eigenfunctions, if we assume a form for $\alpha$
-variables can also be computed directly from the velocity and magnetic field eigenfunctions, if we assume a form for $\alpha$![]() . Note that the definition of $\alpha$
. Note that the definition of $\alpha$![]() from (2.46) diverges for purely perpendicularly propagating ($k_z = 0$
from (2.46) diverges for purely perpendicularly propagating ($k_z = 0$![]() ) fast waves, thus this definition is not suitable for fast waves. This uncovers a curious property of (2.33)–(2.36), in that advection (in the form of the co-moving advective derivative) is only explicitly present along the magnetic field, leaving the definition of the phase speed in $\alpha$
) fast waves, thus this definition is not suitable for fast waves. This uncovers a curious property of (2.33)–(2.36), in that advection (in the form of the co-moving advective derivative) is only explicitly present along the magnetic field, leaving the definition of the phase speed in $\alpha$![]() only in terms of $k_z$
only in terms of $k_z$![]() . A straightforward remedy is then to use the full magnitude of the wavevector instead of only the $k_z$
. A straightforward remedy is then to use the full magnitude of the wavevector instead of only the $k_z$![]() component in the definition of $\alpha = \omega k^{-1} B_0^{-1}$
component in the definition of $\alpha = \omega k^{-1} B_0^{-1}$![]() .
.
In figure 1 we represent the parallel and perpendicular eigenfunctions of the $Q$![]() -variables for fast and slow waves. From this figure, it is clear that only the perpendicular components are separated as a function of propagation direction with respect to the background magnetic field. In other words, $Q^+_{s,f \perp }$
-variables for fast and slow waves. From this figure, it is clear that only the perpendicular components are separated as a function of propagation direction with respect to the background magnetic field. In other words, $Q^+_{s,f \perp }$![]() is non-zero only when $\boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {B_0} > 0$
is non-zero only when $\boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {B_0} > 0$![]() , and $Q^-_{s,f \perp }$
, and $Q^-_{s,f \perp }$![]() is non-zero for $\boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {B_0} < 0$
is non-zero for $\boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {B_0} < 0$![]() . The parallel components $Q^\pm _{s,f \parallel }$
. The parallel components $Q^\pm _{s,f \parallel }$![]() are generally both perturbed, thus, based on the present form of the $Q$
are generally both perturbed, thus, based on the present form of the $Q$![]() -variables, parallel perturbations cannot be separated into parallel- and anti-parallel-propagating components. The parallel components $Q^\pm _{s,f \parallel }$
-variables, parallel perturbations cannot be separated into parallel- and anti-parallel-propagating components. The parallel components $Q^\pm _{s,f \parallel }$![]() vanish only for purely parallel-propagating fast waves, which are just Alfvén waves polarised in plane. In the next section (§ 2.2.3), we show that this is because of the connection of $Q_\parallel$
vanish only for purely parallel-propagating fast waves, which are just Alfvén waves polarised in plane. In the next section (§ 2.2.3), we show that this is because of the connection of $Q_\parallel$![]() to the magnetic pressure.
to the magnetic pressure.

Figure 1. Polar plots representing the $\theta$![]() -dependence of the magnitude of the parallel (a) and perpendicular (b) $Q^\pm$
-dependence of the magnitude of the parallel (a) and perpendicular (b) $Q^\pm$![]() -variables, for both fast and slow waves, indicated with the subscripts $f$
-variables, for both fast and slow waves, indicated with the subscripts $f$![]() and $s$
and $s$![]() , respectively. The magnitudes are normalised by multiplying with the phase speed $\omega _{s,f}/|k|$
, respectively. The magnitudes are normalised by multiplying with the phase speed $\omega _{s,f}/|k|$![]() where $|k| = 1.$
where $|k| = 1.$![]() Here, the plasma-$\beta$
Here, the plasma-$\beta$![]() is set to 0.2.
is set to 0.2.
We conjecture that the full separation of waves, including the component parallel to the background field, is possible by constructing a waveframe variable which includes the total pressure or density perturbation as well in its formulation, but this will solely work in a homogeneous plasma where such a neat separation is possible.
2.2.3 Kink waves
In order to model kink waves, we start from (2.30)–(2.31), written out in components. Once again, we use the same frame of reference: the magnetic field $\boldsymbol {B}_0$![]() is pointing in the $z$
is pointing in the $z$![]() -direction, and we also take the flow in the $z$
-direction, and we also take the flow in the $z$![]() -direction $\boldsymbol {V}_0=V_0\boldsymbol {e_z}$
-direction $\boldsymbol {V}_0=V_0\boldsymbol {e_z}$![]() . Additionally, we take the assumption of a pressureless plasma $v_{s}=0$
. Additionally, we take the assumption of a pressureless plasma $v_{s}=0$![]() and we take a density step function at $x=0$
and we take a density step function at $x=0$![]() , with a constant density $\rho _{L}$
, with a constant density $\rho _{L}$![]() ($\rho _{R}$
($\rho _{R}$![]() ) on the left (right) side of the interface. In each half-space, the waves may be Fourier analysed in $y$
) on the left (right) side of the interface. In each half-space, the waves may be Fourier analysed in $y$![]() , $z$
, $z$![]() and $t$
and $t$![]() , putting every quantity proportional to $\exp {({\rm i}k_z z-{\rm i}\omega t)}$
, putting every quantity proportional to $\exp {({\rm i}k_z z-{\rm i}\omega t)}$![]() , where we have once again considered $k_y\equiv 0$
, where we have once again considered $k_y\equiv 0$![]() as in § 2.2. The resulting equations will be just like (2.33)–(2.36), except that the terms with $k_x$
as in § 2.2. The resulting equations will be just like (2.33)–(2.36), except that the terms with $k_x$![]() will be replaced by a derivative ${\rm d}/{{\rm d}x}$
will be replaced by a derivative ${\rm d}/{{\rm d}x}$![]() . In what follows, we ignore (2.35), because we will not concentrate on the Alfvén waves, but rather on the kink waves, which are solely polarised in the $x,z$
. In what follows, we ignore (2.35), because we will not concentrate on the Alfvén waves, but rather on the kink waves, which are solely polarised in the $x,z$![]() -directions for $k_y=0$
-directions for $k_y=0$![]() .
.
Following the earlier strategy, we take (e.g.) $\omega ^+_{L,R}=0$![]() to find the upward-propagating kink waves. This immediately implies a connection
to find the upward-propagating kink waves. This immediately implies a connection
between $\alpha _{R,L}$![]() . Each quantity in this equation is the corresponding background quantity in the left half-space or right half-space, respectively, for subscripts $L$
. Each quantity in this equation is the corresponding background quantity in the left half-space or right half-space, respectively, for subscripts $L$![]() and $R$
and $R$![]() . With this assumption, we then have the following set of equations:
. With this assumption, we then have the following set of equations:




in which all quantities are subscripted with $R$![]() and $L$
and $L$![]() , respectively, for each half-space. Combining (2.53) and (2.52) isolates $\delta Q_x^+$
, respectively, for each half-space. Combining (2.53) and (2.52) isolates $\delta Q_x^+$![]() as
as
showing that the kink wave is uniquely described by $\delta Q_x^-$![]() only, because $\delta Q_x^+$
only, because $\delta Q_x^+$![]() is 0 if $k_z\neq 0$
is 0 if $k_z\neq 0$![]() and $B_0\neq 0$
and $B_0\neq 0$![]() . If we find a value for $\alpha _{R,L}$
. If we find a value for $\alpha _{R,L}$![]() and $\omega$
and $\omega$![]() , then the kink wave is written with only one of $\delta Q_x^\pm$
, then the kink wave is written with only one of $\delta Q_x^\pm$![]() , as was the intention of the $Q$
, as was the intention of the $Q$![]() -variables for separating upward- and downward-propagating waves. Similarly, from the combination of (2.54) and (2.55) (and using $\delta Q_x^+=0$
-variables for separating upward- and downward-propagating waves. Similarly, from the combination of (2.54) and (2.55) (and using $\delta Q_x^+=0$![]() ), we obtain
), we obtain
Thus, we obtain a set of equations describing the kink waves (or any other wave under these assumptions) from (2.52) and (2.57)
Introducing a new variable $\varPi =\delta Q^+_z-\delta Q^-_z$![]() , we obtain the set
, we obtain the set
This set is reminiscent of the coupled differential equations between the perturbed total pressure and displacement that other works have found for the description of kink waves (Appert, Gruber & Vaclavik Reference Appert, Gruber and Vaclavik1974; Goossens, Hollweg & Sakurai Reference Goossens, Hollweg and Sakurai1992; Ismayilli et al. Reference Ismayilli, Van Doorsselaere, Goossens and Magyar2022), which have a strong correspondence to the currently modelled surface Alfvén waves (Goossens et al. Reference Goossens, Andries, Soler, Van Doorsselaere, Arregui and Terradas2012).
Since each quantity is constant in each half-space, we can substitute one of the equations in the other. Then, we obtain a single second-order differential equation
In the left and right half-spaces, we consider respectively the solution
where
The solution for $\varPi$![]() can be calculated from (2.60).
can be calculated from (2.60).
Next, we need to apply boundary conditions at $x=0$![]() . Namely, we take (as usual)
. Namely, we take (as usual)
where $P'=B_0b_z/\mu$![]() is the perturbed total pressure and the square brackets are differences between the left and the right of the interface. Note that the extra term in the Lagrangian pressure perturbation is 0 in the linear regime, since the magnetic pressure is uniform in each half-space. Translated to our variables, these boundary conditions are
is the perturbed total pressure and the square brackets are differences between the left and the right of the interface. Note that the extra term in the Lagrangian pressure perturbation is 0 in the linear regime, since the magnetic pressure is uniform in each half-space. Translated to our variables, these boundary conditions are
The first condition states that $A_{L}=A_{R}$![]() , while the second condition results in the dispersion relation
, while the second condition results in the dispersion relation
Squaring this relation, and inserting the expression for $\kappa ^2=k_z^2|\mu \rho \alpha ^2-1|$![]() , we obtain
, we obtain
where we have used the fact that the absolute values in $\kappa ^2$![]() take a different sign on either side of the interface. Solving this equation in conjunction with (2.50) (and considering $V_0=0$
take a different sign on either side of the interface. Solving this equation in conjunction with (2.50) (and considering $V_0=0$![]() for simplicity), we obtain finally the allowed values for $\alpha$
for simplicity), we obtain finally the allowed values for $\alpha$![]()

Given that $B_{L}=B_{R}=B_0$![]() for a pressureless plasma, these equations reduce to
for a pressureless plasma, these equations reduce to

as is well known from other works.
2.2.4 General waves in field-aligned flows
Now we will prove explicitly that the proper choice of $\alpha$![]() splits the $Q$
splits the $Q$![]() -variable between wave modes of propagation directions. We follow the derivation of Magyar, Van Doorsselaere & Goossens (Reference Magyar, Van Doorsselaere and Goossens2019b) and their equation (19). In this subsection, we consider the general configuration with a magnetic field pointing in the $z$
-variable between wave modes of propagation directions. We follow the derivation of Magyar, Van Doorsselaere & Goossens (Reference Magyar, Van Doorsselaere and Goossens2019b) and their equation (19). In this subsection, we consider the general configuration with a magnetic field pointing in the $z$![]() -direction, but still dependent on $x$
-direction, but still dependent on $x$![]() and $y$
and $y$![]() . Moreover, we also take the background flow along the magnetic field
. Moreover, we also take the background flow along the magnetic field
Let us now consider the linearised induction equation
of which we will only consider the perpendicular component. We can reduce this induction equation with vector identities to
Here, we have naturally used that $\boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {B}_0=\boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {b}=0$![]() , but we have also used $\boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {V}_0=0$
, but we have also used $\boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {V}_0=0$![]() because $\boldsymbol {V}_0$
because $\boldsymbol {V}_0$![]() only has a $z$
only has a $z$![]() -component that does not depend on $z$
-component that does not depend on $z$![]() . Using Fourier analysis for the ignorable coordinates $z$
. Using Fourier analysis for the ignorable coordinates $z$![]() and $t$
and $t$![]() , we then have
, we then have
Using (2.7) and (2.15), we then have
This equation shows that the correct choice of $\alpha$![]() indeed splits a wave mode with a specific $\omega$
indeed splits a wave mode with a specific $\omega$![]() and $k_z$
and $k_z$![]() between different $\boldsymbol {\delta Q}_\perp$
between different $\boldsymbol {\delta Q}_\perp$![]() components. Using the $Q$
components. Using the $Q$![]() -variable terminology, the equation is more elegantly written as
-variable terminology, the equation is more elegantly written as
This equation states that a wave with phase speed $\boldsymbol {Q}_0^\pm$![]() has the associated wave only present in $\boldsymbol {\delta Q}_\perp ^\mp$
has the associated wave only present in $\boldsymbol {\delta Q}_\perp ^\mp$![]() , with the other $Q$
, with the other $Q$![]() -variable $\boldsymbol {\delta Q}_\perp ^\pm =0$
-variable $\boldsymbol {\delta Q}_\perp ^\pm =0$![]() .
.
2.3 Splitting the equations for different wave modes
The linearised $Q$![]() -equations (2.30)–(2.31) and their component versions (2.33)–(2.36) show that the operator on the right-hand side of these equations is a linear operator, and yields a vector proportional to its input plane wave solution with dependence $\exp {({\rm i}\boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {x}-{\rm i}\omega t)}$
-equations (2.30)–(2.31) and their component versions (2.33)–(2.36) show that the operator on the right-hand side of these equations is a linear operator, and yields a vector proportional to its input plane wave solution with dependence $\exp {({\rm i}\boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {x}-{\rm i}\omega t)}$![]() . Moreover, we understand that the wave vector $\boldsymbol {k}$
. Moreover, we understand that the wave vector $\boldsymbol {k}$![]() and $\omega$
and $\omega$![]() must satisfy the dispersion relation.
must satisfy the dispersion relation.
In a future work, we want to construct models for the solar atmosphere, which are driven by different wave modes. In our upcoming models, we want to take a step back from the linear approach, and once again use the full operator. The plan is to use a WKB approach (after Wentzel–Kramers–Brillouin) as detailed in Marsch & Tu (Reference Marsch and Tu1989), Tu & Marsch (Reference Tu and Marsch1993) and van der Holst et al. (Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014). Such a model with only Alfvén wave drivers is called an AWSOM (Alfvén wave driven solar model) (van der Holst et al. Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014). We want to extend this model by also including the kink waves, their self-interaction and damping, leading to a model named UAWSOM (uniturbulence and Alfvén wave driven solar model). Thus we are looking forward to taking
where $\boldsymbol {Q}_0^\pm$![]() stands for the slowly varying background, $\boldsymbol {\delta Q}^\pm _{k}$
stands for the slowly varying background, $\boldsymbol {\delta Q}^\pm _{k}$![]() is the contribution of the (respectively up- and downward-propagating) kink waves and $\boldsymbol {\delta Q}^\pm _{A}$
is the contribution of the (respectively up- and downward-propagating) kink waves and $\boldsymbol {\delta Q}^\pm _{A}$![]() the contribution from the (up- and downward) Alfvén waves, as classically used in AWSOM type models (Evans et al. Reference Evans, Opher, Oran, van der Holst, Sokolov, Frazin, Gombosi and Vásquez2012; van der Holst et al. Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014; Réville et al. Reference Réville, Velli, Panasenco, Tenerani, Shi, Badman, Bale, Kasper, Stevens and Korreck2020). In the employed WKB approximation, we consider a background $\boldsymbol {Q}_0^\pm$
the contribution from the (up- and downward) Alfvén waves, as classically used in AWSOM type models (Evans et al. Reference Evans, Opher, Oran, van der Holst, Sokolov, Frazin, Gombosi and Vásquez2012; van der Holst et al. Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014; Réville et al. Reference Réville, Velli, Panasenco, Tenerani, Shi, Badman, Bale, Kasper, Stevens and Korreck2020). In the employed WKB approximation, we consider a background $\boldsymbol {Q}_0^\pm$![]() slowly varying along $\boldsymbol {B}_0$
slowly varying along $\boldsymbol {B}_0$![]() and in time. We thus consider the dominant Fourier components of $\boldsymbol {Q}_0^\pm$
and in time. We thus consider the dominant Fourier components of $\boldsymbol {Q}_0^\pm$![]() to be with wavelengths (or scale heights, if you wish) much larger than the wavelengths of the kink and Alfvén waves, and periods (or time scales of variation, if you like) much larger than the periods of the kink and Alfvén waves.
to be with wavelengths (or scale heights, if you wish) much larger than the wavelengths of the kink and Alfvén waves, and periods (or time scales of variation, if you like) much larger than the periods of the kink and Alfvén waves.
Let us first only consider the linearised version of (2.26) and (2.14), and call its associated operator $\mathcal {L}_\alpha$![]() acting on the eigenvector to be $\mathcal {U}$
acting on the eigenvector to be $\mathcal {U}$![]() (consisting of $\boldsymbol {Q}^\pm$
(consisting of $\boldsymbol {Q}^\pm$![]() and $\rho$
and $\rho$![]() )
)
We realise that the linear operators on the left-hand side and right-hand side will just split out over the different contributions $\boldsymbol {\delta Q}^\pm _{k}$![]() and $\boldsymbol {\delta Q}^\pm _{A}$
and $\boldsymbol {\delta Q}^\pm _{A}$![]() , because of the linear character of the operators. Each term for the kink wave in the equation will have a dependence $\exp {({\rm i} k_{z,{k}}z-{\rm i}\omega _{k} t)}$
, because of the linear character of the operators. Each term for the kink wave in the equation will have a dependence $\exp {({\rm i} k_{z,{k}}z-{\rm i}\omega _{k} t)}$![]() , and likewise the terms for the Alfvén waves will have a dependence of $\exp {({\rm i}k_{z,{A}}z-{\rm i}\omega _{A} t)}$
, and likewise the terms for the Alfvén waves will have a dependence of $\exp {({\rm i}k_{z,{A}}z-{\rm i}\omega _{A} t)}$![]() , where the pairs $(\omega _{k}, k_{z,{k}})$
, where the pairs $(\omega _{k}, k_{z,{k}})$![]() and $(\omega _{A}, k_{z,{A}})$
and $(\omega _{A}, k_{z,{A}})$![]() satisfy their respective dispersion relation for a (different!) driving frequency $\omega _{k}$
satisfy their respective dispersion relation for a (different!) driving frequency $\omega _{k}$![]() or $\omega _{A}$
or $\omega _{A}$![]() that finds its origin in the photospheric convective motions or p-modes (Morton, Weberg & McLaughlin Reference Morton, Weberg and McLaughlin2019). By using a Fourier transform of the linearised $Q$
that finds its origin in the photospheric convective motions or p-modes (Morton, Weberg & McLaughlin Reference Morton, Weberg and McLaughlin2019). By using a Fourier transform of the linearised $Q$![]() -equations, we then obtain a separated set of equations for each contribution
-equations, we then obtain a separated set of equations for each contribution
Here, the last equation for the equilibrium is in the WKB approximation an integration of the Fourier components $\omega$![]() smaller than the smallest wave frequency
smaller than the smallest wave frequency
which thus represents the slow evolution of the background. It is irrelevant for this last equation for the equilibrium which $\alpha$![]() value is chosen or used, because the equations are more conveniently written in terms of the classical MHD variables.
value is chosen or used, because the equations are more conveniently written in terms of the classical MHD variables.
The key point to realise in (2.81)–(2.82) is that they are still valid for any possible $\alpha$![]() that you prefer. Moreover, they are clearly independent, and thus $\alpha$
that you prefer. Moreover, they are clearly independent, and thus $\alpha$![]() may be chosen freely for both separately! Thus, for (2.82), we use the choice of $\alpha =1/\sqrt {\mu \rho }$
may be chosen freely for both separately! Thus, for (2.82), we use the choice of $\alpha =1/\sqrt {\mu \rho }$![]() reverting to the classical equation of van der Holst et al. (Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014). However, for the kink waves (2.81), we make the choice of the appropriate $\alpha$
reverting to the classical equation of van der Holst et al. (Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014). However, for the kink waves (2.81), we make the choice of the appropriate $\alpha$![]() , as found in (2.72). That then allows us to formulate the appropriate equations for upward- and downward-propagating kink waves, separating out their contributions.
, as found in (2.72). That then allows us to formulate the appropriate equations for upward- and downward-propagating kink waves, separating out their contributions.
If we assume that the nonlinearity and field-aligned inhomogeneity are sufficiently weak, we can consider the re-inclusion of the nonlinear terms in (2.26) and (2.14). They will be of the form $\boldsymbol {\delta Q}^\pm _{k} \boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {\delta Q}^\pm _{k}$![]() and $\boldsymbol {\delta Q}^\pm _{A} \boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {\delta Q}^\mp _{A}$
and $\boldsymbol {\delta Q}^\pm _{A} \boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {\delta Q}^\mp _{A}$![]() , and also include cross-terms between $\boldsymbol {\delta Q}_{A}$
, and also include cross-terms between $\boldsymbol {\delta Q}_{A}$![]() and $\boldsymbol {\delta Q}_{k}$
and $\boldsymbol {\delta Q}_{k}$![]() . Using the same Fourier argument as before, we should realise that the cross-terms will make no net contribution to the equations (2.81)–(2.82) when integrated over a longer time (this seems, however, in contradiction with the numerical experiments of Guo et al. Reference Guo, Van Doorsselaere, Karampelas, Li, Antolin and De Moortel2019). The other terms will contain the classical interaction of counterpropagating waves in Alfvén wave turbulence (Iroshnikov Reference Iroshnikov1964; Kraichnan Reference Kraichnan1967), acting as a net sink in the equations (2.81)–(2.82), but added as a source term in the equilibrium equations as in Marsch & Tu (Reference Marsch and Tu1989), Tu & Marsch (Reference Tu and Marsch1993), Evans et al. (Reference Evans, Opher, Oran, van der Holst, Sokolov, Frazin, Gombosi and Vásquez2012), van der Holst et al. (Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014) and Réville et al. (Reference Réville, Velli, Panasenco, Tenerani, Shi, Badman, Bale, Kasper, Stevens and Korreck2020). The terms in $\boldsymbol {\delta Q}^\pm _{k} \boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {\delta Q}^\pm _{k}$
. Using the same Fourier argument as before, we should realise that the cross-terms will make no net contribution to the equations (2.81)–(2.82) when integrated over a longer time (this seems, however, in contradiction with the numerical experiments of Guo et al. Reference Guo, Van Doorsselaere, Karampelas, Li, Antolin and De Moortel2019). The other terms will contain the classical interaction of counterpropagating waves in Alfvén wave turbulence (Iroshnikov Reference Iroshnikov1964; Kraichnan Reference Kraichnan1967), acting as a net sink in the equations (2.81)–(2.82), but added as a source term in the equilibrium equations as in Marsch & Tu (Reference Marsch and Tu1989), Tu & Marsch (Reference Tu and Marsch1993), Evans et al. (Reference Evans, Opher, Oran, van der Holst, Sokolov, Frazin, Gombosi and Vásquez2012), van der Holst et al. (Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014) and Réville et al. (Reference Réville, Velli, Panasenco, Tenerani, Shi, Badman, Bale, Kasper, Stevens and Korreck2020). The terms in $\boldsymbol {\delta Q}^\pm _{k} \boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {\delta Q}^\pm _{k}$![]() model the damping of the kink wave due to uniturbulence (Magyar et al. Reference Magyar, Van Doorsselaere and Goossens2017, Reference Magyar, Van Doorsselaere and Goossens2019b) due to its self-deformation. In Van Doorsselaere et al. (Reference Van Doorsselaere, Li, Goossens, Hnat and Magyar2020) it was found that this term also leads to a net contribution when averaged over longer times, similar to the Alfvén wave cascade. This extra contribution also acts as a sink in the kink wave evolution equation (2.81), and is added as an extra heating and pressure term in background MHD equations, just like the Alfvén wave cascade in the AWSOM model.
model the damping of the kink wave due to uniturbulence (Magyar et al. Reference Magyar, Van Doorsselaere and Goossens2017, Reference Magyar, Van Doorsselaere and Goossens2019b) due to its self-deformation. In Van Doorsselaere et al. (Reference Van Doorsselaere, Li, Goossens, Hnat and Magyar2020) it was found that this term also leads to a net contribution when averaged over longer times, similar to the Alfvén wave cascade. This extra contribution also acts as a sink in the kink wave evolution equation (2.81), and is added as an extra heating and pressure term in background MHD equations, just like the Alfvén wave cascade in the AWSOM model.
3 Conclusions
In this paper, we have started from the success of the Elsässer variables in describing and separating upward- and downward-propagating Alfvén waves. With the earlier realisation that any other wave than an Alfvén wave necessarily has both Elsässer components (Magyar et al. Reference Magyar, Van Doorsselaere and Goossens2019b), we have realised that the Elsässer variables need generalisation to other waves as well.
To fill this need, we have proposed the $Q$![]() -variables given by
-variables given by
with a parameter $\alpha$![]() that we have proven to be proportional to the phase speed of the wave. The value of $\alpha$
that we have proven to be proportional to the phase speed of the wave. The value of $\alpha$![]() is dependent on the type of wave and equilibrium parameters through the dispersion relation. We have rewritten the MHD equations in these $Q$
is dependent on the type of wave and equilibrium parameters through the dispersion relation. We have rewritten the MHD equations in these $Q$![]() -variables, following the lead of Marsch & Mangeney (Reference Marsch and Mangeney1987).
-variables, following the lead of Marsch & Mangeney (Reference Marsch and Mangeney1987).
In the next section of the paper, we have shown that (i) the modelling of Alfvén waves reverts back to the classical Elsässer variables, (ii) that slow and fast waves have also the perpendicular component of $\boldsymbol {Q}^\pm$![]() split between upward- and downward-propagating waves and (iii) that surface Alfvén waves in a non-uniform plasma can also be described by the $Q$
split between upward- and downward-propagating waves and (iii) that surface Alfvén waves in a non-uniform plasma can also be described by the $Q$![]() -variables, separating out upward- and downward-propagating waves. This shows that the generalisation of the Elsässer variables, as we set out to do, has been successful. Indeed, going beyond the Elsässer description, with the current $Q$
-variables, separating out upward- and downward-propagating waves. This shows that the generalisation of the Elsässer variables, as we set out to do, has been successful. Indeed, going beyond the Elsässer description, with the current $Q$![]() -variables, we can separate upward- and downward-propagating waves of many different types, including waves in inhomogeneous plasmas.
-variables, we can separate upward- and downward-propagating waves of many different types, including waves in inhomogeneous plasmas.
The significance of these $Q$![]() -variables is in enabling a more general approach to the Alfvén wave driven solar wind models (e.g. van der Holst et al. Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014). These models encapsulate in a one-dimensional way the additional heating by Alfvén waves (see Cranmer et al. (Reference Cranmer, Asgari-Targhi, Miralles, Raymond, Strachan, Tian and Woolsey2015), for a review). Thanks to this new development of the $Q$
-variables is in enabling a more general approach to the Alfvén wave driven solar wind models (e.g. van der Holst et al. Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014). These models encapsulate in a one-dimensional way the additional heating by Alfvén waves (see Cranmer et al. (Reference Cranmer, Asgari-Targhi, Miralles, Raymond, Strachan, Tian and Woolsey2015), for a review). Thanks to this new development of the $Q$![]() -variables, it will be possible to construct new solar wind models that also include wave driving by other wave modes. In particular, we have laid the mathematical groundwork for the creation of the UAWSOM model, which also incorporates the propagation of kink waves on inhomogeneous structures, such as plumes. Kink waves have been ubiquitously observed in the solar corona (Tomczyk et al. Reference Tomczyk, McIntosh, Keil, Judge, Schad, Seeley and Edmondson2007; Nechaeva et al. Reference Nechaeva, Zimovets, Nakariakov and Goddard2019) and possibly deliver significant energy input in coronal loops (Lim et al. Reference Lim, Van Doorsselaere, Berghmans, Morton, Pant and Mandal2023) and plumes (Thurgood, Morton & McLaughlin Reference Thurgood, Morton and McLaughlin2014). These kink waves self-interact nonlinearly and show uniturbulence (Magyar et al. Reference Magyar, Van Doorsselaere and Goossens2019b). This potentially leads to extra heating in the solar wind model, possibly resolving current shortcomings of the AWSOM model which underperforms in open field regions (Verdini et al. Reference Verdini, Velli, Matthaeus, Oughton and Dmitruk2010; van der Holst et al. Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2016, Reference van Ballegooijen and Asgari-Targhi2017; Verdini, Grappin & Montagud-Camps Reference Verdini, Grappin and Montagud-Camps2019). This potential extra heating by kink waves will be the subject of a future publication, in which we will derive the governing equations for the UAWSOM model, based on the current $Q$
-variables, it will be possible to construct new solar wind models that also include wave driving by other wave modes. In particular, we have laid the mathematical groundwork for the creation of the UAWSOM model, which also incorporates the propagation of kink waves on inhomogeneous structures, such as plumes. Kink waves have been ubiquitously observed in the solar corona (Tomczyk et al. Reference Tomczyk, McIntosh, Keil, Judge, Schad, Seeley and Edmondson2007; Nechaeva et al. Reference Nechaeva, Zimovets, Nakariakov and Goddard2019) and possibly deliver significant energy input in coronal loops (Lim et al. Reference Lim, Van Doorsselaere, Berghmans, Morton, Pant and Mandal2023) and plumes (Thurgood, Morton & McLaughlin Reference Thurgood, Morton and McLaughlin2014). These kink waves self-interact nonlinearly and show uniturbulence (Magyar et al. Reference Magyar, Van Doorsselaere and Goossens2019b). This potentially leads to extra heating in the solar wind model, possibly resolving current shortcomings of the AWSOM model which underperforms in open field regions (Verdini et al. Reference Verdini, Velli, Matthaeus, Oughton and Dmitruk2010; van der Holst et al. Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2016, Reference van Ballegooijen and Asgari-Targhi2017; Verdini, Grappin & Montagud-Camps Reference Verdini, Grappin and Montagud-Camps2019). This potential extra heating by kink waves will be the subject of a future publication, in which we will derive the governing equations for the UAWSOM model, based on the current $Q$![]() -variables. These will incorporate the evolution equations of the wave energy density. Moreover, but more speculatively, this formalism could be useful in deriving the effect of the parametric instability on the solar wind driving with Alfvén waves (Shoda et al. Reference Shoda, Suzuki, Asgari-Targhi and Yokoyama2019).
-variables. These will incorporate the evolution equations of the wave energy density. Moreover, but more speculatively, this formalism could be useful in deriving the effect of the parametric instability on the solar wind driving with Alfvén waves (Shoda et al. Reference Shoda, Suzuki, Asgari-Targhi and Yokoyama2019).
Furthermore, the adoption of these new $Q$![]() -variables allows the exploration of Solar Orbiter or Parker Solar Probe data, in regimes which are not highly Alfvénic. In particular, data series of low Alfvénicity could be re-analysed with the $Q$
-variables allows the exploration of Solar Orbiter or Parker Solar Probe data, in regimes which are not highly Alfvénic. In particular, data series of low Alfvénicity could be re-analysed with the $Q$![]() -variables to expose other wave modes in these regimes.
-variables to expose other wave modes in these regimes.
Acknowledgements
This research was supported by the International Space Science Institute (ISSI) in Bern, through ISSI International Team project #560: ‘Turbulence at the Edge of the Solar Corona: Constraining Available Theories Using the Latest Parker Solar Probe Measurements’.
Editor Steve Tobias thanks the referees for their advice in evaluating this article.
Funding
T.V.D. was supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No 724326), the C1 grant TRACEspace of Internal Funds KU Leuven and a Senior Research Project (G088021N) of the FWO Vlaanderen. Furthermore, T.V.D. received financial support from the Flemish Government under the long-term structural Methusalem funding program, project SOUL: Stellar evolution in full glory, grant METH/24/012 at KU Leuven. N.M. acknowledges Research Foundation – Flanders (FWO Vlaanderen) for their support through a Postdoctoral Fellowship. M.V.S. acknowledges support from the French Research Agency grant ANR STORMGENESIS #ANR-22-CE31-0013-01.
Declaration of interests
The authors report no conflict of interest.
Author contributions
TVD derived the theory, NM made the numerical solutions, all contributed to discussions during the research, all contributed to writing and editing the manuscript.