No CrossRef data available.
Published online by Cambridge University Press: 11 January 2024
Beam–target reactions in fusion plasmas play an important role in both magnetic confinement fusion and inertial confinement fusion in the condition of low-density plasmas with high-velocity interactions. The traditional method for calculating beam–target reaction rate neglects the transport process of incident particles in inhomogeneous plasmas, leading to errors providing that the temperature and density in the transport path of incident particles vary obviously. An improved method considering the transport process is proposed in this paper to eliminate the deficiencies. Then the method is employed in high-speed plasma collision studies. When the initial plasma density and temperature are set to $0.5\,{\rm g}\,{\rm cm}^{-3}$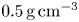 and 100 eV, it is found that the beam–target reaction rate calculated by the traditional method is almost identical to that by our method if the collision velocity is less than 600 km s$^{-1}$
and 100 eV, it is found that the beam–target reaction rate calculated by the traditional method is almost identical to that by our method if the collision velocity is less than 600 km s$^{-1}$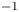 . However, the traditional method is not suitable for study as the collision velocity gets higher, inducing obvious differences, which can reach 70 % at 1000 km s$^{-1}$
. However, the traditional method is not suitable for study as the collision velocity gets higher, inducing obvious differences, which can reach 70 % at 1000 km s$^{-1}$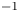 . The improved method will make large corrections to evaluate the importance of the non-negligible beam–target reaction for inertial confinement fusion schemes with large implosion velocity such as double-cone ignition and impact ignition, in which the high-speed plasmas collide with each other to realize plasma ignition.
. The improved method will make large corrections to evaluate the importance of the non-negligible beam–target reaction for inertial confinement fusion schemes with large implosion velocity such as double-cone ignition and impact ignition, in which the high-speed plasmas collide with each other to realize plasma ignition.