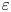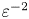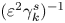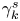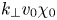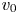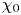1. Introduction
Exact solutions of the governing equations of a dynamical system in general yield some representation of the associated spatiotemporal structure. In fluid mechanical models, such as incompressible magnetohydrodynamics (MHD) (Biskamp Reference Biskamp2008), for which the governing equation does not readily admit explicit closed-form solutions beyond the simplest cases, an alternative is to determine the space–time structure via observation and measurement of some physical quantity whose evolution is determined by the set of laws describing the said model. The obvious shortcoming of this technique is the sheer impossibility of simultaneously measuring all of the relevant space for all instances of time during the entire desired duration of observation; there are always limitations placed on the maximally achievable spatial and temporal resolutions. In the case of single-point measurement, a time series is recorded describing the local variations in some property of the flow. When the mean bulk velocity field is much larger than its associated turbulent fluctuations, one may evoke the Taylor hypothesis (TH) (Taylor Reference Taylor1938) and treat the time series as the spatial shape of a passing (albeit unchanging otherwise) frozen structure. This is analogous to the analysis of linear wave propagation when its characteristic time scale is much shorter than that of any other processes present and the wave's dispersion relation (DR) may be employed to evaluate the time series. These techniques allow for a one-point two-time correlation to be expressed as a two-point one-time correlation, conveniently providing an injective mapping between the flow's temporal and spatial structure; however, it is of crucial importance to emphasize that these are in general independent constructs (Matthaeus et al. Reference Matthaeus2019). In regimes where the TH/DR are not applicable, other means are required to distinguish between potentially comparable-strength competing flow effects and elucidate the overall space–time structure. To this end, a body of interest is the hierarchy of functions describing the statistical relationships between points in a flow as a function of their space–time separation $(\boldsymbol {x}'-\boldsymbol {x},t'-t)=(\boldsymbol {r},\tau )$![]() . Two functions of fundamental importance, related by a spatial Fourier transform, are the two-point two-time correlation function of statistically stationary and homogeneous turbulence
. Two functions of fundamental importance, related by a spatial Fourier transform, are the two-point two-time correlation function of statistically stationary and homogeneous turbulence
and two-time energy spectrum
The correlation (1.1) suggests the similarity in value of some quantity $f$![]() at points in a flow separated across space–time by $(\boldsymbol {r},\tau )$
at points in a flow separated across space–time by $(\boldsymbol {r},\tau )$![]() , while the spectrum (1.2) is the autocorrelation of Fourier mode $\boldsymbol {k}$
, while the spectrum (1.2) is the autocorrelation of Fourier mode $\boldsymbol {k}$![]() for the transform of the said quantity.
for the transform of the said quantity.
They are of particular interest for the Parker Solar Probe mission (Fox et al. Reference Fox, Velli, Bale, Decker, Driesman, Howard, Kasper, Kinnison, Kusterer, Lario, Lockwood, McComas, Raouafi and Szabo2016), as it remains an open question whether the TH will hold in the vicinity of perihelion (Chhiber et al. Reference Chhiber, Usmanov, Matthaeus, Parashar and Goldstein2019; Perez et al. Reference Perez, Bourouaine, Chen and Raouafi2021). The behaviours of these two functions have been investigated extensively in the context of MHD (Matthaeus et al. Reference Matthaeus, Dasso, Weygand, Kivelson and Osman2010; Servidio et al. Reference Servidio, Carbone, Dmitruk and Matthaeus2011; Weygand et al. Reference Weygand, Matthaeus, Kivelson and Dasso2013; Lugones et al. Reference Lugones, Dmitruk, Mininni, Wan and Matthaeus2016; Narita Reference Narita2017; Bourouaine & Perez Reference Bourouaine and Perez2018, Reference Bourouaine and Perez2019; Perez, Azelis & Bourouaine Reference Perez, Azelis and Bourouaine2020; Perez & Bourouaine Reference Perez and Bourouaine2020). In particular, Perez et al. (Reference Perez, Azelis and Bourouaine2020) derived an integro-differential equation (IDE) for an Eulerian scale-dependent time correlation (SDTC) associated with the model of reduced MHD (RMHD) using a cumulant-discard-based formulation (see for instance Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000, Reference Galtier, Nazarenko, Newell and Pouquet2002; Galtier & Chandran Reference Galtier and Chandran2006) of weak turbulence. They then investigated approximations to a generic form of this IDE in the asymptotic limits of long and short-time lags. Solutions were found in terms of integrals of the two-time energy spectrum, without explicit calculation of these integrals or the spectrum itself. Their SDTC exhibited Gaussian behaviour for short-time lag (which coincides with the limit of strong MHD turbulence) and exponential for long-time lag.
In this work, we derive an ordinary differential equation (ODE) for a two-time energy spectrum (which fortuitously yields an SDTC) using an a posteriori (AP) formulation of weak turbulence (Benney & Newell Reference Benney and Newell1967, Reference Benney and Newell1969) (those unfamiliar may find a demonstration of this technique to obtain a wave kinetic equation (WKE) in Appendix B) applied to the model of RMHD. The ODE is then exactly solved, providing an explicit spectrum that is completely specified in terms of appropriate initial conditions. The remainder of the paper is structured as follows. In § 2, an equation for the nonlinear evolution of shear-Alfvén mode Fourier amplitudes is developed from first principles. In § 3, the AP technique is used to obtain a two-time energy spectrum accurate to the lowest non-trivial order in perturbation. Section 4 reviews conclusions drawn from the functional form of this spectrum.
2. Model
The governing equations of an electrically conducting incompressible fluid are
where $\boldsymbol {v}$![]() is the velocity field, $\boldsymbol {B}$
is the velocity field, $\boldsymbol {B}$![]() is the magnetic field, $\eta$
is the magnetic field, $\eta$![]() is the magnetic diffusivity, $\nu$
is the magnetic diffusivity, $\nu$![]() is the kinematic viscosity, $\mu _0$
is the kinematic viscosity, $\mu _0$![]() is the magnetic permeability and $P$
is the magnetic permeability and $P$![]() is the total pressure from thermal $p$
is the total pressure from thermal $p$![]() and magnetic contributions
and magnetic contributions
Equation (2.1) describes momentum conservation and it simply states Newton's second law for a conducting fluid. Equation (2.2) is referred to as either the induction equation or Faraday's law, and describes the temporal evolution of the magnetic field due to convective and dissipative effects. Equations (2.3) and (2.4) are the constraints that the velocity and magnetic fields be divergenceless. The former is the incompressibility assumption made in this work while the latter is one of the four fundamental laws of electromagnetism, the non-existence of isolated magnetic charges. This magnetic fluid model provides a reasonable description of magnetized plasmas on scales much larger than microscopic plasma scales where the energy of these fields is typically dissipated. In magnetized plasmas, the magnetic field is written as the sum of a uniform field $\boldsymbol {B}_0$![]() in the direction $\hat {\boldsymbol {b}}$
in the direction $\hat {\boldsymbol {b}}$![]() and non-uniform $\boldsymbol {B}_1$
and non-uniform $\boldsymbol {B}_1$![]() such that $\boldsymbol {B}=\boldsymbol {B}_0+\boldsymbol {B}_1$
such that $\boldsymbol {B}=\boldsymbol {B}_0+\boldsymbol {B}_1$![]() . In this instance a change of variables originally proposed by Elsasser (Reference Elsasser1950) may be employed
. In this instance a change of variables originally proposed by Elsasser (Reference Elsasser1950) may be employed
Adding and subtracting (2.1) and (2.2) while utilizing (2.6) results in
where $\boldsymbol {v}_{{A}}= {\boldsymbol {B}_0}/{\sqrt {\mu _0 \rho }}$![]() , $\boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol {z}^{\pm } = 0$
, $\boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol {z}^{\pm } = 0$![]() because of incompressibility, and for simplicity, we have taken $\nu =\eta$
because of incompressibility, and for simplicity, we have taken $\nu =\eta$![]() . Equation (2.7) are known as the incompressible MHD equations in the Elsasser form. These equations describe the evolution of Alfvén waves with amplitude $\boldsymbol {z}^{\pm }$
. Equation (2.7) are known as the incompressible MHD equations in the Elsasser form. These equations describe the evolution of Alfvén waves with amplitude $\boldsymbol {z}^{\pm }$![]() propagating along $\boldsymbol {B}_0$
propagating along $\boldsymbol {B}_0$![]() at speed $\boldsymbol v_{{A}}$
at speed $\boldsymbol v_{{A}}$![]() in opposite directions. For a recent review of Alfvén waves, see Chen & Zonca (Reference Chen and Zonca2016). An additional assumption that we make in this work is that Elsasser fields, representing Alfvénic perturbations of the guide field $\boldsymbol B_0$
in opposite directions. For a recent review of Alfvén waves, see Chen & Zonca (Reference Chen and Zonca2016). An additional assumption that we make in this work is that Elsasser fields, representing Alfvénic perturbations of the guide field $\boldsymbol B_0$![]() , have polarization in the plane perpendicular to $\boldsymbol B_0$
, have polarization in the plane perpendicular to $\boldsymbol B_0$![]() . This assumption renders (2.7) equivalent to the RMHD model (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1974; Strauss Reference Strauss1976), which ignores the dynamics of the pseudo-Alfvén wave modes and describes the nonlinear evolution of shear-Alfvén waves. In fact, it can be shown that in the weak turbulence regime, the dynamics of pseudo-Alfvén waves decouples from the shear-Alfvén waves, in which case a wave turbulence closure can be achieved from the much simpler RMHD equations (Galtier & Chandran Reference Galtier and Chandran2006; Perez & Boldyrev Reference Perez and Boldyrev2008). After considerable manipulation (see Appendix A for details), it can be shown from (2.7) that the nonlinear evolution of shear-Alfvén wave Fourier-amplitudes $\phi ^\pm _k \equiv \phi ^\pm (\boldsymbol {k},t)$
. This assumption renders (2.7) equivalent to the RMHD model (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1974; Strauss Reference Strauss1976), which ignores the dynamics of the pseudo-Alfvén wave modes and describes the nonlinear evolution of shear-Alfvén waves. In fact, it can be shown that in the weak turbulence regime, the dynamics of pseudo-Alfvén waves decouples from the shear-Alfvén waves, in which case a wave turbulence closure can be achieved from the much simpler RMHD equations (Galtier & Chandran Reference Galtier and Chandran2006; Perez & Boldyrev Reference Perez and Boldyrev2008). After considerable manipulation (see Appendix A for details), it can be shown from (2.7) that the nonlinear evolution of shear-Alfvén wave Fourier-amplitudes $\phi ^\pm _k \equiv \phi ^\pm (\boldsymbol {k},t)$![]() is governed by the following equations:
is governed by the following equations:
where $s = +$![]() or $-$
or $-$![]() is a compact notation for the Elsasser fields, $\varepsilon$
is a compact notation for the Elsasser fields, $\varepsilon$![]() is a small ordering parameter used to represent the relative strength of the wave amplitudes, $\omega _k^s\equiv sk_\|v_{A}$
is a small ordering parameter used to represent the relative strength of the wave amplitudes, $\omega _k^s\equiv sk_\|v_{A}$![]() is the Alfvén-waves DR, $\delta _{k,pq}\equiv \delta ^{(3)}(\boldsymbol {k}-\boldsymbol {p}-\boldsymbol {q})$
is the Alfvén-waves DR, $\delta _{k,pq}\equiv \delta ^{(3)}(\boldsymbol {k}-\boldsymbol {p}-\boldsymbol {q})$![]() , and
, and
The Fourier-transformed Elsasser fields $\boldsymbol z_k^s\equiv \boldsymbol z^s(\boldsymbol k,t)$![]() are then obtained from $\phi ^s_{k}(t)$
are then obtained from $\phi ^s_{k}(t)$![]() as
as
where $\hat {\boldsymbol {e}}_k \equiv \boldsymbol {k}_\perp \times \hat {\boldsymbol {b}}/k_\perp$![]() is the unit vector in the direction perpendicular to both the guide magnetic field and the wavevector $\boldsymbol k$
is the unit vector in the direction perpendicular to both the guide magnetic field and the wavevector $\boldsymbol k$![]() .
.
For sufficiently small wave amplitudes ($\varepsilon \ll 1$![]() ), (2.8) describes weakly nonlinear interacting shear Alfvén waves. It broadly states that waves with amplitude $\varepsilon |\phi ^s_{k}(t)|$
), (2.8) describes weakly nonlinear interacting shear Alfvén waves. It broadly states that waves with amplitude $\varepsilon |\phi ^s_{k}(t)|$![]() and wavevector $\boldsymbol {k}$
and wavevector $\boldsymbol {k}$![]() travelling in the direction $s\hat {\boldsymbol {b}}$
travelling in the direction $s\hat {\boldsymbol {b}}$![]() will evolve in time according to all possible sets of counter-propagating waves $\boldsymbol {p}$
will evolve in time according to all possible sets of counter-propagating waves $\boldsymbol {p}$![]() and $\boldsymbol {q}$
and $\boldsymbol {q}$![]() with wavevectors whose sum is $\boldsymbol {k}$
with wavevectors whose sum is $\boldsymbol {k}$![]() , imposed by the delta function constraint $\delta _{k,pq}$
, imposed by the delta function constraint $\delta _{k,pq}$![]() . Equation (2.8) in combination with an interaction representation will serve as the fundamental building block for subsequent construction of the statistical one- and two-time cumulant hierarchies in this work. Contained within the latter group of functions, we define the two-time power spectrum $h(\boldsymbol k;t,t')$
. Equation (2.8) in combination with an interaction representation will serve as the fundamental building block for subsequent construction of the statistical one- and two-time cumulant hierarchies in this work. Contained within the latter group of functions, we define the two-time power spectrum $h(\boldsymbol k;t,t')$![]() as
as
In addition to being a fundamental quantity in turbulence theory, explicit knowledge of (2.11) could also potentially suggest the space–time distribution of turbulent energy in a plasma for which this model holds. One property of $h^s(\boldsymbol k,t,t')$![]() is that when temporal separation is nullified and $t'=t$
is that when temporal separation is nullified and $t'=t$![]() , the two-time energy spectrum reduces to its one-time equivalent
, the two-time energy spectrum reduces to its one-time equivalent
This also permits $h^s(\boldsymbol k,t,t')$![]() to be defined in terms of the Eulerian SDTC function
to be defined in terms of the Eulerian SDTC function
such that $\varGamma ^s(\boldsymbol {k},t,t) = 1$![]() . We recast (2.13) under the assumption of stationary turbulence in terms of the time lag $\tau = t'-t$
. We recast (2.13) under the assumption of stationary turbulence in terms of the time lag $\tau = t'-t$![]()
By virtue of the nonlinear energy exchange between counter-propagating fluctuations, the SDTC possesses the property $\lim _{\tau \rightarrow \infty }\varGamma ^s(\boldsymbol {k},\tau ) = 0.$![]() Noting definitions (2.11) and (2.12), (2.14) formulates $\varGamma ^s(\boldsymbol {k},\tau )$
Noting definitions (2.11) and (2.12), (2.14) formulates $\varGamma ^s(\boldsymbol {k},\tau )$![]() as
as
Equation (2.15) suggests that $\varGamma ^s(\boldsymbol {k},\tau )$![]() describes the normalized autocorrelation of time lag $\tau$
describes the normalized autocorrelation of time lag $\tau$![]() for Alfvénic fluctuations with wavevector $\boldsymbol {k}$
for Alfvénic fluctuations with wavevector $\boldsymbol {k}$![]() . It is indicative of the extent to which the dynamics, given time $\tau$
. It is indicative of the extent to which the dynamics, given time $\tau$![]() to act, have redistributed the Alfvénic energy content of the system over a given length scale due to both linear propagation and nonlinear interactions. Lastly, it is also worth noting that the two-point two-time correlation function for Elsasser fields is obtained from the two-time power spectra via the following Fourier transform:
to act, have redistributed the Alfvénic energy content of the system over a given length scale due to both linear propagation and nonlinear interactions. Lastly, it is also worth noting that the two-point two-time correlation function for Elsasser fields is obtained from the two-time power spectra via the following Fourier transform:
3. Closure
In this section, we use a wave-turbulence closure to derive an ODE for a two-time energy spectrum for the model of weakly turbulent incompressible MHD. The ODE is then integrated, yielding the main result of this paper, a spectrum suggesting exponential decay in Fourier mode autocorrelation due to nonlinear interactions between counter-propagating shear-Alfvén waves.
3.1. Preliminary closure discourse
The method of wave-turbulence closure refers to a set of various techniques by which the statistical closure of a hierarchy of moments of a random field is treated as a perturbation problem for a system of weakly interacting modes. The notion of a weak interaction refers to the existence of some small parameter $\varepsilon$![]() in terms of which either wave amplitudes or fluid moments may be perturbatively expanded to approximately solve the nonlinear differential equations characterizing these types of systems. Furthermore, $\varepsilon$
in terms of which either wave amplitudes or fluid moments may be perturbatively expanded to approximately solve the nonlinear differential equations characterizing these types of systems. Furthermore, $\varepsilon$![]() is representative of the ratio of time scales for linear to nonlinear processes ($\varepsilon \sim t_{\rm lin}/t_{\rm nl}$
is representative of the ratio of time scales for linear to nonlinear processes ($\varepsilon \sim t_{\rm lin}/t_{\rm nl}$![]() ) and indicative of the strength of nonlinear interaction. In RMHD phenomenology, $\varepsilon$
) and indicative of the strength of nonlinear interaction. In RMHD phenomenology, $\varepsilon$![]() weights the time for counter-propagating Alfvén waves to pass through each other versus the characteristic time required for nonlinear interaction during their spatial coincidence. This notion is quantified for a fluctuation with wavevector $\boldsymbol {k}=(k_\parallel,k_\perp )$
weights the time for counter-propagating Alfvén waves to pass through each other versus the characteristic time required for nonlinear interaction during their spatial coincidence. This notion is quantified for a fluctuation with wavevector $\boldsymbol {k}=(k_\parallel,k_\perp )$![]() in the form
in the form
This definition of $\varepsilon$![]() accounts for particular notable aspects of MHD turbulence phenomenology. For instance, the concept of critical balance (Sridhar & Goldreich Reference Sridhar and Goldreich1994; Goldreich & Sridhar Reference Goldreich and Sridhar1995, Reference Goldreich and Sridhar1997) for which a transition from weak to strong turbulence occurs is clearly demonstrated by the limit $\varepsilon \rightarrow 1$
accounts for particular notable aspects of MHD turbulence phenomenology. For instance, the concept of critical balance (Sridhar & Goldreich Reference Sridhar and Goldreich1994; Goldreich & Sridhar Reference Goldreich and Sridhar1995, Reference Goldreich and Sridhar1997) for which a transition from weak to strong turbulence occurs is clearly demonstrated by the limit $\varepsilon \rightarrow 1$![]() . In addition, the presence of strong turbulence in the neighbourhood of $k_\parallel =0$
. In addition, the presence of strong turbulence in the neighbourhood of $k_\parallel =0$![]() (Galtier & Chandran Reference Galtier and Chandran2006) coincides with $\varepsilon$
(Galtier & Chandran Reference Galtier and Chandran2006) coincides with $\varepsilon$![]() becoming appreciably large; counter-propagating waves of sufficient parallel extent will interact for ample temporal intervals such that the nonlinearity would not be considered weak. Generally speaking, there exists a range of fluctuation length scales for which $\varepsilon \geq O(1)$
becoming appreciably large; counter-propagating waves of sufficient parallel extent will interact for ample temporal intervals such that the nonlinearity would not be considered weak. Generally speaking, there exists a range of fluctuation length scales for which $\varepsilon \geq O(1)$![]() and the weak turbulence closure is not valid. The aforementioned fundamentally different linear and nonlinear dynamical processes occurring over disparate time scales are associated with the presence of a singular (as opposed to a regular) perturbation.
and the weak turbulence closure is not valid. The aforementioned fundamentally different linear and nonlinear dynamical processes occurring over disparate time scales are associated with the presence of a singular (as opposed to a regular) perturbation.
In a regular perturbation problem, the solution of the perturbed system (for $0 < \varepsilon \ll 1$![]() ) is qualitatively the same as the case for null-perturbation in which $\varepsilon = 0$
) is qualitatively the same as the case for null-perturbation in which $\varepsilon = 0$![]() . These solutions are characterized by a convergent expansion in $\varepsilon$
. These solutions are characterized by a convergent expansion in $\varepsilon$![]() , describing a combination of the $\varepsilon =0$
, describing a combination of the $\varepsilon =0$![]() system and higher-order corrections in response to the regular perturbation. In contrast, a singular perturbation problem features marked differences between the perturbed and unperturbed systems. Additionally, solutions take the form of asymptotic and potentially divergent expansions in terms of $\varepsilon$
system and higher-order corrections in response to the regular perturbation. In contrast, a singular perturbation problem features marked differences between the perturbed and unperturbed systems. Additionally, solutions take the form of asymptotic and potentially divergent expansions in terms of $\varepsilon$![]() (Hunter Reference Hunter2004). For the RMHD model used in this work, the case of $\varepsilon = 0$
(Hunter Reference Hunter2004). For the RMHD model used in this work, the case of $\varepsilon = 0$![]() (as applied to (2.8)) corresponds to a trivially solvable ODE in the Fourier domain describing pure Alfvénic propagation and an absence of nonlinear interaction between counter-propagating waves; the time required for nonlinear interactions to occur is infinite, and the linear wave period is the only genuine dynamical time scale of interest in this situation. Non-zero, albeit small values of $\varepsilon$
(as applied to (2.8)) corresponds to a trivially solvable ODE in the Fourier domain describing pure Alfvénic propagation and an absence of nonlinear interaction between counter-propagating waves; the time required for nonlinear interactions to occur is infinite, and the linear wave period is the only genuine dynamical time scale of interest in this situation. Non-zero, albeit small values of $\varepsilon$![]() describe a qualitatively different set of systems for which these waves may interact with one another over a time scale much longer than the linear wave period. These interactions then produce divergences in naïve perturbative expansions of dynamical expressions constructed from (2.8). Said divergences manifest as explicit polynomial time dependence found in solutions of the perturbed governing equations, resulting in higher-order terms eventually becoming larger than leading order $O(\varepsilon ^0)$
describe a qualitatively different set of systems for which these waves may interact with one another over a time scale much longer than the linear wave period. These interactions then produce divergences in naïve perturbative expansions of dynamical expressions constructed from (2.8). Said divergences manifest as explicit polynomial time dependence found in solutions of the perturbed governing equations, resulting in higher-order terms eventually becoming larger than leading order $O(\varepsilon ^0)$![]() after the passage of sufficient amounts of time.
after the passage of sufficient amounts of time.
Methods for handling singular perturbations (see for instance Bender & Orszag Reference Bender and Orszag2009) can be classified according to whether the underlying differential equation is concerned with variations in space (e.g. the WKB approximation) or time (e.g. Poincaré–Lindstedt or the method of multiple scales). In this work, divergences associated with the temporally singular nature of (2.8) arising in asymptotic expansion of the two-time energy spectrum are dealt with using an AP method developed in Benney & Newell (Reference Benney and Newell1967) and Benney & Newell (Reference Benney and Newell1969). The AP method solves differential equations by naïvely assuming a regular perturbative solution to the desired order in $\varepsilon$![]() followed by renormalization of the zero-order term to remove any divergences arising due to the singular nature of the problem. The combination of asymptotic time-domain analysis and renormalization yields statistical closure as well as a dynamical description of the system, accurate through time scales of the order of the initial expansion.
followed by renormalization of the zero-order term to remove any divergences arising due to the singular nature of the problem. The combination of asymptotic time-domain analysis and renormalization yields statistical closure as well as a dynamical description of the system, accurate through time scales of the order of the initial expansion.
The equivalence of this technique with the perhaps more commonly known method of multiple scales (among other methods for temporally singular perturbation problems) is trivial to demonstrate and may be found in a solution of the van der Pol equation in the introduction of Benney & Newell (Reference Benney and Newell1967). Application of the AP method to systems of weakly interacting dispersive waves may be found in the main body of the aforementioned work, while the equivalence of wave amplitude and cumulant-based expansions (we prefer the latter in this paper as the quantities of interest are functions in a statistical hierarchy) is demonstrated in the second and third sections of Benney & Newell (Reference Benney and Newell1969). In addition, it may be prudent (and is strongly recommended) for the uninitiated reader to peruse the demonstration of the AP method presented in Appendix B, which derives the WKE for the energy spectrum of incompressible MHD originally found by Galtier et al. (Reference Galtier, Nazarenko, Newell and Pouquet2000).
We admit that the level of rigor used in our analysis may seemingly verge on tedious mathematical verbosity, but argue that it is ultimately necessary for posterity to both understand the process by which one obtains these results, and how they may reapply these methods to their own nonlinear wave equations. The amount of detail presented at various points in for instance Benney & Newell (Reference Benney and Newell1967), Benney & Newell (Reference Benney and Newell1969), Galtier et al. (Reference Galtier, Nazarenko, Newell and Pouquet2000), Galtier et al. (Reference Galtier, Nazarenko, Newell and Pouquet2002), Galtier & Chandran (Reference Galtier and Chandran2006) and Newell & Rumpf (Reference Newell and Rumpf2011) may leave the mathematically curious, albeit wave-turbulence naïve, longing for a clearer and convincing explanation of the closure details. The reader who is more familiar (or not concerned) with this process may, in contrast, briefly glance over the details presented herein and proceed to the final spectral results found at the end of § 3.3.
If one were to momentarily forget any notion of plasma physics, the closures presented in this section as well as that of Appendix B amount to the solution of general singular perturbation problems characteristic of a first-order ODE whose linear homogeneous solution corresponds to a sinusoidal oscillation, which is then subject to an inhomogeneity in the form of a weak quadratic nonlinearity; the differences between the two derivations only arise in the physical interpretation of the desired functions and the amount of required analytical computation. The WKE supplies a description of a given Elsasser field Fourier mode's energetic tendencies according to integration over all nonlinear interactions in which it partakes at some instance in time. The two-time energy spectrum models the amount by which a given mode has become statistically dissimilar from itself (after some time $\tau$![]() ) due to being both transported through space by linear advection and distorted due to the aforementioned nonlinear interactions. While the naming convention for this function may somehow suggest that two different times are explicitly being evoked upon its evaluation, the assumption of stationary turbulence, that time-domain statistics are purely a function of the lag $\tau =t'-t$
) due to being both transported through space by linear advection and distorted due to the aforementioned nonlinear interactions. While the naming convention for this function may somehow suggest that two different times are explicitly being evoked upon its evaluation, the assumption of stationary turbulence, that time-domain statistics are purely a function of the lag $\tau =t'-t$![]() (and not the ‘base-time’ $t$
(and not the ‘base-time’ $t$![]() ) between two instances of the Elsasser fields, results in the information associated with temporal decorrelation being encoded onto a single variable. In addition, it is easily observed that the application of the limit of $\tau =0$
) between two instances of the Elsasser fields, results in the information associated with temporal decorrelation being encoded onto a single variable. In addition, it is easily observed that the application of the limit of $\tau =0$![]() to the two-time energy closure is approximately equivalent to performing half of the Appendix B derivation.
to the two-time energy closure is approximately equivalent to performing half of the Appendix B derivation.
In this section, the multiple scales ($\tau _0 = \varepsilon ^0\tau$![]() and $\tau _2 = \varepsilon ^2 \tau$
and $\tau _2 = \varepsilon ^2 \tau$![]() ) arising in our implementation of the AP method are merely time lags of different order in $\varepsilon$
) arising in our implementation of the AP method are merely time lags of different order in $\varepsilon$![]() . We exploit the creation of these artificial degrees of freedom (a process that is obviously not unique to the AP method, and rather ubiquitous in temporally singular perturbative techniques) to clearly isolate linear from nonlinear influence upon Fourier mode autocorrelation. At leading order, the autocorrelation oscillates with time lag $\tau =O(\varepsilon ^0)$
. We exploit the creation of these artificial degrees of freedom (a process that is obviously not unique to the AP method, and rather ubiquitous in temporally singular perturbative techniques) to clearly isolate linear from nonlinear influence upon Fourier mode autocorrelation. At leading order, the autocorrelation oscillates with time lag $\tau =O(\varepsilon ^0)$![]() due to Alfvénic propagation, while it will be shown to exponentially decay with time lag $\tau = O(\varepsilon ^{-2})$
due to Alfvénic propagation, while it will be shown to exponentially decay with time lag $\tau = O(\varepsilon ^{-2})$![]() due to participation in resonant nonlinear energy transfer. The intuition is that a relatively large number of wave oscillations will have occurred before a time of $O(\varepsilon ^{-2})$
due to participation in resonant nonlinear energy transfer. The intuition is that a relatively large number of wave oscillations will have occurred before a time of $O(\varepsilon ^{-2})$![]() elapses and a single nonlinear interaction may transpire. The notion of the existence of these temporally disparate processes is not novel or original and is in fact identical to the foundation upon which the WKE (B64) is predicated. Nonetheless, the underlying mathematics is not concerned with the assignment of the appropriate physical meaning to the multiple scales. Reduced to their essence, the statistical closures presented in this work are but applications of rather elementary and commonplace singular perturbative methods for solving nonlinear differential equations. One could write down a generic form of the procedure lacking in any even remotely imaginable conceptualization attributed to the function or superficially distinct instances of the lone independent variable and the process would remain the same. However, such a presentation is outside of the intended scope of this work and is omitted; in this context, it would only serve as a redundant and repetitive abstraction of the analysis found in the subsequent subsections. The remainder of this section is dedicated to the development and closure of a two-time cumulant hierarchy, resulting in a functional description of a two-time energy spectrum accurate through time lag $\tau =O(\varepsilon ^{-2})$
elapses and a single nonlinear interaction may transpire. The notion of the existence of these temporally disparate processes is not novel or original and is in fact identical to the foundation upon which the WKE (B64) is predicated. Nonetheless, the underlying mathematics is not concerned with the assignment of the appropriate physical meaning to the multiple scales. Reduced to their essence, the statistical closures presented in this work are but applications of rather elementary and commonplace singular perturbative methods for solving nonlinear differential equations. One could write down a generic form of the procedure lacking in any even remotely imaginable conceptualization attributed to the function or superficially distinct instances of the lone independent variable and the process would remain the same. However, such a presentation is outside of the intended scope of this work and is omitted; in this context, it would only serve as a redundant and repetitive abstraction of the analysis found in the subsequent subsections. The remainder of this section is dedicated to the development and closure of a two-time cumulant hierarchy, resulting in a functional description of a two-time energy spectrum accurate through time lag $\tau =O(\varepsilon ^{-2})$![]() .
.
3.2. Development of two-time cumulant hierarchy
In this subsection, we develop a set of differential equations describing the evolution of a two-time cumulant hierarchy as a function of time lag. The set is developed with the intention of finding the leading-order behaviour of the two-time power spectrum $h_k^s(t,t')$![]() defined by (2.11). To facilitate analysis, an interaction representation
defined by (2.11). To facilitate analysis, an interaction representation
is introduced to separate linear and nonlinear effects on $h_k^s(t,t')$![]()
The slowly varying (i.e. the portion changing due to nonlinear interactions) two-time power spectrum is then defined as
In addition, shear-Alfvén Fourier amplitudes will then evolve nonlinearly according to a version of (2.8) recast as
We proceed to generate a hierarchy developed from (3.4) using (3.5) via wave turbulence in a manner comparable to the WKE derivation of Appendix B. A similar secularity associated with resonant interactions between counter-propagating Alfvén waves occurs for time lags of order $O(\varepsilon ^{-2})$![]() and subsequent reordering of the asymptotic expansion for $\tilde h_k^s(t,t')$
and subsequent reordering of the asymptotic expansion for $\tilde h_k^s(t,t')$![]() yields leading-order behaviour.
yields leading-order behaviour.
The process begins with the generation of a set of differential equations describing time-lagged evolution of the second- and third-order (in statistics) two-time cumulants. We begin with an approach comparable to § B.1 of this work by differentiating $\tilde h_k^s(t,t')$![]() of (3.4), but with respect to $t'$
of (3.4), but with respect to $t'$![]() instead of $t$
instead of $t$![]() :
:
A two-time third-order cumulant is encountered of the form
and we have found a closure problem for a hierarchy of two-time statistical functions. Thus, we seek an equation governing the lagged evolution of the third-order cumulant
A fourth-order moment decomposes into a fourth-order cumulant and all possible products of second-order cumulants. Noting the fast decorrelation of counter-propagating Alfvén waves (which may be demonstrated via the Riemann–Lebesgue lemma equation (B34)), the fourth-order moments on the right-hand side of (3.9) may be evaluated as
and
The fourth-order moments on the right-hand side of (3.9) containing two-time statistics simplify analogously with (B4) and (B14) and the third-order cumulant denoted by (3.7) evolves as

The third term on the right-hand side of (3.13) may be integrated over wave vectors from noting the delta function correlations
where we have used the fact that
Equation (3.13) can then be expressed as

Through the lens of wave-turbulence theory, (3.6) and (3.16) are sufficient to close the two-time statistical hierarchy through $O(\varepsilon ^2)$![]() in perturbation, and obtain an explicit expression for the two-time energy spectrum.
in perturbation, and obtain an explicit expression for the two-time energy spectrum.
3.3. Weak turbulence closure for two-time energy spectrum
We naïvely perturb the hierarchy of time-lagged differential equations derived in the previous subsection and search for secular terms (associated with divergent expansions) by investigating the asymptotic behaviour of (3.6) and (3.16) for lag through order $\tau = O(\varepsilon ^{-2})$![]() . Those who are unfamiliar with the process by which we seek out secularities may refer to the elementary functional analysis presented in Appendix B.1. Renormalization of the leading-order two-time energy spectrum using the AP method yields a solution of the said function describing exponential decay due to nonlinear interactions.
. Those who are unfamiliar with the process by which we seek out secularities may refer to the elementary functional analysis presented in Appendix B.1. Renormalization of the leading-order two-time energy spectrum using the AP method yields a solution of the said function describing exponential decay due to nonlinear interactions.
Equations (3.6) and (3.16) are subject to the asymptotic expansions
After substitution and change of variables $t' = t+\tau$![]() under the assumption of statistically stationary turbulence, the resulting perturbed hierarchy of equations is of the form
under the assumption of statistically stationary turbulence, the resulting perturbed hierarchy of equations is of the form

Before proceeding through solving the hierarchy, we observe the behaviour of the two-time cumulants in configuration space, where they correspond to space–time correlation functions. The two-time energy spectrum is related to the two-point two-time correlation function as
A feature appears at this statistical order, which is absent from the energy spectrum transform expression (B37) in the form of an oscillation with respect to time lag. Terms in expansion (3.17) which do not identically cancel the complex phase ${\rm e}^{{\rm i}\omega _k^s\tau }$![]() present in (3.25) will decay in configuration space at large values of $\tau$
present in (3.25) will decay in configuration space at large values of $\tau$![]() as $O(\tau ^{-1})$
as $O(\tau ^{-1})$![]() in accordance with the Riemann–Lebesgue lemma and (B35). However, the secular terms in the expansion (3.17) will lead to exponential decay in the two-time energy spectrum due to resonant interactions, providing a faster and more stringent temporal decorrelation rate. The two-time third-order cumulant corresponds to a three-point two-time correlation function as
in accordance with the Riemann–Lebesgue lemma and (B35). However, the secular terms in the expansion (3.17) will lead to exponential decay in the two-time energy spectrum due to resonant interactions, providing a faster and more stringent temporal decorrelation rate. The two-time third-order cumulant corresponds to a three-point two-time correlation function as

Oscillations are encountered involving both time and time lag. It will be shown that there is still a resonance present (analogous to that of one-time closure theory) for which the complex phase ${\rm e}^{-2\mathrm i\omega _q^st}$![]() is exactly cancelled at any given moment in time $t$
is exactly cancelled at any given moment in time $t$![]() , leading to a secularity. A similar form of configuration space correlation function may be shown for the two-time fourth-order cumulant.
, leading to a secularity. A similar form of configuration space correlation function may be shown for the two-time fourth-order cumulant.
Proceeding through the expansion, we observe $h^s_{0,k}(\tau )$![]() and $Q^{(s,s,-s)(3)}_{0,-kp}(\tau )$
and $Q^{(s,s,-s)(3)}_{0,-kp}(\tau )$![]() are independent of the time lag to leading order. Direct integration of (3.22) results in
are independent of the time lag to leading order. Direct integration of (3.22) results in

By a similar token, integration of (3.23) with respect to $\tau$![]() yields
yields

Substitution of the second term of (3.28) into the Fourier transform equation (3.26)

yields cancellation of the complex phase ${\rm e}^{-2\mathrm i\omega _q^st}$![]() , implying that this particular three-wave interaction is still resonant at each particular instance in time $t$
, implying that this particular three-wave interaction is still resonant at each particular instance in time $t$![]() in a manner similar to (B52). This term will lead to a secularity in the two-time energy spectrum at $O(\varepsilon ^2)$
in a manner similar to (B52). This term will lead to a secularity in the two-time energy spectrum at $O(\varepsilon ^2)$![]() in expansion (3.17). It should be noted that this correlation still decays as $O(\tau ^{-1})$
in expansion (3.17). It should be noted that this correlation still decays as $O(\tau ^{-1})$![]() due to the Riemann–Lebesgue lemma as the modes that interacted at $\tau =0$
due to the Riemann–Lebesgue lemma as the modes that interacted at $\tau =0$![]() propagate away from each other as characterized by the remaining complex exponentials. Substitution of (3.28) into (3.24) results in
propagate away from each other as characterized by the remaining complex exponentials. Substitution of (3.28) into (3.24) results in

Noting the relationships
and
(3.30) is recast as

Direct integration of (3.33) then results in

The procedure for evaluating the long $\tau$![]() behaviour is nearly identical to the one-time closure. Here $\tilde {h}^s_{1,k}(\tau )$
behaviour is nearly identical to the one-time closure. Here $\tilde {h}^s_{1,k}(\tau )$![]() and $Q^{(s,s,-s)(3)}_{1,-kp}(\tau )$
and $Q^{(s,s,-s)(3)}_{1,-kp}(\tau )$![]() only depend on functions of the form $\varDelta _\tau (x)$
only depend on functions of the form $\varDelta _\tau (x)$![]() and are thus well-behaved in the limit $\tau \rightarrow \infty$
and are thus well-behaved in the limit $\tau \rightarrow \infty$![]() . The first term in (3.34) is of the same form (B59) and is thus non-secular. Meanwhile, the second term is of the form (B58), and in a manner analogous to the one-time case, is unbounded in time. In anticipation of subsequent calculations, we consider the possibility of time lag on the interval $-\infty < \tau < \infty$
. The first term in (3.34) is of the same form (B59) and is thus non-secular. Meanwhile, the second term is of the form (B58), and in a manner analogous to the one-time case, is unbounded in time. In anticipation of subsequent calculations, we consider the possibility of time lag on the interval $-\infty < \tau < \infty$![]() . It was demonstrated in the appendix of Benney & Newell (Reference Benney and Newell1969) that the case of $\tau < 0$
. It was demonstrated in the appendix of Benney & Newell (Reference Benney and Newell1969) that the case of $\tau < 0$![]() amounts to multiplying delta functions present in the asymptotic expressions such as (B58) by $-1$
amounts to multiplying delta functions present in the asymptotic expressions such as (B58) by $-1$![]() , and generalization of results from $\tau \in \mathbb {R}^+$
, and generalization of results from $\tau \in \mathbb {R}^+$![]() to $\tau \in \mathbb {R}$
to $\tau \in \mathbb {R}$![]() leads to a secularity in the limit $|\tau | \rightarrow \infty$
leads to a secularity in the limit $|\tau | \rightarrow \infty$![]() of the form
of the form
The resultant asymptotic expansion for $\tilde {h}^s(\boldsymbol {k},\tau )$![]() is therefore
is therefore
In what follows, we expand the leading-order behaviour of the two-time energy spectrum using the AP method and allow $\tilde {h}^s_{0,k}$![]() to vary on the lagged time scale $\varepsilon ^2 |\tau | = \tau _2$
to vary on the lagged time scale $\varepsilon ^2 |\tau | = \tau _2$![]() as
as
The choice of
removes the secularity and preserves the order of the asymptotic expansion for $\tilde {h}^s(\boldsymbol {k},\tau )$![]() . Equation (3.38) then provides the leading-order behaviour of $\tilde {h}^s(\boldsymbol {k},\tau )$
. Equation (3.38) then provides the leading-order behaviour of $\tilde {h}^s(\boldsymbol {k},\tau )$![]() through time lag $\tau =O(\varepsilon ^{-2})$
through time lag $\tau =O(\varepsilon ^{-2})$![]() in the form
in the form
Expression (3.39) can be integrated over wavevector $\boldsymbol {p}$![]() as well as $q_\parallel$
as well as $q_\parallel$![]() utilizing the delta function constraints in combination with $M^2_{k,pq}$
utilizing the delta function constraints in combination with $M^2_{k,pq}$![]() (see Appendix C) to obtain
(see Appendix C) to obtain

where
Equation (3.40) provides a first-order linear homogeneous ODE for the leading-order behaviour of the two-time energy spectrum in the interaction picture with the corresponding solution
for which
where we used the fact that the parallel correlation length can be defined as $2\lambda _{0\|}\equiv g^{-s}(0)$![]() . This decorrelation rate can be further simplified to gain more intuition about the nature of the decorrelation of weakly interacting Alfvén-wave fluctuations by seeking the change of variables $x\equiv q_\perp /k_\perp$
. This decorrelation rate can be further simplified to gain more intuition about the nature of the decorrelation of weakly interacting Alfvén-wave fluctuations by seeking the change of variables $x\equiv q_\perp /k_\perp$![]() , and assuming the spectra of fluctuations follow the power-law $\mathcal {E}^s(k_\perp )\propto k_\perp ^{-\alpha _s}$
, and assuming the spectra of fluctuations follow the power-law $\mathcal {E}^s(k_\perp )\propto k_\perp ^{-\alpha _s}$![]() , in which case it is straightforward to show that
, in which case it is straightforward to show that
From Galtier's weak turbulence closure it was found that the steady-state solutions of the WKE leads to $\alpha _+=\alpha _-=3$![]() in the balanced case, and it was argued by Boldyrev & Perez (Reference Boldyrev and Perez2009) that this is also the case in the imbalanced case. Based on these weak turbulence closures for the one-time spectra and dimensional arguments we assume that $\mathcal {E}^s(k_\perp )\sim v_0^2k_{0\perp }k_\perp ^{-3}$
in the balanced case, and it was argued by Boldyrev & Perez (Reference Boldyrev and Perez2009) that this is also the case in the imbalanced case. Based on these weak turbulence closures for the one-time spectra and dimensional arguments we assume that $\mathcal {E}^s(k_\perp )\sim v_0^2k_{0\perp }k_\perp ^{-3}$![]() , in which case we have
, in which case we have
where $\chi _0\equiv k_{0\perp } v_0/k_{0\|}v_{A}$![]() is the ratio of the nonlinear to the linear frequency at the outer scale, and indicative of the weakness of the turbulence which fluctuations of this size will experience. Hence for the regime of weak turbulence, $\chi _0 = O(\varepsilon )$
is the ratio of the nonlinear to the linear frequency at the outer scale, and indicative of the weakness of the turbulence which fluctuations of this size will experience. Hence for the regime of weak turbulence, $\chi _0 = O(\varepsilon )$![]() . The decorrelation frequency equation (3.45) then exhibits similar scaling (albeit exponential instead of a Gaussian functional dependence in $\tau$
. The decorrelation frequency equation (3.45) then exhibits similar scaling (albeit exponential instead of a Gaussian functional dependence in $\tau$![]() ) with the sweeping-based result obtained for strong turbulence by Bourouaine & Perez (Reference Bourouaine and Perez2019) and Perez & Bourouaine (Reference Perez and Bourouaine2020) in the form $k_\perp v_0$
) with the sweeping-based result obtained for strong turbulence by Bourouaine & Perez (Reference Bourouaine and Perez2019) and Perez & Bourouaine (Reference Perez and Bourouaine2020) in the form $k_\perp v_0$![]() . In addition to exhibiting different functional dependences, our result suggests that in the regime of weak turbulence, the strength of sweeping by the outer scale is reduced in proportion to the weakness of the turbulence in which this scale participates. This is made evident purely through the definition of $\chi _0$
. In addition to exhibiting different functional dependences, our result suggests that in the regime of weak turbulence, the strength of sweeping by the outer scale is reduced in proportion to the weakness of the turbulence in which this scale participates. This is made evident purely through the definition of $\chi _0$![]() . In the strong regime, $\chi _0 \geq O(1)$
. In the strong regime, $\chi _0 \geq O(1)$![]() ($\varepsilon$
($\varepsilon$![]() is no longer a small parameter) and the strong/weak decorrelation rates become comparable in order of magnitude, although this limit would largely invalidate the results presented herein. In the analysis performed by Bourouaine & Perez (Reference Bourouaine and Perez2019), it is assumed from the outset of computation that random sweeping by the outer scale is the dominant means of temporal decorrelation, and occurs much faster than linear Alfvénic propagation or nonlinear energy transfer. In contrast, the weak turbulence assumptions employed in this work mandate that Alfvénic propagation happens much faster than sweeping or nonlinear interaction. Despite the differing preliminary assumptions made regarding the separation between time scales governing the aforementioned physical processes, our calculation remarkably suggests a decorrelation characterized by sweeping with strength that is reduced in proportion to its disparity (in the form of $\chi _0$
is no longer a small parameter) and the strong/weak decorrelation rates become comparable in order of magnitude, although this limit would largely invalidate the results presented herein. In the analysis performed by Bourouaine & Perez (Reference Bourouaine and Perez2019), it is assumed from the outset of computation that random sweeping by the outer scale is the dominant means of temporal decorrelation, and occurs much faster than linear Alfvénic propagation or nonlinear energy transfer. In contrast, the weak turbulence assumptions employed in this work mandate that Alfvénic propagation happens much faster than sweeping or nonlinear interaction. Despite the differing preliminary assumptions made regarding the separation between time scales governing the aforementioned physical processes, our calculation remarkably suggests a decorrelation characterized by sweeping with strength that is reduced in proportion to its disparity (in the form of $\chi _0$![]() ) with the linear time scale. It is worth pointing out that this competition between sweeping and Alfvénic propagation at the outer scale requires additional investigation.
) with the linear time scale. It is worth pointing out that this competition between sweeping and Alfvénic propagation at the outer scale requires additional investigation.
Finally, noting definitions (2.12) and (3.3), the leading-order behaviour of the two-time energy spectrum may be expressed as
which implies a scale-dependent time correlation function of the form
Our solution (3.46) suggests oscillatory behaviour as well as exponential decay in the correlation between the temporally lagged states due to linear Alfvénic propagation and resonant nonlinear energy transfer, respectively. The former occurs on a time scale of order unity and is reminiscent of linear solutions to (2.7) while the latter becomes significant (keeping in mind $\gamma _k^s \sim k_\perp v_0 \chi _0 = O(\varepsilon t_{\rm nl}^{-1})$![]() ) at a temporal lag of $\tau =O(\varepsilon ^{-3}t_{\rm nl})$
) at a temporal lag of $\tau =O(\varepsilon ^{-3}t_{\rm nl})$![]() , an intermediary between $O(\varepsilon ^{-3})$
, an intermediary between $O(\varepsilon ^{-3})$![]() and $O(\varepsilon ^{-4})$
and $O(\varepsilon ^{-4})$![]() .
.
The conclusion of exponential decay becoming appreciable at a lag of $\tau =O(\varepsilon ^{-3}t_{\rm nl})$![]() appears to instigate a most interesting predicament, bringing into question the legitimacy of the underlying closure process. Calculations were performed to ensure uniformity of the two-time energy spectrum expansion equation (3.17) accurate through $O(\varepsilon ^2)$
appears to instigate a most interesting predicament, bringing into question the legitimacy of the underlying closure process. Calculations were performed to ensure uniformity of the two-time energy spectrum expansion equation (3.17) accurate through $O(\varepsilon ^2)$![]() in perturbation and correspondingly a time lag of $\tau = O(\varepsilon ^{-2})$
in perturbation and correspondingly a time lag of $\tau = O(\varepsilon ^{-2})$![]() , yet a result for $h_k^s(\tau )$
, yet a result for $h_k^s(\tau )$![]() is suggested herein which appears to exhibit perhaps the most significant aspect of its functional behaviour beyond the previously presumed domain of validity in $\tau$
is suggested herein which appears to exhibit perhaps the most significant aspect of its functional behaviour beyond the previously presumed domain of validity in $\tau$![]() . This apparent contradiction may possibly be readily rectified by § 5 of Benney & Newell (Reference Benney and Newell1969) (hereafter referred to as BN69) on higher closures.
. This apparent contradiction may possibly be readily rectified by § 5 of Benney & Newell (Reference Benney and Newell1969) (hereafter referred to as BN69) on higher closures.
For systems whose wave amplitudes evolve nonlinearly in time, generally speaking according to the form of BN69 (2.5), or more specifically for instance our (3.5), it is clearly demonstrated in § 5 of BN69 that genuine (as opposed to spurious) secularities in cumulant expansions arise at $O(\varepsilon ^2)$![]() and $O(\varepsilon ^4)$
and $O(\varepsilon ^4)$![]() in perturbation, while none are present at $O(\varepsilon ^3)$
in perturbation, while none are present at $O(\varepsilon ^3)$![]() as shown by the analysis leading to BN69 (5.3). Hence, removal of these secularities using the AP method is only necessary in their work on time scales of $T_2 = \varepsilon ^2 t$
as shown by the analysis leading to BN69 (5.3). Hence, removal of these secularities using the AP method is only necessary in their work on time scales of $T_2 = \varepsilon ^2 t$![]() and $T_4 = \varepsilon ^4 t$
and $T_4 = \varepsilon ^4 t$![]() . Correspondingly, the lower-order first-closure presented in our work only requires such corrections on lagged time scale $\tau _2 = \varepsilon ^2 \tau$
. Correspondingly, the lower-order first-closure presented in our work only requires such corrections on lagged time scale $\tau _2 = \varepsilon ^2 \tau$![]() as we are not concerned with $O(\varepsilon ^4)$
as we are not concerned with $O(\varepsilon ^4)$![]() behaviour. By direct mathematical analogy between the governing dynamical expressions of BN69 (2.5) and our own (3.5), a similar (albeit simpler, due to the quantity of interest being autocorrelation instead of energy) result is expected to follow, however, investigation of higher-order influence upon Fourier autocorrelation is well outside the scope of our own work.
behaviour. By direct mathematical analogy between the governing dynamical expressions of BN69 (2.5) and our own (3.5), a similar (albeit simpler, due to the quantity of interest being autocorrelation instead of energy) result is expected to follow, however, investigation of higher-order influence upon Fourier autocorrelation is well outside the scope of our own work.
Rigorous demonstration of the said absence of genuine secular growth in expansion (3.17) at $O(\varepsilon ^3)$![]() indeed requires a more complicated implementation of the AP method (see BN69 (3.3)) which contains a method for removing non-secular ‘free terms’ at lower orders in perturbation that otherwise lead to spurious closures (see BN69 (5.2)) at higher orders, including $O(\varepsilon ^{3})$
indeed requires a more complicated implementation of the AP method (see BN69 (3.3)) which contains a method for removing non-secular ‘free terms’ at lower orders in perturbation that otherwise lead to spurious closures (see BN69 (5.2)) at higher orders, including $O(\varepsilon ^{3})$![]() . Being that our own calculation is only interested in a first closure with accuracy to $O(\varepsilon ^2)$
. Being that our own calculation is only interested in a first closure with accuracy to $O(\varepsilon ^2)$![]() in perturbation, such a sophisticated analysis is unnecessary and not considered (Benney & Newell Reference Benney and Newell1969). Nonetheless, our calculation of (3.45) is likely rigorous through $O(\varepsilon ^3)$
in perturbation, such a sophisticated analysis is unnecessary and not considered (Benney & Newell Reference Benney and Newell1969). Nonetheless, our calculation of (3.45) is likely rigorous through $O(\varepsilon ^3)$![]() in perturbation insomuch as accounting for terms present in our expansion equation (3.17) which will exhibit genuine secular growth. This is admittedly speculative in nature, but nonetheless likely true because the closure calculations presented in both our work and BN69 exhibit similar underlying mathematical structure, despite the differences in functions of interest as well as the pertinent independent variable. Rigorous investigation and potential proof of such a claim in a more general form is likely to be part of future work on weak turbulence closures for Fourier autocorrelation. Should this claim turn out to be false, there is still inherent value in the results of what would prove to constitute but a semiphenomenological analysis. This is demonstrated through the conceptuality suggested by the functional forms of the two-time energy and power spectra described by (3.46) and (3.56) as they nonetheless allude to the lowest-non-trivial-order in perturbation influence of nonlinear resonant energy transfer upon two-point two-time statistics for the model employed herein. In light of this, we remind the reader that this is the same resonance responsible for closure and obtention of the well-known WKE result of Galtier et al. (Reference Galtier, Nazarenko, Newell and Pouquet2000) (or (B64) herein). Such simultaneity of causality begs the question: should a comparable ordering characterize the time scale over which spectral energy fluctuates?
in perturbation insomuch as accounting for terms present in our expansion equation (3.17) which will exhibit genuine secular growth. This is admittedly speculative in nature, but nonetheless likely true because the closure calculations presented in both our work and BN69 exhibit similar underlying mathematical structure, despite the differences in functions of interest as well as the pertinent independent variable. Rigorous investigation and potential proof of such a claim in a more general form is likely to be part of future work on weak turbulence closures for Fourier autocorrelation. Should this claim turn out to be false, there is still inherent value in the results of what would prove to constitute but a semiphenomenological analysis. This is demonstrated through the conceptuality suggested by the functional forms of the two-time energy and power spectra described by (3.46) and (3.56) as they nonetheless allude to the lowest-non-trivial-order in perturbation influence of nonlinear resonant energy transfer upon two-point two-time statistics for the model employed herein. In light of this, we remind the reader that this is the same resonance responsible for closure and obtention of the well-known WKE result of Galtier et al. (Reference Galtier, Nazarenko, Newell and Pouquet2000) (or (B64) herein). Such simultaneity of causality begs the question: should a comparable ordering characterize the time scale over which spectral energy fluctuates?
In fact, it is not difficult to show by means analogous to those which produced (3.44) and (3.45) an answer in the affirmative to this question. In Appendix D, it is demonstrated that the WKE
may be approximately recast in the form
Defining
(3.49) becomes the differential equation
with corresponding solution
Indeed, noting that $\varOmega _k^s \sim k_\perp v_0 \chi _0 = O(\varepsilon t_{\rm nl}^{-1})$![]() , the solution described by (3.52) suggests that energy fluctuates over a time scale $(\varepsilon ^2 \varOmega _k^s)^{-1} = O(\varepsilon ^{-3}t_{\rm nl})$
, the solution described by (3.52) suggests that energy fluctuates over a time scale $(\varepsilon ^2 \varOmega _k^s)^{-1} = O(\varepsilon ^{-3}t_{\rm nl})$![]() , as one may expect in the interest of phenomenological consistency (via common underlying causality) with the two-time energy spectrum equation (3.46). Again, we reference back to the concept demonstrated in BN69 that systems of this form only exhibit genuine secular behaviour on time scales of $O(\varepsilon ^{-2})$
, as one may expect in the interest of phenomenological consistency (via common underlying causality) with the two-time energy spectrum equation (3.46). Again, we reference back to the concept demonstrated in BN69 that systems of this form only exhibit genuine secular behaviour on time scales of $O(\varepsilon ^{-2})$![]() and $O(\varepsilon ^{-4})$
and $O(\varepsilon ^{-4})$![]() , and hence the WKE (3.48) as well as associated solution (3.52) are likely correct through the demonstrated relevant dynamical time scale $t=O(\varepsilon ^{-3}t_{\rm nl})$
, and hence the WKE (3.48) as well as associated solution (3.52) are likely correct through the demonstrated relevant dynamical time scale $t=O(\varepsilon ^{-3}t_{\rm nl})$![]() .
.
The property of exponential decay in correlation function equations (3.39) and (3.47) in the limit of large $\tau$![]() coincides with approximate solutions of a generic IDE for the SDTC derived and solved by Perez et al. (Reference Perez, Azelis and Bourouaine2020). The SDTC expression defined by (50) in that work is left in terms of an unspecified integral of the two-time energy spectrum, a function that is also not explicitly calculated by the authors. In contrast, our SDTC result (3.47) was extracted from a simple ODE and is dependent on parameters present in the RMHD model which are already fully determined at the outset of analytical computation. It is worth noting that the model of exponential decay has been proven applicable to the investigation of both simulation and spacecraft data (Matthaeus et al. Reference Matthaeus, Dasso, Weygand, Kivelson and Osman2010; Lugones et al. Reference Lugones, Dmitruk, Mininni, Wan and Matthaeus2016), however, the correct ${\mathrm e}$
coincides with approximate solutions of a generic IDE for the SDTC derived and solved by Perez et al. (Reference Perez, Azelis and Bourouaine2020). The SDTC expression defined by (50) in that work is left in terms of an unspecified integral of the two-time energy spectrum, a function that is also not explicitly calculated by the authors. In contrast, our SDTC result (3.47) was extracted from a simple ODE and is dependent on parameters present in the RMHD model which are already fully determined at the outset of analytical computation. It is worth noting that the model of exponential decay has been proven applicable to the investigation of both simulation and spacecraft data (Matthaeus et al. Reference Matthaeus, Dasso, Weygand, Kivelson and Osman2010; Lugones et al. Reference Lugones, Dmitruk, Mininni, Wan and Matthaeus2016), however, the correct ${\mathrm e}$![]() -folding time scale is obviously highly specific to the particular regime of turbulence being measured, assuming this functional form is even applicable to the relevant physical context under consideration.
-folding time scale is obviously highly specific to the particular regime of turbulence being measured, assuming this functional form is even applicable to the relevant physical context under consideration.
We can acquire an intuition for the result (3.46) by comparing (3.39) with the one-time result (B64). Equation (B64) suggests that the nonlinear energy flux into or out of a given mode with wavevector $\boldsymbol {k}$![]() after ‘scattering’ off a $\boldsymbol {q}_\perp$
after ‘scattering’ off a $\boldsymbol {q}_\perp$![]() mode is proportional to the difference in energy between itself and all possible waves of wavevector $\boldsymbol {p}$
mode is proportional to the difference in energy between itself and all possible waves of wavevector $\boldsymbol {p}$![]() capable of taking part in the interaction according to the delta function constraints. In contrast, (3.39) suggests that the signature of a given mode will decorrelate from itself in proportion to its own energy as well as that of all $\boldsymbol {q}_\perp$
capable of taking part in the interaction according to the delta function constraints. In contrast, (3.39) suggests that the signature of a given mode will decorrelate from itself in proportion to its own energy as well as that of all $\boldsymbol {q}_\perp$![]() modes with which it interacts. On time scales of $t=O(\varepsilon ^{-3} t_{\rm nl})$
modes with which it interacts. On time scales of $t=O(\varepsilon ^{-3} t_{\rm nl})$![]() , the energy $e^s_k$
, the energy $e^s_k$![]() of a mode will fluctuate according to (B64), but its statistical self-similarity $h^s_k$
of a mode will fluctuate according to (B64), but its statistical self-similarity $h^s_k$![]() , which evolves according to (3.39), will exponentially decay when the time lag $\tau$
, which evolves according to (3.39), will exponentially decay when the time lag $\tau$![]() separating the two instances at which the Elsasser field is evaluated approaches $O(\varepsilon ^{-3} t_{\rm nl})$
separating the two instances at which the Elsasser field is evaluated approaches $O(\varepsilon ^{-3} t_{\rm nl})$![]() . Given a sufficiently long time, the vectors in the complex plane representing the system's set of constituent Fourier modes will both rotate and change their norms. The overall state of the system will become entirely dissimilar from itself and there will no longer be a memory of the $\tau =0$
. Given a sufficiently long time, the vectors in the complex plane representing the system's set of constituent Fourier modes will both rotate and change their norms. The overall state of the system will become entirely dissimilar from itself and there will no longer be a memory of the $\tau =0$![]() field of turbulent fluctuations.
field of turbulent fluctuations.
The quantity $\gamma _k^s$![]() defines the rate at which the autocorrelation of a Fourier Elsasser mode with wavevector $\boldsymbol k$
defines the rate at which the autocorrelation of a Fourier Elsasser mode with wavevector $\boldsymbol k$![]() will exponentially decay via integration over all possible resonant nonlinear interactions in which it may partake during some temporal interval $\tau$
will exponentially decay via integration over all possible resonant nonlinear interactions in which it may partake during some temporal interval $\tau$![]() . The various mathematical features present in expression (3.43) provide phenomenological insight into the dynamical means by which a given mode will decorrelate from itself. Firstly, the prefactor $k_\perp ^2 / v_{A}$
. The various mathematical features present in expression (3.43) provide phenomenological insight into the dynamical means by which a given mode will decorrelate from itself. Firstly, the prefactor $k_\perp ^2 / v_{A}$![]() indicates that modes of smaller perpendicular spatial extent (higher $k_\perp$
indicates that modes of smaller perpendicular spatial extent (higher $k_\perp$![]() ) will decorrelate faster than larger ones. Additionally, inverse proportionality with the Alfvén velocity simply follows the intuition that counter-propagating waves will pass through each other more rapidly, weakening the strength of interaction. The predominant feature present in the decorrelation rate is an integration over the energy stored in the set of all non-propagating modes $\boldsymbol q= (q_\parallel = 0, \boldsymbol q_\perp )$
) will decorrelate faster than larger ones. Additionally, inverse proportionality with the Alfvén velocity simply follows the intuition that counter-propagating waves will pass through each other more rapidly, weakening the strength of interaction. The predominant feature present in the decorrelation rate is an integration over the energy stored in the set of all non-propagating modes $\boldsymbol q= (q_\parallel = 0, \boldsymbol q_\perp )$![]() with which $\boldsymbol k$
with which $\boldsymbol k$![]() interacts. The presence of the spectrum $g^{-s}(0)\mathcal {E}^{-s}(q_\perp )$
interacts. The presence of the spectrum $g^{-s}(0)\mathcal {E}^{-s}(q_\perp )$![]() merely suggests that the capacity for some turbulent grating $q_\perp$
merely suggests that the capacity for some turbulent grating $q_\perp$![]() to scatter $\boldsymbol k$
to scatter $\boldsymbol k$![]() is directly proportional to the stationary structure's energy content. Recalling the spectrum's inverse dependence on wavenumber, it can be inferred that modes with lower $q_\perp$
is directly proportional to the stationary structure's energy content. Recalling the spectrum's inverse dependence on wavenumber, it can be inferred that modes with lower $q_\perp$![]() scatter a given $\boldsymbol k$
scatter a given $\boldsymbol k$![]() with greater temporal efficiency. The spectral integral is modified by the presence of the function $\beta (q_\perp / k_\perp )$
with greater temporal efficiency. The spectral integral is modified by the presence of the function $\beta (q_\perp / k_\perp )$![]() , which provides a geometric weighting to the modal decorrelation rate dependent on the ratio of perpendicular wavenumbers of interacting modes. Rudimentary numerical integration suggests that this function is strongly peaked at $\beta (0)={\rm \pi} /2$
, which provides a geometric weighting to the modal decorrelation rate dependent on the ratio of perpendicular wavenumbers of interacting modes. Rudimentary numerical integration suggests that this function is strongly peaked at $\beta (0)={\rm \pi} /2$![]() and monotonically decays to an asymptotic value of $\beta \approx 0.2$
and monotonically decays to an asymptotic value of $\beta \approx 0.2$![]() for $q_\perp / k_\perp > 2$
for $q_\perp / k_\perp > 2$![]() . This functional behaviour reinforces the aforementioned concepts suggested by the numerator of the prefactor as well as the presence of the perpendicular spectrum that $q_\perp$
. This functional behaviour reinforces the aforementioned concepts suggested by the numerator of the prefactor as well as the presence of the perpendicular spectrum that $q_\perp$![]() modes of larger spatial expanse scatter $\boldsymbol k$
modes of larger spatial expanse scatter $\boldsymbol k$![]() modes with increased efficacy and the associated decorrelation is increasingly pronounced in proportion to $k_\perp$
modes with increased efficacy and the associated decorrelation is increasingly pronounced in proportion to $k_\perp$![]() . This is to suggest that in a field of turbulent fluctuations, larger structures are both more resistant to being scattered and distorted while simultaneously performing these actions onto others more effectively than those of smaller scale. It is worth noting that this may suggest the presence of energy transfer that is somewhat non-local in wavenumber space, but further investigation of this possibility is required and is well beyond the scope of the present analysis.
. This is to suggest that in a field of turbulent fluctuations, larger structures are both more resistant to being scattered and distorted while simultaneously performing these actions onto others more effectively than those of smaller scale. It is worth noting that this may suggest the presence of energy transfer that is somewhat non-local in wavenumber space, but further investigation of this possibility is required and is well beyond the scope of the present analysis.
When used in tandem with the Fourier transform expression (2.16), (3.46) has the potential to serve as an improvement over the TH in the regime of weakly turbulent MHD in the form of the space–time correlation function
where we have used $\boldsymbol r = z \hat {\boldsymbol {b}} + \boldsymbol r_\perp$![]() to isolate parallel from perpendicular correlation lengths and separated parallel and perpendicular spectra according to $e_{0,k}^{s}=\mathcal {E}^{s}(k_\perp )g^{s}(k_\|)$
to isolate parallel from perpendicular correlation lengths and separated parallel and perpendicular spectra according to $e_{0,k}^{s}=\mathcal {E}^{s}(k_\perp )g^{s}(k_\|)$![]() . If one assumes the existence of $G^{s}$
. If one assumes the existence of $G^{s}$![]() , the Fourier transform of $g^s$
, the Fourier transform of $g^s$![]() , integration with respect to $k_\parallel$
, integration with respect to $k_\parallel$![]() then yields the correlation
then yields the correlation
The parallel structure of the correlation $G^{s}$![]() contains a TH-like argument for an advecting flow travelling at the Alfvén velocity $v_{A}$
contains a TH-like argument for an advecting flow travelling at the Alfvén velocity $v_{A}$![]() in the $\pm \hat {\boldsymbol {b}}$
in the $\pm \hat {\boldsymbol {b}}$![]() direction and appears to be unaffected by the presence of nonlinear interactions. This is in agreement with observations of MHD turbulence simulations first made by Shebalin, Matthaeus & Montgomery (Reference Shebalin, Matthaeus and Montgomery1983) and forged to rigorous mathematical form in the WKE of Galtier et al. (Reference Galtier, Nazarenko, Newell and Pouquet2000); both of which describe spectral energy transfer that is highly anisotropic and confined to planes of constant $k_\parallel$
direction and appears to be unaffected by the presence of nonlinear interactions. This is in agreement with observations of MHD turbulence simulations first made by Shebalin, Matthaeus & Montgomery (Reference Shebalin, Matthaeus and Montgomery1983) and forged to rigorous mathematical form in the WKE of Galtier et al. (Reference Galtier, Nazarenko, Newell and Pouquet2000); both of which describe spectral energy transfer that is highly anisotropic and confined to planes of constant $k_\parallel$![]() . The said anisotropy is manifest in the $\boldsymbol {k}_\perp$
. The said anisotropy is manifest in the $\boldsymbol {k}_\perp$![]() integral in the form of resonant nonlinear energy transfer to higher $k_\perp$
integral in the form of resonant nonlinear energy transfer to higher $k_\perp$![]() , lending to exponential decay in the correlation as the dynamics proceed in time. Elsasser field autocorrelation unsurprisingly approaches zero as the perpendicular structure evolves into a different and unrecognizable version of itself due to turbulence. Contrary to the TH, (3.54) makes no assumption of frozen fluctuations while also taking into account the state of the plasma at multiple instances in time. As a result, the formulation provides an authentic two-point two-time correlation function with space and time independent, as opposed to the two-point one-time resulting from the aforementioned simplifications allotted by the TH. Additionally, further manipulation of (3.46) leads to a prediction of temporal frequency broadening due to the presence of nonlinear interactions.
, lending to exponential decay in the correlation as the dynamics proceed in time. Elsasser field autocorrelation unsurprisingly approaches zero as the perpendicular structure evolves into a different and unrecognizable version of itself due to turbulence. Contrary to the TH, (3.54) makes no assumption of frozen fluctuations while also taking into account the state of the plasma at multiple instances in time. As a result, the formulation provides an authentic two-point two-time correlation function with space and time independent, as opposed to the two-point one-time resulting from the aforementioned simplifications allotted by the TH. Additionally, further manipulation of (3.46) leads to a prediction of temporal frequency broadening due to the presence of nonlinear interactions.
If one first considers the temporal Fourier transform of the two-time energy spectrum equation (3.46) for the limit $\varepsilon = 0$![]() , such that there are no nonlinear interactions between fluctuations, the expression
, such that there are no nonlinear interactions between fluctuations, the expression
is obtained. The above result describes a delta function peaked about the Alfvén frequency $\omega = \omega ^s_k$![]() and coincides with a TH-based assumption for which the advecting fluid flow travels at the Alfvén velocity in either $s=\pm 1$
and coincides with a TH-based assumption for which the advecting fluid flow travels at the Alfvén velocity in either $s=\pm 1$![]() direction along the background magnetic field. Alternatively, it may be inferred that in the absence of nonlinear interactions, the temporal structure of the system can be directly predicted from the shear-Alfvénic dispersion relation and the signature of a fluctuation $s k_\parallel$
direction along the background magnetic field. Alternatively, it may be inferred that in the absence of nonlinear interactions, the temporal structure of the system can be directly predicted from the shear-Alfvénic dispersion relation and the signature of a fluctuation $s k_\parallel$![]() will only be sampled at a single unique frequency. In contrast, inclusion of nonlinear interactions leads to a temporal Fourier transform of (3.46) of the form
will only be sampled at a single unique frequency. In contrast, inclusion of nonlinear interactions leads to a temporal Fourier transform of (3.46) of the form
Equation (3.56) describes a power spectrum featuring Lorentzian peaks in the neighbourhood of $\omega = \omega _k^s$![]() that are both shifted away from pure linear Alfvénicity and appreciably broadened from infinitesimal width by the presence of the decorrelation frequency $\varepsilon ^2\gamma _k^s$
that are both shifted away from pure linear Alfvénicity and appreciably broadened from infinitesimal width by the presence of the decorrelation frequency $\varepsilon ^2\gamma _k^s$![]() . Exhibition of finite width indicates that interactions between fluctuations destroy the convenient, albeit superficial injective mapping between temporal and spatial structure allotted by the TH; a fluctuation with given $s k_\parallel$
. Exhibition of finite width indicates that interactions between fluctuations destroy the convenient, albeit superficial injective mapping between temporal and spatial structure allotted by the TH; a fluctuation with given $s k_\parallel$![]() will contribute to a continuum frequency band (as opposed to a single discrete delta function) in the system's power spectrum. While accurate interpretation of time-series measurements is made non-trivial by the presence of resonant nonlinear energy transfer, (3.56) attempts to make some prediction of expectation, at the very least in a qualitative manner.
will contribute to a continuum frequency band (as opposed to a single discrete delta function) in the system's power spectrum. While accurate interpretation of time-series measurements is made non-trivial by the presence of resonant nonlinear energy transfer, (3.56) attempts to make some prediction of expectation, at the very least in a qualitative manner.
4. Conclusion
A wave-turbulence closure was used to obtain a two-time power spectrum for weakly turbulent incompressible MHD. The resulting spectrum is (perhaps unsurprisingly) illustrative of spatiotemporal Alfvénic energy storage consistent with the fundamental tenet of time scale separation in wave turbulence. For short time lag of the order of the linear wave period, the autocorrelation associated with a given wavevector $\boldsymbol {k}$![]() will oscillate at a frequency reminiscent of linear propagation. At time lag $\tau = O(\varepsilon ^{-3} t_{\rm nl})$
will oscillate at a frequency reminiscent of linear propagation. At time lag $\tau = O(\varepsilon ^{-3} t_{\rm nl})$![]() , nonlinear energy transfer between counter-propagating waves results in an exponential decay proportional to the strength of the interactions. The decay rate of a given mode's autocorrelation was found to increase with perpendicular wavenumber. In addition, it was shown that a given turbulent mode's ability to decorrelate others is inversely proportional to its own perpendicular wavenumber. These relationships suggest that large-scale perpendicular structures require more time to decorrelate and also efface the plasma's memory of a given mode with greater temporal efficiency in contrast to higher wavenumber fluctuations.
, nonlinear energy transfer between counter-propagating waves results in an exponential decay proportional to the strength of the interactions. The decay rate of a given mode's autocorrelation was found to increase with perpendicular wavenumber. In addition, it was shown that a given turbulent mode's ability to decorrelate others is inversely proportional to its own perpendicular wavenumber. These relationships suggest that large-scale perpendicular structures require more time to decorrelate and also efface the plasma's memory of a given mode with greater temporal efficiency in contrast to higher wavenumber fluctuations.
While it has been shown that the majority of large-scale energy in the solar wind is in the form of Alfvénic fluctuations (Belcher & Davis Reference Belcher and Davis1971), the exact plasma regime which the Parker Solar Probe will encounter in the vicinity of perihelion is currently unknown. Nonetheless, an improved understanding of functions describing two-point two-time statistics will play a highly important role in the proper explication of Parker Solar Probe measurements as it traverses this region of space. There is hope that accurate interpretation and inferences made from the anticipated probe data will yield allusion to an explanation of the coronal heating problem that has eluded scientists for over 75 years.
Acknowledgements
The authors would like to thank the anonymous referees for their insightful questioning which led to improved presentation of this work.
Editor T. Passot thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Funding
A.A.A. was supported by US DOE grant DE-FG02-89ER53291. S.B. and J.C.P. were supported by NASA grants 80NSSC24K0137 and 80NSSC22K0518.
Appendix A. Derivation of (2.8)
In this section, a derivation of the fundamental expression (2.8) used throughout this work is presented. We begin with the governing equation of incompressible MHD in Elsasser form
The role of the diffusion terms is to merely act as a sink of energy for the turbulence cascade at very small scales where collisional dissipation takes place, resulting in plasma heating. Because the focus of this work is on the nonlinear cascade where dissipation is not important these terms will be ignored. In real systems such as the solar wind, other kinetic (collisionless, non-MHD) effects take over from which neither the cascade nor the dissipation can be described by the MHD approach. Analysis of the governing equations is initially performed in configuration (or real) space. As a result all quantities are defined at each point in space described by the three-dimensional position vector $\boldsymbol {x} \in \mathbb {R}^3$![]() . Equation (A1) can be recast as
. Equation (A1) can be recast as
where $\partial _\parallel = \hat {\boldsymbol {b}}\boldsymbol {\cdot }\boldsymbol {\nabla }$![]() and $s = +$
and $s = +$![]() or $-$
or $-$![]() is a compact notation for the Elsasser fields. Similar to incompressible fluid dynamics, the role of the pressure gradient is to enforce incompressibility. If the divergence operator is applied to (A2), one obtains in dyadic notation
is a compact notation for the Elsasser fields. Similar to incompressible fluid dynamics, the role of the pressure gradient is to enforce incompressibility. If the divergence operator is applied to (A2), one obtains in dyadic notation
whereupon inversion of the Laplacian provides an explicit formulation for $P$![]()
Substitution of (A4) into (A2) results in
The term in square brackets $[\delta _{ij} - \nabla ^{-2}\partial _i\partial _j] = P_{ij}(\boldsymbol {\nabla })$![]() is a projection operator which extracts the divergenceless or solenoidal part of a vector field
is a projection operator which extracts the divergenceless or solenoidal part of a vector field
For instance it is easily shown that $\partial _i (P_{ij}(\boldsymbol {\nabla }) u_j) = 0$![]()
In configuration space, the ideal incompressible MHD equation is then
Solution of (A8) is facilitated by use of the Fourier transform
The Fourier transform of (A8) is
Equation (A10) can be recast in vector form as
where
In this analysis, we are solely interested in the contribution to turbulence dynamics due to interactions between shear Alfvén waves. In incompressible MHD, the only modes present are the shear and pseudo-Alfvénic. The latter is a remnant of the slow magnetosonic wave which otherwise disappears in the incompressible limit. It was shown by Galtier & Chandran (Reference Galtier and Chandran2006) that the pseudo mode can be discarded at no penalty to the description of the dynamics. Both the wave and polarization vectors corresponding to the shear Alfvén mode are perpendicular to the direction of the background magnetic field $\hat {\boldsymbol {b}}$![]() . We can then create a coordinate system involving $\hat {\boldsymbol {b}}$
. We can then create a coordinate system involving $\hat {\boldsymbol {b}}$![]() , the perpendicular wavevector direction $\hat {\boldsymbol {k}}_\perp$
, the perpendicular wavevector direction $\hat {\boldsymbol {k}}_\perp$![]() , and the polarization vector $\hat {\boldsymbol {e}}_k$
, and the polarization vector $\hat {\boldsymbol {e}}_k$![]() of the shear mode such that
of the shear mode such that
The $\boldsymbol {z}^s(\boldsymbol {k},t)$![]() fields only have components along the $\hat {\boldsymbol {e}}_k$
fields only have components along the $\hat {\boldsymbol {e}}_k$![]() direction, therefore
direction, therefore
where $\phi ^s(\boldsymbol {k},t)$![]() is the scalar amplitude of the Elsasser field and the coefficient $\mathrm {i}$
is the scalar amplitude of the Elsasser field and the coefficient $\mathrm {i}$![]() is introduced to simplify subsequent calculations. The simplification provided by (A14) allows for the vector equation (A11) to be projected along the $-\mathrm {i}\hat {\boldsymbol {e}}_k$
is introduced to simplify subsequent calculations. The simplification provided by (A14) allows for the vector equation (A11) to be projected along the $-\mathrm {i}\hat {\boldsymbol {e}}_k$![]() direction and converted into a single scalar equation. Projecting each side of (A11), the time evolution of the amplitude $\phi ^s(\boldsymbol {k},t)$
direction and converted into a single scalar equation. Projecting each side of (A11), the time evolution of the amplitude $\phi ^s(\boldsymbol {k},t)$![]() of a shear Alfvén wave of wavevector $\boldsymbol {k}$
of a shear Alfvén wave of wavevector $\boldsymbol {k}$![]() is then given by
is then given by
We now seek to perform statistical analysis considering $\phi ^s(\boldsymbol {k},t)$![]() as a stochastic field to better understand the nature of weak turbulence in MHD. In anticipation of subsequent calculations, a new notation will be introduced which will make (A15) (and all quantities derived from it) more compact,
as a stochastic field to better understand the nature of weak turbulence in MHD. In anticipation of subsequent calculations, a new notation will be introduced which will make (A15) (and all quantities derived from it) more compact,

In this notation, (A15) becomes the desired result:
Appendix B. The RMHD WKE calculation using the AP method
In this appendix, we demonstrate the application of the AP method to incompressible MHD to derive a WKE originally found by Galtier et al. (Reference Galtier, Nazarenko, Newell and Pouquet2000). The intent is to educate the reader unfamiliar with weak turbulence closures of their typical use to derive WKEs and make clearer our methodology used in the main body of this work to find the alternative quantity, the Fourier Elsasser field autocorrelation or two-time energy spectrum. We present at a level of rigor necessary for the weak turbulence naïve to comprehend and reuse these methods for their own nonlinear wave equation. It is worth noting that a tutorial of weak turbulence theory for MHD is also presented in chapter 14 of Nazarenko (Reference Nazarenko2011).
Our presentation of the Galtier et al. (Reference Galtier, Nazarenko, Newell and Pouquet2000) derivation will begin from the starting point of Galtier et al. (Reference Galtier, Nazarenko, Newell and Pouquet2001) and Galtier & Chandran (Reference Galtier and Chandran2006), using the RMHD model for the Fourier shear-Alfvén amplitudes given by (2.8). However, our method of statistical closure follows the AP method which was first developed in Benney & Newell (Reference Benney and Newell1967, Reference Benney and Newell1969). This particular method of weak turbulence closure consists of developing dynamical equations for the second- and third-order cumulants, naïvely perturbing the statistical cumulant hierarchy, and renormalizing the expansion to remove secular terms in a manner that simultaneously yields the desired WKE.
The general procedure for this method begins with the development of a hierarchy of dynamical equations for the cumulants of the Fourier wave amplitudes from the governing equation (B3). Cumulants are specific combinations of statistical moments describing a given system's departure from a state of Gaussianity; Gaussian fields with zero mean possess the feature that all cumulants above second order are identically zero. They are generally preferred over moments because they possess the property of vanishing as the separation between two points becomes infinitely large ($|\boldsymbol {r}|\rightarrow \infty$![]() ), implying that they are $L^1$
), implying that they are $L^1$![]() functions, i.e. norm integrable over the entire configuration (or physical) space. This is of fundamental importance in the ensuing analysis because it suggests the existence of the cumulants’ Fourier transforms as regular (rather than generalized) functions, which in general is not guaranteed for the moments (Batchelor Reference Batchelor1999). Because we assume the wave amplitudes to have zero average, the second- and third-order moments coincide with their corresponding cumulant. For this reason, hereafter we refer to the second- and third-order moments as cumulants.
functions, i.e. norm integrable over the entire configuration (or physical) space. This is of fundamental importance in the ensuing analysis because it suggests the existence of the cumulants’ Fourier transforms as regular (rather than generalized) functions, which in general is not guaranteed for the moments (Batchelor Reference Batchelor1999). Because we assume the wave amplitudes to have zero average, the second- and third-order moments coincide with their corresponding cumulant. For this reason, hereafter we refer to the second- and third-order moments as cumulants.
The hierarchy is developed to obtain dynamical equations describing the temporal evolution of the second- and third-order cumulants $e^s_k(t)$![]() and $Q^{(s,s,-s)(3)}_{kp}(t)\equiv Q^{(s,s,-s)(3)}(\boldsymbol k,\boldsymbol p,t)$
and $Q^{(s,s,-s)(3)}_{kp}(t)\equiv Q^{(s,s,-s)(3)}(\boldsymbol k,\boldsymbol p,t)$![]() :
:
where the Dirac deltas are due to spatial homogeneity.
The second- to fourth-order cumulants present in the resulting dynamical equations are then asymptotically expanded in terms of a small parameter $\varepsilon$![]() , characterizing the relative strength of nonlinear versus linear terms over the system's temporal evolution. The resulting system of equations is solved recursively to order $\varepsilon ^2$
, characterizing the relative strength of nonlinear versus linear terms over the system's temporal evolution. The resulting system of equations is solved recursively to order $\varepsilon ^2$![]() in perturbation and the asymptotic behaviour of these solutions, when $t\rightarrow \infty$
in perturbation and the asymptotic behaviour of these solutions, when $t\rightarrow \infty$![]() with $\varepsilon ^2t\sim 1$
with $\varepsilon ^2t\sim 1$![]() , is investigated.
, is investigated.
The asymptotic analysis divides solutions into two classes of functions based on their long-time behaviour, a procedure that is more transparent in the interaction representation
In this representation, the field $\psi ^s_{k}(t)$![]() describes the slow temporal evolution due to weak nonlinearities, while the exponential term explicitly accounts for wave oscillations at the Alfvén frequency $\omega ^s_k=sk_\|v_{A}$
describes the slow temporal evolution due to weak nonlinearities, while the exponential term explicitly accounts for wave oscillations at the Alfvén frequency $\omega ^s_k=sk_\|v_{A}$![]() . In this description, the dynamical equations for the slowly evolving amplitudes $\psi ^s_{k}(t)$
. In this description, the dynamical equations for the slowly evolving amplitudes $\psi ^s_{k}(t)$![]() follow from (2.8):
follow from (2.8):
While the second-order cumulant is the same in both representations,
the third-order cumulant becomes
Defining the slowly varying third-order cumulant (in terms of $\psi ^s_{k}(t)$![]() ) as
) as
we have

Comparing the third-order cumulant from (B1a,b) with (B7), it follows that
It will be shown that the majority of terms in the asymptotic expansion lack explicit time dependence in the long-time limit and are deemed ‘non-secular’. In contrast, other terms will arise containing the said dependence which correspond to resonances and are referred to as secular. Functions in the latter group may grow without bound in the long-time limit, disrupting the order of the asymptotic expansion. Generally speaking, secularities result in higher-order terms becoming larger than lower-order ones, an obvious contradiction to the notion of a regular perturbative solution. Despite appearing to preclude any hope of a solution, it is precisely the presence of secularities that allows for the closure of the cumulant hierarchy. The asymptotic expansion for the second-order cumulant is reordered according to the secularity using the AP method as
and the behaviour of the energy spectrum equation (2.12) is found through times of $O(\varepsilon ^{-2})$![]() .
.
B.1 Development of one-time hierarchy
In this subsection, dynamical equations for second- and third-order cumulant growth are found. These expressions are sought with the intent of eventually performing asymptotic expansions in the first few functions of the cumulant hierarchy and a subsequent search for the occurrence of secular terms. Equation (B4) is the starting point for the development of the said hierarchy. Differentiation with respect to time on both sides of (B4), in combination with (B3), yields

where $\mathcal {P}_{sk,sk'}$![]() is a permutation operator that creates two terms arising from the two possible combinations of $sk,sk'$
is a permutation operator that creates two terms arising from the two possible combinations of $sk,sk'$![]() . As expected from the well-known statistical closure problem in which temporal evolution of the $n$
. As expected from the well-known statistical closure problem in which temporal evolution of the $n$![]() th-order cumulant depends on the ($n$
th-order cumulant depends on the ($n$![]() +1)th, the dynamical equation for the second-order cumulant $\langle \psi ^s_{k}(t)\psi ^s_{k'}(t) \rangle$
+1)th, the dynamical equation for the second-order cumulant $\langle \psi ^s_{k}(t)\psi ^s_{k'}(t) \rangle$![]() is determined by the third-order cumulant $\langle \psi ^s_{p}(t)\psi ^{-s}_{q}(t)\psi ^s_{k'}(t) \rangle$
is determined by the third-order cumulant $\langle \psi ^s_{p}(t)\psi ^{-s}_{q}(t)\psi ^s_{k'}(t) \rangle$![]() . After simple manipulations, (B4), (B6) and (B10) yield the following evolution equation for the energy spectrum:
. After simple manipulations, (B4), (B6) and (B10) yield the following evolution equation for the energy spectrum:
in terms of the third-order cumulant associated with $\psi ^s_{k}(t)$![]() , which is responsible for the energy transfer among modes in a given triad. By virtue of the closure problem we now require an equation for the third-order cumulant $\tilde Q^{(s,s,-s)(3)}_{-kp}(t).$
, which is responsible for the energy transfer among modes in a given triad. By virtue of the closure problem we now require an equation for the third-order cumulant $\tilde Q^{(s,s,-s)(3)}_{-kp}(t).$![]() Differentiating equation (B6) with respect to time we obtain
Differentiating equation (B6) with respect to time we obtain

Not surprisingly, the evolution of the third-order cumulant $\langle \psi ^s_{k}(t)\psi ^s_{p}(t)\psi ^{-s}_{q}(t) \rangle$![]() is determined by the fourth-order moment $\langle \psi ^s_{l}(t) \psi ^{-s}_{n}(t)\psi ^s_{p}(t)\psi ^{-s}_{q}(t) \rangle$
is determined by the fourth-order moment $\langle \psi ^s_{l}(t) \psi ^{-s}_{n}(t)\psi ^s_{p}(t)\psi ^{-s}_{q}(t) \rangle$![]() . The temporal evolution of the third-order cumulant is sought via
. The temporal evolution of the third-order cumulant is sought via

The fourth-order cumulant denoted by curly brackets, is related to the fourth-order moment and products of second-order moments

Noting the simplifications allotted by (B4) as well as the random phase (resulting in null correlation) between counter-propagating waves, the fourth-order moment is then expressed as
Via (B4) and (B15), (B13) simplifies to

Terms containing the energy spectrum in (B16) may be integrated resulting in

where we have used the fact that $M_{{k},{p}{q}} = -M_{{p},{k}{q}}$![]() . The terms containing the fourth-order cumulant can be contracted with the permutation operator
. The terms containing the fourth-order cumulant can be contracted with the permutation operator

The evolution of the third-order cumulant given by (B13) can expressed as

Noting that (B11) contains a third-order cumulant of the form $\tilde {Q}^{(s,s,-s)(3)}_{-kp}(t)$![]() , (B19) is recast as
, (B19) is recast as

In the following subsection, we asymptotically expand the second- to fourth-order cumulants of (B11) and (B20) to order $\varepsilon ^2$![]() . The long-time ($t\rightarrow \infty$
. The long-time ($t\rightarrow \infty$![]() ) behaviour of the equations at the various orders is then investigated and renormalization of the expansion (B21) by the method (B9) yields a dynamical expression for the energy spectrum (B4).
) behaviour of the equations at the various orders is then investigated and renormalization of the expansion (B21) by the method (B9) yields a dynamical expression for the energy spectrum (B4).
B.2 Weak turbulence closure for the energy spectrum
In this subsection, the previously derived dynamical equations (B11) and (B20) are subject to cumulant expansions in parameter $\varepsilon$![]() . What follows is a series of explicit time integrations of the expanded system of equations which may lead to secular terms. The renormalization (B9) is used to remove secularities, resulting in (B64).
. What follows is a series of explicit time integrations of the expanded system of equations which may lead to secular terms. The renormalization (B9) is used to remove secularities, resulting in (B64).
Equations (B11) and (B20) are approximately solved via the asymptotic expansions
to obtain the leading-order time dependence of the energy spectrum through time scale $t=O(\varepsilon ^{-2})$![]() . Substituting equations (B21)–(B23) and equating terms by order in $\varepsilon$
. Substituting equations (B21)–(B23) and equating terms by order in $\varepsilon$![]() results in the system of equations
results in the system of equations

subject to the following initial conditions:
Due to the closure problem, (B24)–(B28) represent an incomplete set of equations describing only the second- and third-order cumulant, to second and first order in $\varepsilon$![]() , respectively. Equations (B24) and (B25) imply that to zero order in $\varepsilon$
, respectively. Equations (B24) and (B25) imply that to zero order in $\varepsilon$![]() the energy spectrum $e^s_{0,k}(t)$
the energy spectrum $e^s_{0,k}(t)$![]() and third-order cumulant $\tilde Q^{(s,s,-s)(3)}_{0,-kp}(t)$
and third-order cumulant $\tilde Q^{(s,s,-s)(3)}_{0,-kp}(t)$![]() are constant with respect to time, and from the initial conditions it immediately follows that
are constant with respect to time, and from the initial conditions it immediately follows that
As a result, (B25) and (B27) may be directly integrated as the only time dependence on their right-hand sides are due to the complex exponentials. In anticipation of the forms of the integrals that follow at higher order, we will define a series of functions that occur repeatedly in the closure process. We are interested in the long-time behaviour $(t\rightarrow \infty )$![]() of these functions (Benney & Newell Reference Benney and Newell1969), while making sure we maintain the order of the asymptotic expansion equation (B21). To begin, we evoke the Riemann–Lebesgue lemma which states that if $f(x)$
of these functions (Benney & Newell Reference Benney and Newell1969), while making sure we maintain the order of the asymptotic expansion equation (B21). To begin, we evoke the Riemann–Lebesgue lemma which states that if $f(x)$![]() is a function in $L^1$
is a function in $L^1$![]() (see for instance Stein & Shakarchi Reference Stein and Shakarchi2011) such that
(see for instance Stein & Shakarchi Reference Stein and Shakarchi2011) such that
then
Furthermore, if $f(x)$![]() satisfies Dirichlet's conditions, then
satisfies Dirichlet's conditions, then
and a stronger condition is imposed upon the asymptotic behaviour of the integral (Davies Reference Davies2002). These results are of vital importance for the success of the wave-turbulence closure, which separates cumulant evolution into two different processes. Because of linear wave propagation, all initial cumulants higher than second order are multiplied by a fast non-vanishing oscillation term and will decay on the linear wave period time scale $(v_{A} k_\parallel )^{-1}=O(t^{-1})$![]() due to the Riemann–Lebesgue lemma (B34). This process results in the statistics of the system having a tendency to approach a state of Gaussianity. The extent of discrepancy with this state is described by the second process in which the system's waves will nonlinearly interact and exchange energy on time scale $\varepsilon ^{-2}$
due to the Riemann–Lebesgue lemma (B34). This process results in the statistics of the system having a tendency to approach a state of Gaussianity. The extent of discrepancy with this state is described by the second process in which the system's waves will nonlinearly interact and exchange energy on time scale $\varepsilon ^{-2}$![]() , regenerating the third- and higher-order cumulants (Benney & Newell Reference Benney and Newell1969; Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000).
, regenerating the third- and higher-order cumulants (Benney & Newell Reference Benney and Newell1969; Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000).
These properties of the closure process may be directly observed by considering the behaviour of the cumulants in configuration space. For each cumulant in the statistical hierarchy, there is a corresponding spatial correlation function which may be obtained via a Fourier transform. For instance, the second-order cumulant, otherwise known as the energy spectrum corresponds to a two-point correlation function
Similarly, the third-order cumulant corresponds to a three-point correlation function of the form
Due to the interaction representation, a new feature arises at this statistical order in the form of a complex exponential. It is observed that (B38) contains an integral of the form
which will in general cause terms in the expansion (B22) to decay via the Riemann–Lebesgue lemma. Exemptions from this decay will occur for terms in the expansion (B22) for which the complex exponential in (B39) is exactly cancelled. These vanishing complex phases correspond to resonant interactions between triads of waves and lead to secular behaviour in the energy spectrum. Continuing in increasing statistical order, the fourth-order cumulant has a configuration space counterpart of the form

The singular perturbative analysis performed in this work only seeks to calculate the one- and two-time energy spectra correct to order $\varepsilon ^2$![]() . Because of the time scale separation between linear and nonlinear processes imposed by the ordering parameter $\varepsilon$
. Because of the time scale separation between linear and nonlinear processes imposed by the ordering parameter $\varepsilon$![]() in confluence with the fundamental nature of the statistical closure problem, the evolution of the $m$
in confluence with the fundamental nature of the statistical closure problem, the evolution of the $m$![]() th-(statistical)-order cumulant at order $\varepsilon ^n$
th-(statistical)-order cumulant at order $\varepsilon ^n$![]() depends on the $m+1$
depends on the $m+1$![]() th-order cumulant at order $\varepsilon ^{n-1}$
th-order cumulant at order $\varepsilon ^{n-1}$![]() . Consequentially, all terms in cumulant expansions (B21)–(B23) of $O(\varepsilon ^0)$
. Consequentially, all terms in cumulant expansions (B21)–(B23) of $O(\varepsilon ^0)$![]() are constants. The aforementioned notions are directly observed in the structure of the hierarchy of (B24)–(B28). Therefore, to describe behaviour of the energy spectrum correct to $O(\varepsilon ^2)$
are constants. The aforementioned notions are directly observed in the structure of the hierarchy of (B24)–(B28). Therefore, to describe behaviour of the energy spectrum correct to $O(\varepsilon ^2)$![]() , we only require knowledge of fourth-order cumulant $Q^{(s,s,-s,-s)(4)}_{plq}(t)$
, we only require knowledge of fourth-order cumulant $Q^{(s,s,-s,-s)(4)}_{plq}(t)$![]() to $O(\varepsilon ^0)$
to $O(\varepsilon ^0)$![]() as described by the time independent constant $\tilde Q_{0,plq}^{(s,s,-s,-s)(4)}$
as described by the time independent constant $\tilde Q_{0,plq}^{(s,s,-s,-s)(4)}$![]() . Within the scope of this perturbative analysis, the fourth-order cumulant will behave in configuration space according to
. Within the scope of this perturbative analysis, the fourth-order cumulant will behave in configuration space according to

This four-point correlation contains an integral of the form
and will result in (B41) decaying via the Riemann–Lebesgue lemma. This decay results in the closure of the cumulant hierarchy through $O(\varepsilon ^2)$![]() as the need for a dynamical equation describing $\tilde Q_{0,plq}^{(s,s,-s,-s)(4)}$
as the need for a dynamical equation describing $\tilde Q_{0,plq}^{(s,s,-s,-s)(4)}$![]() is eliminated by the combination of linear wave propagation and time scale separation. The necessity of equations describing fifth- and higher-order cumulants is removed and what remains is a singular perturbative analysis of the (B26)–(B28).
is eliminated by the combination of linear wave propagation and time scale separation. The necessity of equations describing fifth- and higher-order cumulants is removed and what remains is a singular perturbative analysis of the (B26)–(B28).
The next function that will be encountered in the analysis of the perturbed hierarchy is of the form
In a functional sense, $\varDelta _t(x)$![]() acts on a sufficiently well-behaved function $f(x)$
acts on a sufficiently well-behaved function $f(x)$![]() in the long-time limit as
in the long-time limit as
which is expressed in an operational sense as
where $\sim$![]() denotes $\lim _{t\rightarrow \infty }$
denotes $\lim _{t\rightarrow \infty }$![]() and $P(1/x)$
and $P(1/x)$![]() is the Cauchy principal value distribution. For a non-zero constant $m$
is the Cauchy principal value distribution. For a non-zero constant $m$![]() , the corresponding asymptotic behaviour is
, the corresponding asymptotic behaviour is
The results of (B44) and (B45) may be calculated via contour integration and the function $\varDelta _t(mx)$![]() is observed to be well-behaved (non-secular) in the limit of large time. Direct integration of (B26) and (B27) while noting the resulting terms of the form $\varDelta _t(mx)$
is observed to be well-behaved (non-secular) in the limit of large time. Direct integration of (B26) and (B27) while noting the resulting terms of the form $\varDelta _t(mx)$![]() yields
yields

The only time dependence in (B47) and (B48) is due to functions of the form $\varDelta _t(mx)$![]() . These functions are non-secular and therefore it implies that the expansions (B21) and (B22) are well ordered in time to first order in $\varepsilon$
. These functions are non-secular and therefore it implies that the expansions (B21) and (B22) are well ordered in time to first order in $\varepsilon$![]() . While seemingly innocuous, the first term in (B48) has far-reaching implications for the three-point correlation function (B38) and second-order energy spectrum equation (B28). Substitution of (B48) into (B38) yields
. While seemingly innocuous, the first term in (B48) has far-reaching implications for the three-point correlation function (B38) and second-order energy spectrum equation (B28). Substitution of (B48) into (B38) yields

The product of $\varDelta _t(-2\omega _n^s)$![]() and complex exponential in the second term of (B49) yields a function of the form
and complex exponential in the second term of (B49) yields a function of the form
and results in decay via the Riemann–Lebesgue lemma. The first term of (B49), however, contains a term for which the complex exponential phases exactly cancel

and lends to the three-point correlation function containing a resonant term
that does not decay via the Riemann–Lebegue lemma. It is precisely the presence of this resonant term that will lead to secular behaviour in the $O(\varepsilon ^2)$![]() energy spectrum evolution and yield solubility of the singular perturbation problem.
energy spectrum evolution and yield solubility of the singular perturbation problem.
Substitution of (B48) into (B28) followed by integration with respect to time results in

We now must evaluate the long-time behaviour of each of the integrals with respect to $t'$![]() present in (B53). It can be shown that the first integral may be rewritten as
present in (B53). It can be shown that the first integral may be rewritten as
while the second is recast in the form
The integrals (B54) and (B55) are of the respective forms
and
These integrals exhibit the corresponding asymptotic behaviour
Via (B45), it is clear that (B59) is well-behaved for all time. In contrast, (B58) contains a linear dependence in $t$![]() . As a result, the asymptotic expansion (B21) will cease to be well ordered for times $t = O( \varepsilon ^{-2})$
. As a result, the asymptotic expansion (B21) will cease to be well ordered for times $t = O( \varepsilon ^{-2})$![]() . Due to only considering the real part of (B54) in (B53), there will be development of a secular term of the form
. Due to only considering the real part of (B54) in (B53), there will be development of a secular term of the form
We have found an asymptotic expansion for the power spectrum of the form (B21)
however, it ceases to be well ordered at time $t = O(\varepsilon ^{-2})$![]() .
.
Using the AP method, the spectrum may be reordered according to
The choice of
removes the secularity and reorders the asymptotic expansion for the time-dependent power spectrum, resulting in a closure accurate to order $\varepsilon ^2$![]() . Noting that $T_2 = \varepsilon ^2 t$
. Noting that $T_2 = \varepsilon ^2 t$![]() is an artificial time scale, the temporal evolution of the wavenumber energy spectrum can be expressed as
is an artificial time scale, the temporal evolution of the wavenumber energy spectrum can be expressed as
The factor of $\delta (q_\parallel )$![]() in (B64) in combination with $\delta _{k,pq}$
in (B64) in combination with $\delta _{k,pq}$![]() implies that energy transfer only occurs between waves with the same parallel wavenumber $k_\parallel =p_\parallel$
implies that energy transfer only occurs between waves with the same parallel wavenumber $k_\parallel =p_\parallel$![]() . Consequently, the three wave interactions can be interpreted as analogous to Bragg scattering of waves with non-zero $k_\parallel$
. Consequently, the three wave interactions can be interpreted as analogous to Bragg scattering of waves with non-zero $k_\parallel$![]() off of a ‘two-dimensional turbulent grating’ made of $q_\parallel = 0$
off of a ‘two-dimensional turbulent grating’ made of $q_\parallel = 0$![]() modes (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2002). In addition, this implies that each $k_\parallel$
modes (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2002). In addition, this implies that each $k_\parallel$![]() plane will evolve independently and the parallel spatial structure of the turbulence is time invariant. This permits the energy spectrum to be expressed as $e^s(\boldsymbol {k})=\mathcal {E}^s(k_\perp )g^s(k_\|)$
plane will evolve independently and the parallel spatial structure of the turbulence is time invariant. This permits the energy spectrum to be expressed as $e^s(\boldsymbol {k})=\mathcal {E}^s(k_\perp )g^s(k_\|)$![]() such that $\mathcal {E}^s(k_\perp )$
such that $\mathcal {E}^s(k_\perp )$![]() describes the perpendicular energy spectrum and $g^s(k_\|)$
describes the perpendicular energy spectrum and $g^s(k_\|)$![]() is a non-universal function suggesting the energy distribution among the field-parallel component of waves (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000). Closure was made possible due to the cumulant evolution separating into two different time scales. The first of these time scales coincides with linear propagation while the second is associated with nonlinear interactions and energy transfer between counter-propagating waves. In correspondence with the former, at order $\varepsilon ^0$
is a non-universal function suggesting the energy distribution among the field-parallel component of waves (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000). Closure was made possible due to the cumulant evolution separating into two different time scales. The first of these time scales coincides with linear propagation while the second is associated with nonlinear interactions and energy transfer between counter-propagating waves. In correspondence with the former, at order $\varepsilon ^0$![]() in time, the system tends towards a state of joint Gaussianity, as indicated by the time-invariant zero-order energy spectrum. This is reminiscent of the tendency of a system behaving under the central limit theorem. Over the second time scale of $\varepsilon ^2 t$
in time, the system tends towards a state of joint Gaussianity, as indicated by the time-invariant zero-order energy spectrum. This is reminiscent of the tendency of a system behaving under the central limit theorem. Over the second time scale of $\varepsilon ^2 t$![]() , nonlinear couplings between waves regenerate the non-Gaussian components of the Elsasser field statistics. Because of the difference in order of these processes, the zero-order fields can be non-rigorously assumed Gaussian without discarding information about the system (Benney & Saffman Reference Benney and Saffman1966).
, nonlinear couplings between waves regenerate the non-Gaussian components of the Elsasser field statistics. Because of the difference in order of these processes, the zero-order fields can be non-rigorously assumed Gaussian without discarding information about the system (Benney & Saffman Reference Benney and Saffman1966).
Appendix C. Simplification of (3.39)
In this section, the wavevector integrals of (3.39) are performed in order to reduce the ODE to a simpler form. The integral on the right-hand side of (3.39) can be expanded as
Integration over $\boldsymbol {p}$![]() subject to the delta function constraint $\delta _{k,pq}$
subject to the delta function constraint $\delta _{k,pq}$![]() results in
results in

Using a volume element ${\mathrm d}\boldsymbol {q} = q_\perp {\mathrm d} q_\perp {\mathrm d}\phi {\mathrm d}q_\parallel$![]() , choosing the coordinate system's angle $\phi$
, choosing the coordinate system's angle $\phi$![]() to coincide with the angle between $\boldsymbol {q}_\perp$
to coincide with the angle between $\boldsymbol {q}_\perp$![]() and $\boldsymbol {k}_\perp$
and $\boldsymbol {k}_\perp$![]() and separating the energy spectrum into perpendicular and parallel spectra according to $e_{0,q}^{-s}=\mathcal {E}^{-s}(q_\perp )g^{-s}(q_\|),$
and separating the energy spectrum into perpendicular and parallel spectra according to $e_{0,q}^{-s}=\mathcal {E}^{-s}(q_\perp )g^{-s}(q_\|),$![]() we obtain
we obtain

Integration over $q_\parallel$![]() and further algebraic manipulation yields a result for the integral on the right-hand side of (3.39)
and further algebraic manipulation yields a result for the integral on the right-hand side of (3.39)
where
Substitution of (C4) back into (3.39) yields the result (3.40):

Appendix D. Simplification of WKE (B64)
In this section, the WKE for weakly turbulent incompressible MHD
is manipulated in a manner similar to the procedure described by the mathematical progression from (3.39)–(3.46) in order to characterize a functional form for temporal energy fluctuations and infer the ordering of an associated characteristic time scale. The second term under the integral of (D1) may be simplified in a manner comparable to Appendix C as

Employing spectral scaling $\mathcal {E}^s(k_\perp ) \propto k_\perp ^{-\alpha _s}$![]() in conjunction with the change of variables $x\equiv q_\perp /k_\perp$
in conjunction with the change of variables $x\equiv q_\perp /k_\perp$![]() , we obtain
, we obtain
Following similar logic, the first term under the integral of (D1) can be manipulated to the form

Reintroducing the results of (D3) and (D4) into (D1), a differential equation is obtained of the form
Lastly, evoking the scaling $\mathcal {E}^{-s}(k_\perp ) \sim v_0^2k_{0\perp }k_\perp ^{-3}$![]() , (D5) becomes
, (D5) becomes