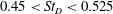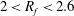The bifurcation and the blooming of jets have been numerically investigated at moderate Reynolds numbers. The study is motivated by a review article of Reynolds et al. (Annu. Rev. Fluid Mech., vol. 35, 2003, pp. 295–315) in which flow visualization images of jet blooming have been discussed, when the flow is subjected to inflow perturbations. Dual-mode perturbation, a combination of axisymmetric and helical excitations, has been used at the inflow plane to control the jet structures. In addition to the excitation frequency ratio, the effects of small-scale perturbation, excitation amplitude and initial momentum thickness have been examined. Results obtained at a Reynolds number of 2000 show that the number of branches formed in the blooming jet is strongly dependent on the excitation frequency ratio. For frequency ratios of 2, 2.5, 2.25, 2.4 and 2.22, the number of branches seen is 2, 5, 9, 12 and 20 respectively. In a blooming jet, the offset angle lies in the range 140°–180°. An equal number of branches is seen in the time-averaged flow field as well. The range of excitation frequency of the axisymmetric mode of perturbation is found to be 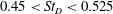$0.45<\mathit{St}_{D}<0.525$, with an excitation frequency ratio range of 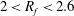$2<R_{f}<2.6$, for which blooming jets are formed. The role of inlet shear layer thickness is less important as far as the blooming jet is concerned, while increasing excitation amplitude increases entrainment. Time-averaged data show that the blooming patterns persist in time, showing a substantial increase in spreading and entrainment.

We present direct numerical simulations of decaying magnetohydrodynamic (MHD) turbulence at low magnetic Reynolds number. The domain considered is bounded by periodic boundary conditions in the two directions perpendicular to the magnetic field and by two plane Hartmann walls in the third direction. Regimes of high magnetic fields (Hartmann number of up to 896) are reached thanks to a new spectral method using the eigenvectors of the dissipation operator. The decay is found to proceed through two phases: first, energy and integral length scales vary rapidly during a two-dimensionalisation phase extending over approximately a Hartmann friction time. During this phase, the evolution of the former appears significantly more impeded by the presence of walls than that of the latter. Once the large scales are nearly quasi-two-dimensional, the decay results from the competition of a two-dimensional dynamics driven by dissipation in the Hartmann boundary layers and the three-dimensional dynamics of smaller scales. In the later stages of the decay, three-dimensionality subsists under the form of barrel-shaped structures. A purely quasi-two dimensional decay entirely dominated by friction in the Hartmann layers is not reached because of residual dissipation in the bulk. However, this dissipation is not generated by the three-dimensionality that subsists, but by residual viscous friction due to horizontal velocity gradients. In the process, the energy in the velocity component aligned with the magnetic field is found to be strongly suppressed, as is skewness. This result reproduces the experimental findings of Kolesnikov & Tsinober (Fluid Dyn., vol. 9, 1974, pp. 621–624), where, as in the present simulations, Hartmann walls were present.

Backwater curves denote the depth profiles of steady flows in a shallow open channel. The classification of these curves for turbulent regimes is commonly used in hydraulics. When the bottom slope $I$ is increased, they can describe the transition from fluvial to torrential regimes. In the case of an infinitely wide channel, we show that laminar flows have the same critical height $h_{c}$ as that in the turbulent case. This feature is due to the existence of surface slope singularities associated to plug-like velocity profiles with vanishing boundary-layer thickness. We also provide the expression of the critical surface slope as a function of the bottom curvature at the critical location. These results validate a similarity model to approximate the asymptotic Navier–Stokes equations for small slopes $I$ with Reynolds number $Re$ such that $Re\,I$ is of order 1.