Experiments were carried out in a turbulent mixing layer designed to match, as closely as possible, the conditions of the temporally evolving direct numerical simulation of Rogers & Moser (Phys. Fluids, vol. 6, 1994, pp. 903–922). Two Reynolds numbers, based on the local momentum thickness in the self-similar region of the mixing layer, were investigated: 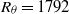 and
and 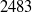 . Measurements were also made in the mixing layer in the pre-mixing transition region where
. Measurements were also made in the mixing layer in the pre-mixing transition region where 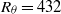 . The three velocity components and their cross-stream gradients were measured with a small 12-sensor hot-wire probe that traversed the mixing layer. Taylor’s hypothesis was used to estimate the streamwise gradients of the velocity components so that reasonably good approximations of all the components of the velocity gradient tensor would be available. The signal from a single-sensor probe at a fixed position in the high-speed free stream flow provided a reference to the phases of the passage of large-scale, coherent, spanwise-oriented vortices past the 12-sensor probe. The velocity and velocity gradient data were analysed to determine turbulence statistical characteristics, including moments, probability density functions and one-dimensional spectra of the velocity and vorticity fields. Although the velocity statistics obtained from the experiment agree well with those from the direct numerical simulation of Rogers & Moser, there are significant differences in the vorticity statistics. The phase reference from the fixed single-sensor probe permitted phase averaging of the 12-sensor probe data so that the spanwise ‘roller’ vortices could be separated from the small-scale, more random turbulence, as had been previously demonstrated by Hussain & Zaman (J. Fluid Mech., vol. 159, 1985, pp. 85–104). In this manner, the data could be conditionally averaged to examine the spatial distributions, with respect to the roller vortices, of interesting and important characteristics of the turbulence, such as the turbulent kinetic energy production and dissipation rate, enstrophy and vorticity component covariances.
. The three velocity components and their cross-stream gradients were measured with a small 12-sensor hot-wire probe that traversed the mixing layer. Taylor’s hypothesis was used to estimate the streamwise gradients of the velocity components so that reasonably good approximations of all the components of the velocity gradient tensor would be available. The signal from a single-sensor probe at a fixed position in the high-speed free stream flow provided a reference to the phases of the passage of large-scale, coherent, spanwise-oriented vortices past the 12-sensor probe. The velocity and velocity gradient data were analysed to determine turbulence statistical characteristics, including moments, probability density functions and one-dimensional spectra of the velocity and vorticity fields. Although the velocity statistics obtained from the experiment agree well with those from the direct numerical simulation of Rogers & Moser, there are significant differences in the vorticity statistics. The phase reference from the fixed single-sensor probe permitted phase averaging of the 12-sensor probe data so that the spanwise ‘roller’ vortices could be separated from the small-scale, more random turbulence, as had been previously demonstrated by Hussain & Zaman (J. Fluid Mech., vol. 159, 1985, pp. 85–104). In this manner, the data could be conditionally averaged to examine the spatial distributions, with respect to the roller vortices, of interesting and important characteristics of the turbulence, such as the turbulent kinetic energy production and dissipation rate, enstrophy and vorticity component covariances.
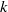 -equation model for large-eddy simulation of compressible flows
-equation model for large-eddy simulation of compressible flows