Article contents
A weakly nonlinear mechanism for mode selection in swirling jets
Published online by Cambridge University Press: 16 April 2012
Abstract
Global linear and nonlinear bifurcation analysis is used to revisit the spiral vortex breakdown of nominally axisymmetric swirling jets. For the parameters considered herein, stability analyses single out two unstable linear modes of azimuthal wavenumber 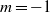 and
and 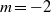 , bifurcating from the axisymmetric breakdown solution. These modes are interpreted in terms of spiral perturbations wrapped around and behind the axisymmetric bubble, rotating in time in the same direction as the swirling flow but winding in space in the opposite direction. Issues are addressed regarding the role of these modes with respect to the existence, mode selection and internal structure of vortex breakdown, as assessed from the three-dimensional direct numerical simulations of Ruith et al. (J. Fluid Mech., vol. 486, 2003, pp. 331–378). The normal form describing the leading-order nonlinear interaction between modes is computed and analysed. It admits two stable solutions corresponding to pure single and double helices. At large swirl, the axisymmetric solution bifurcates to the double helix which remains the only stable solution. At low and moderate swirl, it bifurcates first to the single helix, and subsequently to the double helix through a series of subcritical bifurcations yielding hysteresis over a finite range of Reynolds numbers, the estimated bifurcation threshold being in good agreement with that observed in the direct numerical simulations. Evidence is provided that this selection is not to be ascribed to classical mean flow corrections induced by the existence of the unstable modes, but to a non-trivial competition between harmonics. Because the frequencies of the leading modes approach a strong
, bifurcating from the axisymmetric breakdown solution. These modes are interpreted in terms of spiral perturbations wrapped around and behind the axisymmetric bubble, rotating in time in the same direction as the swirling flow but winding in space in the opposite direction. Issues are addressed regarding the role of these modes with respect to the existence, mode selection and internal structure of vortex breakdown, as assessed from the three-dimensional direct numerical simulations of Ruith et al. (J. Fluid Mech., vol. 486, 2003, pp. 331–378). The normal form describing the leading-order nonlinear interaction between modes is computed and analysed. It admits two stable solutions corresponding to pure single and double helices. At large swirl, the axisymmetric solution bifurcates to the double helix which remains the only stable solution. At low and moderate swirl, it bifurcates first to the single helix, and subsequently to the double helix through a series of subcritical bifurcations yielding hysteresis over a finite range of Reynolds numbers, the estimated bifurcation threshold being in good agreement with that observed in the direct numerical simulations. Evidence is provided that this selection is not to be ascribed to classical mean flow corrections induced by the existence of the unstable modes, but to a non-trivial competition between harmonics. Because the frequencies of the leading modes approach a strong 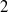 :
: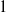 resonance, an alternative normal form allowing interactions between the
resonance, an alternative normal form allowing interactions between the 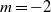 mode and the first harmonics of the
mode and the first harmonics of the 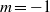 mode is computed and analysed. It admits two stable solutions, the double helix already identified in the non-resonant case, and a single helix differing from that observed in the non-resonant case only by the presence of a slaved, phase-locked harmonic deformation. On behalf of the finite departure from the
mode is computed and analysed. It admits two stable solutions, the double helix already identified in the non-resonant case, and a single helix differing from that observed in the non-resonant case only by the presence of a slaved, phase-locked harmonic deformation. On behalf of the finite departure from the 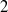 :
: resonance, the amplitude of the slaved harmonic is however low, and the effect of the resonance on the bifurcation structure is merely limited to a reduction of the hysteresis range.
resonance, the amplitude of the slaved harmonic is however low, and the effect of the resonance on the bifurcation structure is merely limited to a reduction of the hysteresis range.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
Meliga et al. supplementary material
Movie 1: animated stable simple helix at Re = 120, S = 1.3. Numerically computed dye lines transported from t=0 up to t = 70 by the second-order analytic solution reconstructed from the asymptotic expansion. The movie has been obtained by initially releasing particles
Meliga et al. supplementary material
Movie 1: animated stable simple helix at Re = 120, S = 1.3. Numerically computed dye lines transported from t=0 up to t = 70 by the second-order analytic solution reconstructed from the asymptotic expansion. The movie has been obtained by initially releasing particles
Meliga et al. supplementary material
Movie 2: same as movie 1 for the stable double helix at Re=150, S=1.3.
Meliga et al. supplementary material
Movie 2: same as movie 1 for the stable double helix at Re=150, S=1.3.
Meliga et al. supplementary material
Movie 3: same as movie 1 for the unstable T2-torus at Re=120, S=1.3.
Meliga et al. supplementary material
Movie 3: same as movie 1 for the unstable T2-torus at Re=120, S=1.3.
- 77
- Cited by


