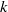 -equation model for large-eddy simulation of compressible flows
-equation model for large-eddy simulation of compressible flowsPublished online by Cambridge University Press: 16 April 2012
This paper presents a dynamic one-equation eddy viscosity model for large-eddy simulation (LES) of compressible flows. The transport equation for subgrid-scale (SGS) kinetic energy is introduced to predict SGS kinetic energy. The exact SGS kinetic energy transport equation for compressible flows is derived formally. Each of the unclosed terms in the SGS kinetic energy equation is modelled separately and dynamically closed, instead of being grouped into production and dissipation terms, as in the Reynolds averaged Navier–Stokes equations. All of the SGS terms in the filtered total energy equation are found to reappear in the SGS kinetic energy equation. Therefore, these terms can be included in the total energy equation without adding extra computational cost. A priori tests using direct numerical simulation (DNS) of decaying isotropic turbulence show that, for a Smagorinsky-type eddy viscosity model, the correlation between the SGS stress and the model is comparable to that from the original model. Also, the suggested model for the pressure dilatation term in the SGS kinetic energy equation is found to have a high correlation with its actual value. In a posteriori tests, the proposed dynamic 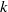 -equation model is applied to decaying isotropic turbulence and normal shock–isotropic turbulence interaction, and yields good agreement with available experimental and DNS data. Compared with the results of the dynamic Smagorinsky model (DSM), the
-equation model is applied to decaying isotropic turbulence and normal shock–isotropic turbulence interaction, and yields good agreement with available experimental and DNS data. Compared with the results of the dynamic Smagorinsky model (DSM), the 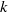 -equation model predicts better energy spectra at high wavenumbers, similar kinetic energy decay and fluctuations of thermodynamic quantities for decaying isotropic turbulence. For shock–turbulence interaction, the
-equation model predicts better energy spectra at high wavenumbers, similar kinetic energy decay and fluctuations of thermodynamic quantities for decaying isotropic turbulence. For shock–turbulence interaction, the 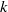 -equation model and the DSM predict similar evolutions of turbulent intensities across shocks, owing to the dominant effect of linear interaction. The proposed
-equation model and the DSM predict similar evolutions of turbulent intensities across shocks, owing to the dominant effect of linear interaction. The proposed 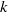 -equation model is more robust in that local averaging over neighbouring control volumes is sufficient to regularize the dynamic procedure. The behaviour of pressure dilatation and dilatational dissipation is discussed through the budgets of the SGS kinetic energy equation, and the importance of the dilatational dissipation term is addressed.
-equation model is more robust in that local averaging over neighbouring control volumes is sufficient to regularize the dynamic procedure. The behaviour of pressure dilatation and dilatational dissipation is discussed through the budgets of the SGS kinetic energy equation, and the importance of the dilatational dissipation term is addressed.