Published online by Cambridge University Press: 24 April 2012
The low-frequency unsteadiness is characterized in the direct numerical simulation of a shock wave–turbulent boundary layer interaction generated by a 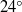 compression ramp in Mach 2.9 flow. Consistent with experimental observations, the shock wave in the simulation undergoes a broadband streamwise oscillation at frequencies approximately two orders of magnitude lower than the characteristic frequency of the energetic turbulent scales in the incoming boundary layer. The statistical relation between the low-frequency shock motion and the upstream and downstream flow is investigated. The shock motion is found to be related to a breathing of the separation bubble and an associated flapping of the separated shear layer. A much weaker statistical relation is found with the incoming boundary layer. In order to further characterize the low-frequency mode in the downstream separated flow, the temporal evolution of the low-pass filtered flow field is investigated. The nature of the velocity and vorticity profiles in the initial part of the interaction is found to change considerably depending on the phase of the low-frequency motion. It is conjectured that these changes are due to an inherent instability in the downstream separated flow, and that this instability is the physical origin of the low-frequency unsteadiness. The low-frequency mode observed here is, in certain aspects, reminiscent of an unstable global mode obtained by linear stability analysis of the mean flow in a reflected shock interaction (Touber & Sandham, Theor. Comput. Fluid Dyn., vol. 23, 2009, pp. 79–107).
compression ramp in Mach 2.9 flow. Consistent with experimental observations, the shock wave in the simulation undergoes a broadband streamwise oscillation at frequencies approximately two orders of magnitude lower than the characteristic frequency of the energetic turbulent scales in the incoming boundary layer. The statistical relation between the low-frequency shock motion and the upstream and downstream flow is investigated. The shock motion is found to be related to a breathing of the separation bubble and an associated flapping of the separated shear layer. A much weaker statistical relation is found with the incoming boundary layer. In order to further characterize the low-frequency mode in the downstream separated flow, the temporal evolution of the low-pass filtered flow field is investigated. The nature of the velocity and vorticity profiles in the initial part of the interaction is found to change considerably depending on the phase of the low-frequency motion. It is conjectured that these changes are due to an inherent instability in the downstream separated flow, and that this instability is the physical origin of the low-frequency unsteadiness. The low-frequency mode observed here is, in certain aspects, reminiscent of an unstable global mode obtained by linear stability analysis of the mean flow in a reflected shock interaction (Touber & Sandham, Theor. Comput. Fluid Dyn., vol. 23, 2009, pp. 79–107).
The movie shows the time-resolved evolution of the low-pass filtered flow field during detailed simulation 1. An isocontour of pressure gradient $|\nabla{p}|\delta/p_{\infty}=2$ indicates the shock, $(u,w)$-streamlines indicate the state of the recirculating flow in the corner, and a color contour map of the spanwise vorticity indicates the structure of the separated shear layer. In addition, the $u$-velocity profile at $x/\delta=-4$ (shown as an inset) indicates the state of the inflow boundary layer. The flow field is spanwise-averaged and low-pass filtered (cutoff Strouhal number 0.22).