Much of our understanding of the transition to turbulence in flows without a linear instability came with the discovery and characterization of fully three-dimensional solutions to the Navier–Stokes equation. The first examples in plane Couette flow were periodic in both spanwise and streamwise directions, and could explain the transitions in small domains only. The presence of localized turbulent spots in larger domains, the spatiotemporal decoherence on larger scales and the ability to trigger turbulence with pointwise perturbations require solutions that are localized in both directions, like the one presented by Brand & Gibson (J. Fluid Mech., vol. 750, 2014, R3). They describe a steady solution of the Navier–Stokes equations and characterize in unprecedented detail, including an analytic computation of its localization properties. The study opens up new ways to describe localized turbulent patches.

We present wall-modelled large-eddy simulations (WLES) of oblique shock waves interacting with the turbulent boundary layers (TBLs) (nominal $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\delta _{99}=5.4\ \mathrm{mm}$ and ${\mathit{Re}}_{\theta }\approx 1.4\times 10^4$) developed inside a duct with an almost-square cross-section ($45\ \mathrm{mm}\times 47.5\ \mathrm{mm}$) to investigate three-dimensional effects imposed by the lateral confinement of the flow. Three increasing strengths of the incident shock are considered, for a constant Mach number of the incoming air stream $M\approx 2$, by varying the height (1.1, 3 and 5 mm) of a compression wedge located at a constant streamwise location that spans the top wall of the duct at a 20° angle. Simulation results are first validated with particle image velocimetry (PIV) experimental data obtained at several vertical planes (one near the centre of the duct and three near one of the sidewalls) for the 1.1 and 3 mm-high wedge cases. The instantaneous and time-averaged structure of the flow for the stronger-interaction case (5 mm-high wedge), which shows mean flow reversal, is then investigated. Additional spanwise-periodic simulations are performed to elucidate the influence of the sidewalls, and it is found that the structure and location of the shock system, as well as the size of the separation bubble, are significantly modified by the lateral confinement. A Mach stem at the first reflected interaction is present in the simulation with sidewalls, whereas a regular shock intersection results for the spanwise-periodic case. Low-frequency unsteadiness is observed in all interactions, being stronger for the secondary shock reflections of the shock train developed inside the duct. The downstream evolution of secondary turbulent flows developed near the corners of the duct as they traverse the shock system is also studied.

The generation, redistribution and, importantly, conservation of vorticity and circulation is studied for incompressible Newtonian fluids in planar and axisymmetric geometries. A generalised formulation of the vorticity at the interface between two fluids for both no-slip and stress-free conditions is presented. Illustrative examples are provided for planar Couette flow, Poiseuille flow, the spin-up of a circular cylinder, and a cylinder below a free surface. For the last example, it is shown that, although large imbalances between positive and negative vorticity appear in the wake, the balance is found in the vortex sheet representing the stress-free surface.

Conditions are found in which stationary turbulent hydraulic jumps can occur in a shallow stably stratified shear flow of depth 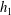$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}h_{1}$ moving over a rigid horizontal boundary at 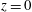$z =0$ and below a deep static layer of uniform density. The flow approaching a jump has uniform density and speed to a height 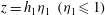$z = h_{1}\eta _{1}\ (\eta _{1} \le 1)$. Above this, in an interfacial layer 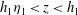$h_{1}\eta _{1}<z<h_{1}$, the density and speed decrease linearly to their values in a deep uniform and static layer above 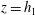$z = h_{1}$. The flow downstream of a jump is supposed to be similarly stratified to a height 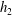$ h_{2}$, but with a lower layer of height 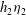$h_{2}\eta _{2}$. The flow approaching the jump is specified by 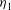$\eta _{1}$ and by a Froude number, Fr. Stationary jumps occur in the flow only if Fr is large enough to ensure that no internal waves can propagate upstream from the transition region. The flow downstream of the jump satisfies conditions of conservation of mass, volume and momentum fluxes, and closure is obtained by the selection of its gradient Richardson number, 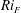${\mathit{Ri}}_{F}$. It is necessary that 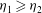$\eta _{1} \ge \eta _{2}$ for the entrainment of fluid into the moving layer from the overlying deep layer to be non-negative. The jump height, 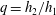$q = h_{2}/h_{1}$, always exceeds unity (i.e. jumps are, overall, of elevation) and the mean thickness of the flowing layer, 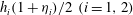$h_{i}(1+ \eta _{i})/2\ (i = 1, 2)$, increases through the jump. There are two types of jumps, one in which the thickness of the lower layer, $h_{i}\eta _{i}$, increases (and all isopycnals are raised by the transition) and a second in which 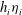$h_{i}\eta _{i}$ decreases even though 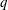$q$ and the mean thickness ratio, 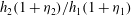$h_{2}(1+ \eta _{2})/ h_{1}(1 + \eta _{1})$, are greater than one. Two possible solutions for the downstream flow (i.e. 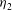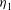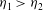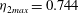two jumps of different heights, $q$, and different shape parameters, $\eta _{2}$) are possible in limited ranges of Fr depending on $\eta _{1}$ when $\eta _{1} > \eta _{2}$, $= \eta _{2max}$, where $\eta _{2max} =0.744$ when 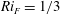${\mathit{Ri}}_{F} = 1/3$. Only single solutions are possible for upstream flows with 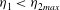$\eta _{1}< \eta _{2max}$. The two branches of the double solutions are distinguishable. For the ‘upper’ solutions, 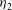$\eta _{2}$ increases as Fr increases, and all isopycnals are raised in the jump. The ‘lower’ of the double solutions are continuous with the single solutions (with 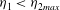$\eta _{1}<\eta _{2max}$), 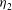$\eta _{2}$ decreases as Fr increases, and for most of the jumps the lower uniform layer decreases in thickness through the jump. For all solutions there is a reduction in the energy flux as fluid passes through a transition, and hence a loss of energy in the turbulent mixing of a jump, as required on physical grounds. The Osborn efficiency factor, 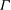$\varGamma $, is generally less than the canonical value of 0.2 for upper branch solutions but greater than 0.2 for the single and lower branch solutions. A loss in vorticity flux occurs in a turbulent jump. For a hydraulic jump to be possible when 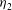$\eta _{2}$ is less than approximately 0.3, it is not generally necessary that the flow approaching a jump is unstable to Kelvin–Helmholtz (K–H) instability, but it is more common that upstream flows in which jumps can occur are dynamically unstable.

This paper is concerned with a particular source of both broadband and tonal aeroengine noise, termed unsteady distortion noise. This noise arises from the interaction between turbulent eddies, which occur naturally in the atmosphere or are shed from the fuselage, and the rotor. This interaction produces broadband noise across a broad frequency spectrum. In cases in which there is strong streamtube contraction, which is especially true for open rotors at low-speed conditions (such as at take-off or for static testing), tonal noise at frequencies equal to multiples of the blade passing frequency are also produced, owing to the enhanced axial coherence caused by eddy stretching. In a previous paper (Majumdar & Peake, J. Fluid Mech., vol. 359, 1998, pp. 181–216), a model for unsteady distortion noise was developed in axisymmetric flow. However, asymmetric situations are also of much interest, and in this paper we consider two cases of asymmetric distortion: firstly that induced by the proximity of a second rotor, and secondly that caused by non-zero inclination to the flight direction, as found at take-off. This requires significant extension of the previous axisymmetric analysis. We find that the introduction of asymmetric flow features can have a significant decibel effect on the radiated sound power. For instance, in low-speed conditions we find that the tonal level is reduced significantly by the proximity of a second rotor, compared to the axisymmetric case, while the effect on the broadband levels is rather modest.

To contribute to the understanding of flow phenomena in abdominal aortic aneurysms, numerical computations of pulsatile flows through aneurysm models and a stability analysis of these flows were carried out. The volume flow rate waveforms into the aneurysms were based on measurements of these waveforms, under rest and exercise conditions, of patients suffering abdominal aortic aneurysms. The Reynolds number and Womersley number, the dimensionless quantities that characterize the flow, were varied within the physiologically relevant range, and the two geometric quantities that characterize the model aneurysm were varied to assess the influence of the length and maximal diameter of an aneurysm on the details of the flow. The computed flow phenomena and the induced wall shear stress distributions agree well with what was found in PIV measurements by Salsac et al. (J. Fluid Mech., vol. 560, 2006, pp. 19–51). The results suggest that long aneurysms are less pathological than short ones, and that patients with an abdominal aortic aneurysm are better to avoid physical exercise. The pulsatile flows were found to be unstable to three-dimensional disturbances if the aneurysm was sufficiently localized or had a sufficiently large maximal diameter, even for flow conditions during rest. The abdominal aortic aneurysm can be viewed as acting like a ‘wavemaker’ that induces disturbed flow conditions in healthy segments of the arterial system far downstream of the aneurysm; this may be related to the fact that one-fifth of the larger abdominal aortic aneurysms are found to extend into the common iliac arteries. Finally, we report a remarkable sensitivity of the wall shear stress distribution and the growth rate of three-dimensional disturbances to small details of the aneurysm geometry near the proximal end. These findings suggest that a sensitivity analysis is appropriate when a patient-specific computational study is carried out to obtain a quantitative description of the wall shear stress distribution.

The stability of premixed flames in a duct is investigated using an asymptotic formulation, which is derived from first principles and based on high-activation-energy and low-Mach-number assumptions (Wu et al., J. Fluid Mech., vol. 497, 2003, pp. 23–53). The present approach takes into account the dynamic coupling between the flame and its spontaneous acoustic field, as well as the interactions between the hydrodynamic field and the flame. The focus is on the fundamental mechanisms of combustion instability. To this end, a linear stability analysis of some steady curved flames is undertaken. These steady flames are known to be stable when the spontaneous acoustic perturbations are ignored. However, we demonstrate that they are actually unstable when the latter effect is included. In order to corroborate this result, and also to provide a relatively simple model guiding active control, we derived an extended Michelson–Sivashinsky equation, which governs the linear and weakly nonlinear evolution of a perturbed flame under the influence of its spontaneous sound. Numerical solutions to the initial-value problem confirm the linear instability result, and show how the flame evolves nonlinearly with time. They also indicate that in certain parameter regimes the spontaneous sound can induce a strong secondary subharmonic parametric instability. This behaviour is explained and justified mathematically by resorting to Floquet theory. Finally we compare our theoretical results with experimental observations, showing that our model captures some of the observed behaviour of propagating flames.

Viscous flows in contact with elastic structures apply both pressure and shear stress at the solid–liquid interface and thus create internal stress and deformation fields within the solid structure. We study the interaction between the deformation of elastic structures, subject to external forces, and an internal viscous liquid. We neglect inertia in the liquid and solid and focus on viscous flow through a thin-walled slender elastic cylindrical shell as a basic model of a soft robot. Our analysis yields an inhomogeneous linear diffusion equation governing the coupled viscous–elastic system. Solutions for the flow and deformation fields are obtained in closed analytical form. The functionality of the viscous–elastic diffusion process is explored within the context of soft-robotic applications, through analysis of selected solutions to the governing equation. Shell material compressibility is shown to have a unique effect in inducing different flow and deformation regimes. This research may prove valuable to applications such as micro-swimmers, micro-autonomous systems and soft robotics by allowing for the design and control of complex time-varying deformation fields.

Roughness-induced transition is one of the main parameters contributing to performance loss of airfoils. Within this paper, the disturbance evolution downstream of a single, cylindrical roughness element, which is placed in a laminar boundary layer in an airfoil leading edge region, is investigated. The experiments focus on medium height roughness elements with respect to the local boundary layer displacement thickness. Hence, transition is not directly tripped at the roughness element. The roughness diameter is comparable to the streamwise wavelength of the most amplified (linear) disturbance eigenmodes. The vortical structures observed downstream of the roughness are in agreement with previous findings in the literature. In the near roughness wake, a distinct growth of high-frequency (fundamental) modes, that is modes with a high $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}n$-factor at the roughness location, is observed. In the far roughness wake, these fundamental modes recover linear stability characteristics due to a possible relaxation of the mean flow. However, an interaction of particularly two-dimensional fundamental modes and by the roughness interference excited oblique fundamental modes results in an excitation of subharmonic type, low-frequency combination modes, which are associated with a phase-locked interaction mechanism. Depending on the initial growth of the fundamental modes in the near wake, the low-frequency modes can experience a nonlinear growth in the far roughness wake and, thereby, trip turbulence. The fundamental mode growth rate in the near wake in turn is a weak function of the disturbance frequency and of the pressure gradient, whereas it is decisively increasing with the roughness height, that is with the mean flow distortion caused by the roughness.

A finite-volume model of the classic differentially heated rotating annulus experiment is used to study the spontaneous emission of gravity waves (GWs) from jet stream imbalances, which may be an important source of these waves in the atmosphere and for which no satisfactory parameterisation exists. Experiments were performed using a classic laboratory configuration as well as using a much wider and shallower annulus with a much larger temperature difference between the inner and outer cylinder walls. The latter configuration is more atmosphere-like, in particular since the Brunt–Väisälä frequency is larger than the inertial frequency, resulting in more realistic GW dispersion properties. In both experiments, the model is initialised with a baroclinically unstable axisymmetric state established using a two-dimensional version of the code, and a low-azimuthal-mode baroclinic wave featuring a meandering jet is allowed to develop. Possible regions of GW activity are identified by the horizontal velocity divergence and a modal decomposition of the small-scale structures of the flow. Results indicate GW activity in both annulus configurations close to the inner cylinder wall and within the baroclinic wave. The former is attributable to boundary layer instabilities, while the latter possibly originates in part from spontaneous GW emission from the baroclinic wave.

We report the existence of interfacial instability in the two-dimensional channel flow of a sediment suspension whose particles diffuse in the carrier fluid due to shear-induced collisions. We derive partial differential equations that govern the deformations of the interface between the sediment suspension and the clear fluid, and devise a perturbation method that preserves the positivity of the particle volume fraction. We solve perturbed momentum, particle transport and deforming interface equations to show that a Kelvin–Helmholtz-type unstable wave develops at the interface for wavelengths longer than a critical value. Short-wavelength oscillations of the interface are damped due to shear-induced diffusion of particles. We also show that the lowest critical Reynolds number, above which the interface is unstable, occurs for intermediate values of the total volume fraction of particles.

We investigate the behaviour of the canonical turbulent Couette flow at computationally high Reynolds number through a series of large-scale direct numerical simulations. We achieve a Reynolds number $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}_{\tau } = h/\delta _v \approx 1000$, where $h$ is the channel half-height and $\delta _v$ is the viscous length scale at which some phenomena representative of the asymptotic Reynolds-number regime manifest themselves. While a logarithmic mean velocity profile is found to provide a reasonable fit of the data, including the skin friction, closer scrutiny shows that deviations from the log law are systematic, and probably increasing at higher Reynolds numbers. The Reynolds stress distribution shows the formation of a secondary outer peak in the streamwise velocity variance, which is associated with significant excess of turbulent production as compared to the local dissipation. This excess is related to the formation of large-scale streaks and rollers, which are responsible for a substantial fraction of the turbulent shear stress in the channel core, and for significant increase of the turbulence intermittency in the near-wall region.

We compute fully local boundary layer scales in three-dimensional turbulent Rayleigh–Bénard convection. These scales are directly connected to the highly intermittent fluctuations of the fluxes of momentum and heat at the isothermal top and bottom walls and are statistically distributed around the corresponding mean thickness scales. The local boundary layer scales also reflect the strong spatial inhomogeneities of both boundary layers due to the large-scale, but complex and intermittent, circulation that builds up in closed convection cells. Similar to turbulent boundary layers, we define inner scales based on local shear stress that can be consistently extended to the classical viscous scales in bulk turbulence, e.g. the Kolmogorov scale, and outer scales based on slopes at the wall. We discuss the consequences of our generalization, in particular the scaling of our inner and outer boundary layer thicknesses and the resulting shear Reynolds number with respect to the Rayleigh number. The mean outer thickness scale for the temperature field is close to the standard definition of a thermal boundary layer thickness. In the case of the velocity field, under certain conditions the outer scale follows a scaling similar to that of the Prandtl–Blasius type definition with respect to the Rayleigh number, but differs quantitatively. The friction coefficient $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}c_{\epsilon }$ scaling is found to fall right between the laminar and turbulent limits, which indicates that the boundary layer exhibits transitional behaviour. Additionally, we conduct an analysis of the recently suggested dissipation layer thickness scales versus the Rayleigh number and find a transition in the scaling. All our investigations are based on highly accurate spectral element simulations that reproduce gradients and their fluctuations reliably. The study is done for a Prandtl number of $\mathit{Pr}=0.7$ and for Rayleigh numbers that extend over almost five orders of magnitude, $3\times 10^5\le \mathit{Ra} \le 10^{10}$, in cells with an aspect ratio of one. We also performed one study with an aspect ratio equal to three in the case of $\mathit{Ra}=10^8$. For both aspect ratios, we find that the scale distributions depend on the position at the plates where the analysis is conducted.

Most turbulent flows appearing in nature (e.g. geophysical and astrophysical flows) are subjected to strong rotation and stratification. These effects break the symmetries of classical, homogenous isotropic turbulence. In doing so, they introduce a natural decomposition of phase space in terms of wave modes and potential vorticity modes. The appearance of a new time scale, associated with the propagation of waves, hinders the understanding of energy transfers across scales. For instance, it is difficult to predict a priori whether the energy cascades downscale as in homogeneous isotropic turbulence or upscale as expected from balanced dynamics. In this paper, we suggest a theoretical approach based on equilibrium statistical mechanics for the ideal system, inspired by the restricted partition function formalism introduced in metastability studies. We focus on the qualitative features of the inviscid system, taking into account either all the modes or just the slow modes. Specifically, we show that at absolute equilibrium, i.e. when all the modes are considered, no negative temperature states exist, and the isotropic energy spectrum is close to equipartition. By contrast, when the statistics is restricted to the contributions of the slow modes, we find that in the presence of rotation, there exists a regime of negative temperature featuring an infrared divergence in both the isotropic and the axisymmetric average energy spectrum, characteristic of an inverse cascade regime. Such regimes are not allowed for purely stratified flows, even in the restricted ensemble, because the slow manifold then partitions into modes that carry potential vorticity on the one hand, and hydrostatically balanced but vorticity-free modes, the so-called vertical shear horizontal flows, on the other hand, which forbid the appearance of negative temperatures.

Using numerical simulations of rapidly rotating Boussinesq convection in a Cartesian box, we study the formation of long-lived, large-scale, depth-invariant coherent structures. These structures, which consist of concentrated cyclones, grow to the horizontal scale of the box, with velocities significantly larger than the convective motions. We vary the rotation rate, the thermal driving and the aspect ratio in order to determine the domain of existence of these large-scale vortices (LSV). We find that two conditions are required for their formation. First, the Rayleigh number, a measure of the thermal driving, must be several times its value at the linear onset of convection; this corresponds to Reynolds numbers, based on the convective velocity and the box depth, $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\gtrsim }100$. Second, the rotational constraint on the convective structures must be strong. This requires that the local Rossby number, based on the convective velocity and the horizontal convective scale, ${\lesssim }0.15$. Simulations in which certain wavenumbers are artificially suppressed in spectral space suggest that the LSV are produced by the interactions of small-scale, depth-dependent convective motions. The presence of LSV significantly reduces the efficiency of the convective heat transport.

We report on experimental determinations of the temperature field in the interior (bulk) of turbulent Rayleigh–Bénard convection for a cylindrical sample with an aspect ratio (diameter $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}D$ over height $L$) equal to 0.50, in both the classical and the ultimate state. The measurements are for Rayleigh numbers $\mathit{Ra}$ from $6\times 10^{11}$ to $10^{13}$ in the classical and $7\times 10^{14}$ to $1.1\times 10^{15}$ (our maximum accessible $\mathit{Ra}$) in the ultimate state. The Prandtl number was close to 0.8. Although to lowest order the bulk is often assumed to be isothermal in the time average, we found a ‘logarithmic layer’ (as reported briefly by Ahlers et al., Phys. Rev. Lett., vol. 109, 2012, 114501) in which the reduced temperature $\varTheta = [\langle T(z) \rangle - T_m]/\Delta T$ (with $T_m$ the mean temperature, $\Delta T$ the applied temperature difference and $\langle {\cdots } \rangle $ a time average) varies as $A \ln (z/L) + B$ or $A^{\prime } \ln (1-z/L) + B^{\prime }$ with the distance $z$ from the bottom plate of the sample. In the classical state, the amplitudes $-A$ and $A^{\prime }$ are equal within our resolution, while in the ultimate state there is a small difference, with $-A/A^{\prime } \simeq 0.95$. For the classical state, the width of the log layer is approximately $0.1L$, the same near the top and the bottom plate as expected for a system with reflection symmetry about its horizontal midplane. For the ultimate state, the log-layer width is larger, extending through most of the sample, and slightly asymmetric about the midplane. Both amplitudes $A$ and $A^{\prime }$ vary with radial position $r$, and this variation can be described well by $A = A_0 [(R - r)/R]^{-0.65}$, where $R$ is the radius of the sample. In the classical state, these results are in good agreement with direct numerical simulations (DNS) for $\mathit{Ra} = 2\times 10^{12}$; in the ultimate state there are as yet no DNS. The amplitudes $-A$ and $A^{\prime }$ varied as ${\mathit{Ra}}^{-\eta }$, with $\eta \simeq 0.12$ in the classical and $\eta \simeq 0.18$ in the ultimate state. A close analogy between the temperature field in the classical state and the ‘law of the wall’ for the time-averaged downstream velocity in shear flow is discussed. A two-sublayer mean-field model of the temperature profile in the classical state was analysed and yielded a logarithmic $z$ dependence of $\varTheta $. The $\mathit{Ra}$ dependence of the amplitude $A$ given by the model corresponds to an exponent $\eta _{th} = 0.106$, in good agreement with the experiment. In the ultimate state the experimental result $\eta \simeq 0.18$ differs from the prediction $\eta _{th} \simeq 0.043$ by Grossmann & Lohse (Phys. Fluids, vol. 24, 2012, 125103).

While the half-angle which encloses a Kelvin ship wave pattern is commonly accepted to be 19.47°, recent observations and calculations for sufficiently fast-moving ships suggest that the apparent wake angle decreases with ship speed. One explanation for this decrease in angle relies on the assumption that a ship cannot generate wavelengths much greater than its hull length. An alternative interpretation is that the wave pattern that is observed in practice is defined by the location of the highest peaks; for wakes created by sufficiently fast-moving objects, these highest peaks no longer lie on the outermost divergent waves, resulting in a smaller apparent angle. In this paper, we focus on the problems of free-surface flow past a single submerged point source and past a submerged source doublet. In the linear version of these problems, we measure the apparent wake angle formed by the highest peaks, and observe the following three regimes: a small Froude number pattern, in which the divergent waves are not visible; standard wave patterns for which the maximum peaks occur on the outermost divergent waves; and a third regime in which the highest peaks form a V-shape with an angle much less than the Kelvin angle. For nonlinear flows, we demonstrate that nonlinearity has the effect of increasing the apparent wake angle so that some highly nonlinear solutions have apparent wake angles that are greater than Kelvin’s angle. For large Froude numbers, the effect on apparent wake angle can be more dramatic, with the possibility of strong nonlinearity shifting the wave pattern from the third regime to the second. We expect that our nonlinear results will translate to other more complicated flow configurations, such as flow due to a steadily moving closed body such as a submarine.

Measurements of normal stress differences are reported for suspensions of rigid, non-Brownian fibres for concentrations of $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}nL^2d=1.5\text {--}3$ and aspect ratios of $L/d=11\text {--}32$, where $n$ is the number of fibres per unit volume, $L$ is the fibre length and $d$ is the diameter. The first and second normal stress differences are determined experimentally from measuring the deformation in the free surface in a tilted trough and in a Weissenberg rheometer. Simulations are performed as well, and the hydrodynamic and contact contributions to the normal stresses are calculated. The experiments and simulations indicate that the second normal stress difference is negative and that its magnitude increases as the concentration is raised and the aspect ratio is lowered. The first normal stress difference is positive and its magnitude is approximately twice that of the second normal stress difference. Simulation results indicate that, for the concentrations and aspect ratios studied, contact forces between fibres form the dominant contribution to the normal stress differences.

The agitation of the liquid phase has been investigated experimentally in a homogeneous swarm of bubbles rising at high Reynolds number within a thin gap. Owing to the wall friction, the bubble wakes are strongly attenuated. Consequently, liquid fluctuations result from disturbances localized near the bubbles and direct interactions between them. The signature of the average wake rapidly fades and the probability density function of the fluctuations becomes Gaussian as the gas volume fraction $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\alpha $ increases. The energy of the fluctuations scales differently with $\alpha $ depending on the direction, indicating that hydrodynamic interactions are different in the horizontal and vertical directions. The spatial spectrum shows that the length scales of the fluctuations are independent of $\alpha $ and exhibits a $k^{-3}$ subrange, which results from localized random flow disturbances of various sizes. Comparisons with the dynamics of the gas phase show that liquid and bubble agitations are driven by the same mechanism in the vertical direction, whereas they turn out to be almost uncoupled in the horizontal direction. Comparisons with unconfined flows show that the generation of liquid fluctuations is very different. However, the cause of the $k^{-3}$ spectral subrange is the same for confined flows as for the spatial fluctuation of unconfined flows.

We propose a continuum model of two-phase flow in a Hele-Shaw cell. The model describes the multiphase three-dimensional flow in the cell gap using gap-averaged quantities such as fluid saturation and Darcy flux. Viscous and capillary coupling between the fluids in the gap leads to a nonlinear fractional flow function. Capillarity and wetting phenomena are modelled within a phase-field framework, designing a heuristic free energy functional that induces phase segregation at equilibrium. We test the model through the simulation of bubbles and viscously unstable displacements (viscous fingering). We analyse the model’s rich behaviour as a function of capillary number, viscosity contrast and cell geometry. Including the effect of wetting films on the two-phase flow dynamics opens the door to exploring, with a simple two-dimensional model, the impact of wetting and flow rate on the performance of microfluidic devices and geological flows through fractures.