Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T23:02:09.382Z Has data issue: false hasContentIssue false
  • English
  • Français

Confinement effects in shock wave/turbulent boundary layer interactions through wall-modelled large-eddy simulations

Published online by Cambridge University Press:  03 October 2014

Iván Bermejo-Moreno ,
Laura Campo ,
Johan Larsson ,
Julien Bodart ,
David Helmer  and
John K. Eaton
Iván Bermejo-Moreno*
Affiliation:
Center for Turbulence Research, Stanford University Stanford, CA 94305, USA
Laura Campo
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA
Johan Larsson
Affiliation:
Center for Turbulence Research, Stanford University Stanford, CA 94305, USA
Julien Bodart
Affiliation:
Center for Turbulence Research, Stanford University Stanford, CA 94305, USA
David Helmer
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA
John K. Eaton
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present wall-modelled large-eddy simulations (WLES) of oblique shock waves interacting with the turbulent boundary layers (TBLs) (nominal 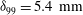$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\delta _{99}=5.4\ \mathrm{mm}$ and 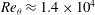${\mathit{Re}}_{\theta }\approx 1.4\times 10^4$) developed inside a duct with an almost-square cross-section (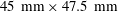$45\ \mathrm{mm}\times 47.5\ \mathrm{mm}$) to investigate three-dimensional effects imposed by the lateral confinement of the flow. Three increasing strengths of the incident shock are considered, for a constant Mach number of the incoming air stream 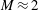$M\approx 2$, by varying the height (1.1, 3 and 5 mm) of a compression wedge located at a constant streamwise location that spans the top wall of the duct at a 20° angle. Simulation results are first validated with particle image velocimetry (PIV) experimental data obtained at several vertical planes (one near the centre of the duct and three near one of the sidewalls) for the 1.1 and 3 mm-high wedge cases. The instantaneous and time-averaged structure of the flow for the stronger-interaction case (5 mm-high wedge), which shows mean flow reversal, is then investigated. Additional spanwise-periodic simulations are performed to elucidate the influence of the sidewalls, and it is found that the structure and location of the shock system, as well as the size of the separation bubble, are significantly modified by the lateral confinement. A Mach stem at the first reflected interaction is present in the simulation with sidewalls, whereas a regular shock intersection results for the spanwise-periodic case. Low-frequency unsteadiness is observed in all interactions, being stronger for the secondary shock reflections of the shock train developed inside the duct. The downstream evolution of secondary turbulent flows developed near the corners of the duct as they traverse the shock system is also studied.

JFM classification

Compressible Flows: Compressible boundary layers Compressible Flows: Shock waves Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , pp. 5 - 62
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Mechanical Engineering, University of Maryland, USA.

§

Present address: Université de Toulouse, ISAE, France.

References

Adamson, T. C. Jr & Messiter, A. F. 1980 Analysis of two-dimensional interactions between shock waves and boundary layers. Annu. Rev. Fluid Mech. 12, 103–138.Google Scholar
Babinsky, H. & Harvey, J. K. 2011 Shock Wave–Boundary-Layer Interactions, Cambridge Aerospace Series. Cambridge University Press.Google Scholar
Balaras, E., Benocci, C. & Piomelli, U. 1996 Two-layer approximate boundary conditions for large-eddy simulations. AIAA J. 34 (6), 111–1119.CrossRefGoogle Scholar
Beresh, S., Clemens, N. & Dolling, D. 2002 Relationship between upstream turbulent boundary-layer velocity fluctuations and separation shock unsteadiness. AIAA J. 40, 2412–2422.CrossRefGoogle Scholar
Bermejo-Moreno, I., Larsson, J. & Lele, S. K. 2010 LES of canonical shock-turbulence interaction. In Annual Research Briefs, pp. 209–222. Center for Turbulence Research.Google Scholar
Bodart, J. & Larsson, J. 2012 Sensor-based computation of transitional flows using wall-modeled large eddy simulation. In Annual Research Briefs, pp. 229–240. Center for Turbulence Research.Google Scholar
Bourgoing, A. & Reijasse, Ph. 2005 Experimental analysis of unsteady separated flows in a supersonic planar nozzle. Shock Waves 14 (4), 251–258.CrossRefGoogle Scholar
Bradshaw, P. 1987 Turbulent secondary flows. Annu. Rev. Fluid Mech. 19, 53–74.Google Scholar
Bruce, P. J. K., Burton, D. M. F., Titchener, N. A. & Babinsky, H. 2011 Corner effect and separation in transonic channel flows. J. Fluid Mech. 679, 247–262.Google Scholar
Cabot, W. 1995 Large-eddy simulations with wall models. In Annual Research Briefs, pp. 41–50. Center for Turbulence Research.Google Scholar
Campo, L. M., Helmer, D. B. & Eaton, J. K.2012 Validation experiment for shock boundary layer interactions: sensitivity to upstream geometric perturbations. AIAA 2012-1440.CrossRefGoogle Scholar
Campo, L. M., Helmer, D. B. & Eaton, J. K.2013 PIV investigation of spanwise variation in incident shock boundary layer interactions. In Proceedings of the 8th TSFP-8. Poitiers, France.Google Scholar
Chapman, D. R. 1979 Computational aerodynamics development and outlook. AIAA J. 17, 1293–1313.CrossRefGoogle Scholar
Chapman, D. R., Kuehn, D. M. & Larson, H. K.1957 Investigations of separated flow in supersonic and subsonic streams with emphasis on the effect of transition. NACA Tech. Rep. R-1356.Google Scholar
Choi, H. & Moin, P. 2012 Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 24, 011702.CrossRefGoogle Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.CrossRefGoogle Scholar
Davis, D. O. & Gessner, F. B. 1989 Further experiments on supersonic turbulent flow development in a square duct. AIAA J. 27 (8), 1023–1030.Google Scholar
Davis, D. O., Gessner, F. B. & Kerlick, G. D. 1986 Experimental and numerical investigation of supersonic turbulent flow through a square duct. AIAA J. 24, 1508–1515.CrossRefGoogle Scholar
Délery, J. & Dussauge, J.-P. 2009 Some physical aspects of shock wave/boundary layer interactions. Shock Waves 19, 453–468.CrossRefGoogle Scholar
Délery, J., Marvin, J. G. & Reshotko, E.1986 Shock-wave boundary layer interactions. Tech. Rep. AGARD-AG-280. NATO, Advisory Group for Aerospace Research and Development.Google Scholar
Dolling, D. S. 2001 Fifty years of shock-wave/boundary-layer interaction research: what next? AIAA J. 39, 1517.Google Scholar
Dolling, D. S. & Or, C. T. 1985 Unsteadiness of the shock wave structure in attached and separated compression ramp flows. Exp. Fluids 3, 24–32.CrossRefGoogle Scholar
Dupont, P., Haddad, C., Ardissone, J. P. & Debiève, J. 2005 Space and time organization of a shock wave/turbulent boundary layer interaction. Aerosp. Sci. Technol. 9, 561–572.Google Scholar
Dupont, P., Haddad, C. & Debiève, J. 2006 Space and time organization in a shock-induced separated boundary layer. J. Fluid Mech. 559, 255–277.CrossRefGoogle Scholar
Dussauge, J.-P., Dupont, P. & Debiève, J.-F. 2006 Unsteadiness in shock wave boundary layer interactions with separation. Aerosp. Sci. Technol. 10 (2), 85–91.CrossRefGoogle Scholar
Edwards, J. R. 2008 Numerical simulations of shock/boundary layer interactions using time-dependent modeling techniques: a survey of recent results. Prog. Aerosp. Sci. 44, 447–465.Google Scholar
Edwards, J. R., Choi, J.-I. & Boles, J. A. 2008 Hybrid large-eddy/Reynolds-averaged Navier–Stokes simulation of a Mach-5 compression corner interaction. AIAA J. 46 (4), 977–991.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2007 Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585, 369–394.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2009 Low-frequency dynamics of shock-induced separation in a compression ramp interaction. J. Fluid Mech. 636, 397–425.Google Scholar
Garg, S. & Settles, G. S. 1996 Unsteady pressure loads generated by swept-shock-wave/boundary-layer interactions. AIAA J. 34 (6), 1174–1181.Google Scholar
Garnier, E. 2009 Stimulated detached eddy simulation of three-dimensional shock/boundary layer interaction. Shock Waves 19, 479–486.Google Scholar
Garnier, E., Sagaut, P. & Deville, M. 2002 Large eddy simulation of shock/boundary-layer interaction. AIAA J. 40 (10), 1935–1944.Google Scholar
Gessner, F. B., Ferguson, S. D. & Lo, C. H. 1987 Experiments on supersonic turbulent flow development in a square duct. AIAA J. 25, 690–697.CrossRefGoogle Scholar
Gibson, B. & Dolling, D. S.1991 Wall pressure fluctuations near separation in a Mach 5, sharp fin-induced turbulent interaction. AIAA Paper 91-0646.Google Scholar
Green, J. E. 1970 Reflexion of an oblique shock wave by a turbulent boundary layer. J. Fluid Mech. 40, 81–95.Google Scholar
Grilli, M., Schmid, P. J., Hickel, S. & Adams, N. A. 2012 Analysis of unsteady behaviour in shockwave turbulent boundary layer interaction. J. Fluid Mech. 700, 16–28.Google Scholar
Gun’ko, Yu. P., Kudryavtsev, A. N. & Rakhimov, R. D. 2004 Supersonic inviscid corner flows with regular and irregular shock interaction. Fluid Dyn. 39 (2), 304–318.Google Scholar
Hadjadj, A., Larsson, J., Morgan, B. E., Nichols, J. W. & Lele, S. K. 2010 Large-eddy simulation of shock/boundary-layer interaction. In Proceedings of the Summer Program, pp. 141–152. Center for Turbulence Research.Google Scholar
Helmer, D., Campo, L. & Eaton, J. 2012 Three-dimensional features of a Mach 2.1 shock/boundary layer interaction. Exp. Fluids 53, 1347–1368.Google Scholar
Helmer, D. & Eaton, J.2011 Measurements of a three-dimensional shock–boundary layer interaction. Tech. Rep. PhD thesis (TF-126). Stanford University.Google Scholar
Hickel, S., Touber, E., Bodart, J. & Larsson, J. 2012 A parametrized non-equilibrium wall-model for large-eddy simulations. In Proceedings of the Summer Program, pp. 127–136. Center for Turbulence Research.Google Scholar
Humble, R., Elsinga, G., Scarano, F. & van Oudheusden, B. 2009a Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction. J. Fluid Mech. 622, 33–62.Google Scholar
Humble, R. A., Scarano, F. & van Oudheusden, B. W. 2009b Unsteady aspects of an incident shock wave/turbulent boundary layer interaction. J. Fluid Mech. 635, 47–74.CrossRefGoogle Scholar
Huser, A. & Biringen, S. 1993 Direct numerical simulation of turbulent flow in a square duct. J. Fluid Mech. 257, 65–95.CrossRefGoogle Scholar
Joung, Y., Choi, S. U. & Choi, J.-I. 2007 Direct numerical simulation of turbulent flow in a square duct: analysis of secondary flows. J. Engng Mech. ASCE 213, 213–221.Google Scholar
Kawai, S. & Larsson, J. 2012 Wall-modeling in large eddy simulation: length scales, grid resolution and accuracy. Phys. Fluids 24, 15105.Google Scholar
Kawai, S. & Larsson, J. 2013 Dynamic non-equilibrium wall-modeling for large eddy simulation at high Reynolds numbers. Phys. Fluids 25, 015105.Google Scholar
Khalighi, Y., Nichols, J. W., Lele, S., Ham, F. & Moin, P.2011 Unstructured large eddy simulations for prediction of noise issued from turbulent jets in various configurations. AIAA 2011-2886.Google Scholar
Klebanoff, P. S.1955 Characteristics of turbulence in a boundary layer with zero pressure gradient. NACA Tech. Rep. 1247.Google Scholar
Klein, M., Sadiki, A. & Janicka, J. 2003 A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 186, 652–665.Google Scholar
Kuehn, D. M.1959 Experimental investigation of the pressure rise required for the incipient separation of turbulent boundary layers in two-dimensional supersonic flow. NASA Memo. 1-21-59A.Google Scholar
Kutler, P. 1974 Supersonic flow in the corner formed by two intersecting wedges. AIAA J. 12 (5), 577–578.Google Scholar
Larsson, J. & Lele, S. K. 2009 Direct numerical simulation of canonical shock/turbulence interaction. Phys. Fluids 21, 126101.CrossRefGoogle Scholar
Lund, T. S., Wu, X. & Squires, K. D. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140, 233–258.Google Scholar
Morgan, B., Duraisamy, K., Nguyen, N., Kawai, S. & Lele, S. K. 2013 Flow physics and RANS modelling of oblique shock/turbulent boundary layer interaction. J. Fluid Mech. 729, 231–284.Google Scholar
Morgan, B., Larsson, J., Kawai, S. & Lele, S. K. 2011 Improving low-frequency characteristics of recycling/rescaling inflow turbulence generation. AIAA J. 49 (3), 582–597.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34, 349–374.Google Scholar
Piponniau, S.2009 Instationnarités dans les décollements compressibles: cas des couches limites soumises à ondes de choc. PhD thesis, L’Univerisité de Provence.Google Scholar
Piponniau, S., Dussauge, J. P., Debiève, J. F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.Google Scholar
Pirozzoli, S. 2012 On the size of the energy-containing eddies in the outer turbulent wall layer. J. Fluid Mech. 702, 521–532.Google Scholar
Pirozzoli, S. & Bernardini, M. 2011 Direct numerical simulation database for impinging shock wave/turbulent boundary-layer interaction. AIAA J. 49 (6), 1307–1312.Google Scholar
Pirozzoli, S. & Grasso, F. 2006 Direct numerical simulation of impinging shock wave/turbulent boundary layer interaction at $M = 2.25$ . J. Comput. Phys. 18 (6), 065113.Google Scholar
Pirozzoli, S., Larsson, J., Nichols, J. W., Bernardini, M., Morgan, B. E. & Lele, S. K. 2010 Analysis of unsteady effects in shock/boundary layer interactions. In Annual Research Briefs, pp. 153–164. Center for Turbulence Research.Google Scholar
Plotkin, K. J. 1975 Shock wave oscillation driven by turbulent boundary-layer fluctuations. AIAA J. 13 (8), 1036–1040.CrossRefGoogle Scholar
Priebe, S. & Martin, M. P. 2012 Low-frequency unsteadiness in shock wave-turbulent boundary layer interaction. J. Fluid Mech. 699, 1–49.Google Scholar
Priebe, S., Wu, M. & Martin, M. P. 2009 Direct numerical simulation of a reflected-shock-wave/turbulent-boundary-layer interaction. AIAA J. 47 (5), 1173–1185.Google Scholar
Ringuette, M. J., Bookey, P., Wyckham, C. & Smits, A. J. 2009 Experimental study of a Mach 3 compression ramp interaction at $\mathit{Re}_{\theta }=2400$ . AIAA J. 47 (2), 373–385.Google Scholar
Souverein, L. J.2010 On the scaling and unsteadiness of shock induced separation. Tech. Rep. PhD thesis, Université de Provence Aix-Marseille I.Google Scholar
Souverein, L., Dupont, P., Debieve, J., van Dussaugen, J., Oudheusden, B. & Scarano, F. 2010 Effect of interaction strength on unsteadiness in turbulent shock-wave-induced separations. AIAA J. 48, 1480–1493.Google Scholar
Spalart, P. R. 2009 Detached-eddy simulation. Annu. Rev. Fluid Mech. 41, 181–202.Google Scholar
Tobak, M. & Peake, D. J. 1982 Topology of three-dimensional separated flows. Annu. Rev. Fluid Mech. 14, 61–85.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Touber, E. & Sandham, N. 2009a Comparison of three large-eddy simulations of shock-induced turbulent separation bubbles. Shock Waves 19 (6), 469–478.Google Scholar
Touber, E. & Sandham, N. 2009b Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23, 79–107.Google Scholar
Touber, E. & Sandham, N. 2011 Low-order stochastic modelling of low-frequency motions in reflected shock-wave/boundary-layer interactions. J. Fluid Mech. 671, 417–465.CrossRefGoogle Scholar
Tutkun, M., George, W. K., Delville, J., Stanislas, M., Johansson, P. B. V., Foucaut, J.-M. & Coudert, S. 2009 Two-point correlations in high Reynolds number flat plate turbulent boundary layers. J. Turbul. 10 (21), 1–23.Google Scholar
Urbin, G. & Knight, D. 2001 Large-eddy simulation of a supersonic boundary layer using an unstructured grid. AIAA J. 39 (7), 1288–1295.Google Scholar
Vreman, A. W. 2004 An eddy-viscosity subgrid-scale model for turbulent shear flow: algebraic theory and applications. Phys. Fluids 16 (10), 3670–3681.Google Scholar
Wang, M. & Moin, P. 2002 Dynamic wall modeling for large-eddy simulation of complex turbulent flows. Phys. Fluids 14 (7), 2043–2051.Google Scholar
Wu, M. & Martin, M. P. 2008 Analysis of shock motion in shockwave and turbulent boundary layer interaction using direct numerical simulation data. J. Fluid Mech. 594, 71–83.Google Scholar
Xie, Z.-T. & Castro, I. P. 2008 Efficient generation of inflow conditions for large eddy simulation of street-scale flows. Flow Turbul. Combust. 81 (3), 449–470.Google Scholar