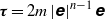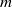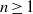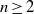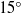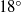Using data from a large-scale three-dimensional simulation of supersonic isothermal turbulence, we have tested the validity of an exact flux relation derived analytically from the Navier–Stokes equation by Falkovich, Fouxon & Oz (J. Fluid Mech., vol. 644, 2010, p. 465). That relation, for compressible barotropic fluids, was derived assuming turbulence generated by a large-scale force. However, compressible turbulence in simulations is usually initialized and maintained by a large-scale acceleration, as in gravity-driven astrophysical flows. We present a new approximate flux relation for isothermal turbulence driven by a large-scale acceleration, and find it in reasonable agreement with the simulation results.

An ensemble average of the equations of motion for a Newtonian fluid over particle configurations in a dilute fixed bed of spheres or cylinders yields Brinkman’s equations of motion, where the disturbance velocity produced by a test particle is influenced by the Newtonian fluid stress and a body force representing the linear drag on the surrounding particles. We consider a similar analysis for a power-law fluid where the stress $\boldsymbol{\tau} $ is related to the rate of strain $ \mathbisf{e} $ by $\boldsymbol{\tau} = 2m \mathop{ \vert \mathbisf{e} \vert }\nolimits ^{n\ensuremath{-} 1} \mathbisf{e} $, where $m$ and $n$ are constants. In this case, the ensemble-averaged momentum equation includes a body force resulting from the nonlinear drag exerted on the surrounding particles, a power-law stress associated with the disturbance velocity of the test particle, and a stress term that is linear with respect to the test particle’s disturbance velocity. The latter term results from the interaction of the test particle’s velocity disturbance with the random straining motions produced by the neighbouring particles and is important only in shear-thickening fluids where the velocity disturbances of the particles are long-ranged. The solutions to these equations using scaling analyses for dilute beds and numerical simulations using the finite element method are presented. We show that the drag force acting on a particle in a fixed bed can be written as a function of a particle-concentration-dependent length scale at which the fluid velocity disturbance produced by a particle is modified by hydrodynamic interactions with its neighbours. This is also true of the drag on a particle in a periodic array where the length scale is the lattice spacing. The effects of particle interactions on the drag in dilute arrays (periodic or random) of cylinders and spheres in shear-thickening fluids is dramatic, where it arrests the algebraic growth of the disturbance velocity with radial position when $n\geq 1$ for cylinders and $n\geq 2$ for spheres. For concentrated random arrays of particles, we adopt an effective medium theory in which the drag force per unit volume in the medium surrounding a test particle is assumed to be proportional to the local volume fraction of the neighbouring particles, which is derived from the hard-particle packing. The predictions of the averaged equations of motion are validated by comparison with simulations of randomly distributed hydrodynamically interacting cylinders.

This study investigates the nonlinear stability of hypersonic viscous flow over a sharp slender cone with passive porous walls. The attached shock and effect of curvature are taken into account. Asymptotic methods are used for large Reynolds number and large Mach number to examine the viscous modes of instability (first Mack mode), which may be described by a triple-deck structure. A weakly nonlinear stability analysis is carried out allowing an equation for the amplitude of disturbances to be derived. The coefficients of the terms in the amplitude equation are evaluated for axisymmetric and non-axisymmetric disturbances. The stabilizing or destabilizing effect of nonlinearity is found to depend on the cone radius. The presence of porous walls significantly influences the effect of nonlinearity, and results for three types of porous wall (regular, random and mesh microstructure) are compared.

In fluid mechanics, multicomponent fluid systems are generally treated either as homogeneous solutions or as completely immiscible parts of a multiphasic system. In immiscible systems, the main task in numerical simulations is to find the location of the interface evolving over time, driven by normal and tangential surface forces. The lattice-Boltzmann method (LBM), on the other hand, is based on a mesoscopic description of the multicomponent fluid systems, and appears to be a promising framework that can lead to realistic predictions of segregation in non-ideal mixtures of partially miscible fluids. In fact, the driving forces in segregation are of a molecular nature: there is competition between the intermolecular forces and the random thermal motion of the molecules. Since these microscopic mechanisms are not accessible from a macroscopic standpoint, the LBM can provide a bridge linking the microscopic and macroscopic domains. To this end, the first purpose of this article is to present the kinetic equations in their continuum forms for the description of the mixing and segregation processes in mixtures. This paper is limited to isothermal segregation; non-isothermal segregation was discussed by Philippi et al. (Phil. Trans. R. Soc., vol. 369, 2011, pp. 2292–2300). Discretization of the kinetic equations leads to evolution equations, written in LBM variables, directly amenable for numerical simulations. Here the dynamics of the kinetic model equations is demonstrated with numerical simulations of a spinodal decomposition problem with dissolution. Finally, some simplified versions of the kinetic equations suitable for immiscible flows are discussed.

Using a simulated highly compressible isotropic turbulence field with turbulent Mach number around 1.0, we studied the effects of local compressibility on the statistical properties and structures of velocity gradients in order to assess salient small-scale features pertaining to highly compressible turbulence against existing theories for incompressible turbulence. A variety of statistics and local flow structures conditioned on the local dilatation – a measure of local flow compressibility – are studied. The overall enstrophy production is found to be enhanced by compression motions and suppressed by expansion motions. It is further revealed that most of the enstrophy production is generated along the directions tangential to the local density isosurface in both compression and expansion regions. The dilatational contribution to enstrophy production is isotropic and dominant in highly compressible regions. The emphasis is then directed to the complicated properties of the enstrophy production by the deviatoric strain rate at various dilatation levels. In the overall flow field, the most probable eigenvalue ratio for the strain rate tensor is found to be −3:1:2.5, quantitatively different from the preferred eigenvalue ratio of −4:1:3 reported in incompressible turbulence. Furthermore, the strain rate eigenvalue ratio tends to be −1:0:0 in high compression regions, implying the dominance of sheet-like structures. The joint probability distribution function of the invariants for the deviatoric velocity gradient tensor is used to characterize local flow structures conditioned on the local dilatation as well as the distribution of enstrophy production within these flow structures. We demonstrate that strong local compression motions enhance the enstrophy production by vortex stretching, while strong local expansion motions suppress enstrophy production by vortex stretching. Despite these complications, most statistical properties associated with the solenoidal component of the velocity field are found to be very similar to those in incompressible turbulence, and are insensitive to the change of local dilatation. Therefore, a good understanding of dynamics of the compressive component of the velocity field is key to an overall accurate description of highly compressible turbulence.

The effect of surface tension on global stability of co-flow jets and wakes at a moderate Reynolds number is studied. The linear temporal two-dimensional global modes are computed without approximations. All but one of the flow cases under study are globally stable without surface tension. It is found that surface tension can cause the flow to be globally unstable if the inlet shear (or, equivalently, the inlet velocity ratio) is strong enough. For even stronger surface tension, the flow is restabilized. As long as there is no change of the most unstable mode, increasing surface tension decreases the oscillation frequency. Short waves appear in the high-shear region close to the nozzle, and their wavelength increases with increasing surface tension. The critical shear (the weakest inlet shear at which a global instability is found) gives rise to antisymmetric disturbances for the wakes and symmetric disturbances for the jets. However, at stronger shear, the opposite symmetry can be the most unstable one, in particular for wakes at high surface tension. The results show strong effects of surface tension that should be possible to reproduce experimentally as well as numerically.

Oblique detonation waves are simulated to study the evolution of their morphology as gasdynamic and chemical parameters are varied. Although two kinds of transition pattern have previously been observed, specifically an abrupt transition and a smooth one, the determining factors for the transition pattern are still unclear. Numerical results show that the transition pattern is influenced by the inflow Mach number, chemical activation energy and heat release. Despite the fact that these parameters were known to influence the detonation instability, the transition pattern variation cannot be predicted according to the instability criterion. In this study, the difference in the oblique shock and detonation angles is proposed as the criterion to determine the transition pattern with the aid of shock-polar analysis. It is found that the smooth transition will appear when the angle difference is small, while the abrupt transition will occur when the difference is large. The shift from the smooth transition to the abrupt transition occurs when the angle difference is about $1{5}^{\ensuremath{\circ} } $–$1{8}^{\ensuremath{\circ} } $. The previously proposed criterion using the characteristic time ratio is also examined and compared with the present angle difference criterion, and the latter is proved to provide better results.