Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T14:40:26.135Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow of power-law fluids in fixed beds of cylinders or spheres

Published online by Cambridge University Press:  29 October 2012

John P. Singh ,
Sourav Padhy ,
Eric S. G. Shaqfeh  and
Donald L. Koch
John P. Singh
Affiliation:
Department of Chemical Engineering and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
Sourav Padhy
Affiliation:
Department of Mechanical Engineering, Stanford University, CA 94305, USA
Eric S. G. Shaqfeh
Affiliation:
Department of Mechanical Engineering, Stanford University, CA 94305, USA Department of Chemical Engineering, Stanford University, CA 94305, USA
Donald L. Koch*
Affiliation:
Department of Chemical Engineering and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An ensemble average of the equations of motion for a Newtonian fluid over particle configurations in a dilute fixed bed of spheres or cylinders yields Brinkman’s equations of motion, where the disturbance velocity produced by a test particle is influenced by the Newtonian fluid stress and a body force representing the linear drag on the surrounding particles. We consider a similar analysis for a power-law fluid where the stress $\boldsymbol{\tau} $ is related to the rate of strain $ \mathbisf{e} $ by 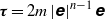$\boldsymbol{\tau} = 2m \mathop{ \vert \mathbisf{e} \vert }\nolimits ^{n\ensuremath{-} 1} \mathbisf{e} $, where 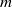$m$ and $n$ are constants. In this case, the ensemble-averaged momentum equation includes a body force resulting from the nonlinear drag exerted on the surrounding particles, a power-law stress associated with the disturbance velocity of the test particle, and a stress term that is linear with respect to the test particle’s disturbance velocity. The latter term results from the interaction of the test particle’s velocity disturbance with the random straining motions produced by the neighbouring particles and is important only in shear-thickening fluids where the velocity disturbances of the particles are long-ranged. The solutions to these equations using scaling analyses for dilute beds and numerical simulations using the finite element method are presented. We show that the drag force acting on a particle in a fixed bed can be written as a function of a particle-concentration-dependent length scale at which the fluid velocity disturbance produced by a particle is modified by hydrodynamic interactions with its neighbours. This is also true of the drag on a particle in a periodic array where the length scale is the lattice spacing. The effects of particle interactions on the drag in dilute arrays (periodic or random) of cylinders and spheres in shear-thickening fluids is dramatic, where it arrests the algebraic growth of the disturbance velocity with radial position when 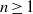$n\geq 1$ for cylinders and 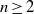$n\geq 2$ for spheres. For concentrated random arrays of particles, we adopt an effective medium theory in which the drag force per unit volume in the medium surrounding a test particle is assumed to be proportional to the local volume fraction of the neighbouring particles, which is derived from the hard-particle packing. The predictions of the averaged equations of motion are validated by comparison with simulations of randomly distributed hydrodynamically interacting cylinders.

JFM classification

Non-Newtonian Flows: Non-Newtonian Flows Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 491 - 527
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baus, M. & Colot, J. L. 1987 Thermodynamics and structure of a fluid of hard rods, disks, spheres, or hyperspheres from rescaled virial expansions. Phys. Rev. A 36 (8), 3912.CrossRefGoogle ScholarPubMed
Brinkman, H. C. 1947 A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A 1 (1), 27.CrossRefGoogle Scholar
Brown, E., Forman, N. A., Orellana, C. S., Zhang, H., Maynor, B. W., Betts, D. E., DeSimone, J. M. & Jaeger, H. M. 2010 Generality of shear thickening in dense suspensions. Nat. Mater. 9 (3), 220–224.CrossRefGoogle ScholarPubMed
Brown, E. & Jaeger, H. M. 2009 Dynamic jamming point for shear thickening suspensions. Phys. Rev. Lett. 103 (8), 86001.CrossRefGoogle ScholarPubMed
Brown, E. & Jaeger, H. M. 2012 The role of dilation and confining stresses in shear thickening of dense suspensions. J. Rheol. 56 (4), 875–923.CrossRefGoogle Scholar
Bruschke, M. V. & Advani, S. G. 1993 Flow of generalized Newtonian fluids across a periodic array of cylinders. J. Rheol. 37, 479.CrossRefGoogle Scholar
Chang, E., Yendler, B. S. & Acrivos, A. 1986 A model for estimating the effective thermal conductivity of a random suspension of spheres. In Advances in Multiphase Flow and Related Problems, Proceedings of the Workshop on Cross Disciplinary Research in Multiphase Flow, Leesburg, VA, 2–4 June 1986 (ed. Papanicolaou, G.). p. 35. Society for Industrial and Applied Mathematics.Google Scholar
Chhabra, R. P., Comiti, J. & Machač, I. 2001 Flow of non-Newtonian fluids in fixed and fluidised beds. Chem. Engng Sci. 56 (1), 1.CrossRefGoogle Scholar
Dazhi, G. & Tanner, R. I. 1985 The drag on a sphere in a power-law fluid. J. Non-Newtonian Fluid Mech. 17 (1), 1.CrossRefGoogle Scholar
Despeyroux, A., Ambari, A. & Richou, A. B. 2011 Wall effects on the transportation of a cylindrical particle in power-law fluids. J. Non-Newtonian Fluid Mech. 166 (19), 1173–1182.CrossRefGoogle Scholar
Duda, J. L., Hong, S. A. & Klaus, E. E. 1983 Flow of polymer solutions in porous media: inadequacy of the capillary model. Ind. Engng Chem. Fundam. 22 (3), 299.CrossRefGoogle Scholar
Ferreira, J. M. & Chhabra, R. P. 2004 Analytical study of drag and mass transfer in creeping power law flow across tube banks. Ind. Engng Chem. Res. 43 (13), 3439–3450.CrossRefGoogle Scholar
Ghannam, M. T. & Esmail, M. N. 1997 Rheological properties of carboxymethyl cellulose. J. Appl. Polym. Sc. 64 (2), 289–301.3.0.CO;2-N>CrossRefGoogle Scholar
Guizar-Sicairos, M. & Gutiérrez-Vega, J. C. 2004 Computation of quasi-discrete Hankel transforms of integer order for propagating optical wave fields. J. Opt. Soc. Am. A 21 (1), 53.CrossRefGoogle ScholarPubMed
Guo, X. & Riebel, U. 2006 Theoretical direct correlation function for two-dimensional fluids of monodisperse hard spheres. J. Chem. Phys. 125, 144504.CrossRefGoogle ScholarPubMed
Happel, J. 1958 Viscous flow in multiparticle systems: slow motion of fluids relative to beds of spherical particles. AIChE J. 4 (2), 197.CrossRefGoogle Scholar
Hill, R. J., Koch, D. L. & Ladd, A. J. C. 2001 The first effects of fluid inertia on flows in ordered and random arrays of spheres. J. Fluid Mech. 448, 213.CrossRefGoogle Scholar
Hinch, E. J. 1977 An averaged-equation approach to particle interactions in a fluid suspension. J. Fluid Mech. 83 (4), 695.CrossRefGoogle Scholar
Howells, I. D. 1974 Drag due to the motion of a Newtonian fluid through a sparse random array of small fixed rigid objects. J. Fluid Mech. 64 (3), 449.CrossRefGoogle Scholar
James, D. F. & McLaren, D. R. 1975 The laminar flow of dilute polymer solutions through porous media. J. Fluid Mech. 70 (4), 733–752.CrossRefGoogle Scholar
Kawase, Y. & Ulbrecht, J. J. 1981 Drag and mass transfer in non-Newtonian flows through multi-particle systems at low Reynolds numbers. Chem. Engng Sci. 36 (7), 1193.CrossRefGoogle Scholar
Kim, S. & Russel, W. B. 1985 Modelling of porous media by renormalization of the Stokes equations. J. Fluid Mech. 154, 269.CrossRefGoogle Scholar
Koch, D. L. & Brady, J. F. 1985 Dispersion in fixed beds. J. Fluid Mech. 154, 399.CrossRefGoogle Scholar
Koch, D. L. & Ladd, A. J. C. 1997 Moderate Reynolds number flows through periodic and random arrays of aligned cylinders. J. Fluid Mech. 349, 31.CrossRefGoogle Scholar
Koch, D. L. & Subramanian, G. 2006 The stress in a dilute suspension of spheres suspended in a second-order fluid subject to a linear velocity field. J. Non-Newtonian Fluid Mech. 138 (2–3), 87.CrossRefGoogle Scholar
Kuwabara, S. 1959 The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers. J. Phys. Soc. Japan 14 (4), 527.CrossRefGoogle Scholar
Marshall, R. J. & Metzner, A. B. 1967 Flow of viscoelastic fluids through porous media. Ind. Engng Chem. Fundam. 6 (3), 393.CrossRefGoogle Scholar
McQuarrie, D. A. 2000 Statistical Mechanics. University Science Books.Google Scholar
Prasad, D. V. N. & Chhabra, R. P. 2001 An experimental investigation of the cross-flow of power law liquids past a bundle of cylinders and in a bed of stacked screens. Can. J. Chem. Engng 79 (1), 28–35.CrossRefGoogle Scholar
Sangani, A. S. & Behl, S. 1989 The planar singular solutions of Stokes and Laplace equations and their application to transport processes near porous surfaces. Phys. Fluids 1, 21.CrossRefGoogle Scholar
Savins, J. G. 1969 Non-Newtonian flow through porous media. Ind. Engng Chem. 61 (10), 18.CrossRefGoogle Scholar
Shaqfeh, E. S. G. & Koch, D. L. 1992 Polymer stretch in dilute fixed beds of fibres or spheres. J. Fluid Mech. 244, 17.CrossRefGoogle Scholar
Sheffield, R. E. & Metzner, A. B. 1976 Flows of nonlinear fluids through porous media. AIChE J. 22 (4), 736.CrossRefGoogle Scholar
Sivakumar, P., Bharti, R. P. & Chhabra, R. P. 2007 Steady flow of power-law fluids across an unconfined elliptical cylinder. Chem. Engng Sci. 62 (6), 1682–1702.CrossRefGoogle Scholar
Spelt, P. D. M., Selerland, T., Lawrence, C. J. & Lee, P. D. 2005 Flows of inelastic non-Newtonian fluids through arrays of aligned cylinders. Part 1. Creeping flows. J. Engng Mech. 51 (1), 57.CrossRefGoogle Scholar
Talwar, K. K. & Khomami, B. 1995 Flow of viscoelastic fluids past periodic square arrays of cylinders: inertial and shear thinning viscosity and elasticity effects. J. Non-Newtonian Fluid Mech. 57 (2), 177–202.CrossRefGoogle Scholar
Tam, C. K. W. 1969 The drag on a cloud of spherical particles in low Reynolds number flow. J. Fluid Mech. 38 (3), 537.CrossRefGoogle Scholar
Tanner, R. I. 1993 Stokes paradox for power-law flow around a cylinder. J. Non-Newtonian Fluid Mech. 50 (2–3), 217.CrossRefGoogle Scholar
Tripathi, A. & Chhabra, R. P. 1992 Slow power law fluid flow relative to an array of infinite cylinders. Ind. Engng Chem. Res. 31 (12), 2754.CrossRefGoogle Scholar
Tsang, L., Kong, J. A., Ding, K. H. & Ao, C. O. 2001 Scattering of Electromagnetic Waves, Numerical Simulations. Wiley-Interscience.CrossRefGoogle Scholar
Vijaysri, M., Chhabra, R. P. & Eswaran, V. 1999 Power-law fluid flow across an array of infinite circular cylinders: a numerical study. J. Non-Newtonian Fluid Mech. 87 (2–3), 263.CrossRefGoogle Scholar
Woods, J. K., Spelt, P. D. M., Lee, P. D., Selerland, T. & Lawrence, C. J. 2003 Creeping flows of power-law fluids through periodic arrays of elliptical cylinders. J. Non-Newtonian Fluid Mech. 111 (2–3), 211.CrossRefGoogle Scholar