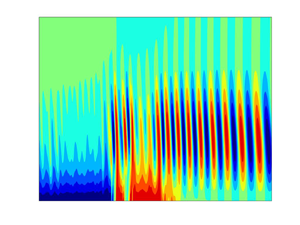
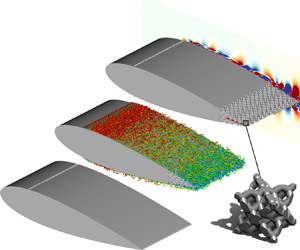
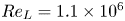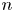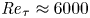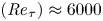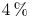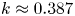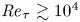Graphical abstract from Habibi, H. & Krechetnikov, R. 2021. Soap film catastrophes. J. Fluid Mech.926, A19. doi:10.1017/jfm.2021.719.
JFM Papers
An adjoint approach for computing the receptivity of the rotating disc boundary layer to surface roughness
-
- Published online by Cambridge University Press:
- 06 September 2021, A16
-
- Article
- Export citation
Numerical analysis of a 3-D printed porous trailing edge for broadband noise reduction
-
- Published online by Cambridge University Press:
- 06 September 2021, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large-eddy simulation and streamline coordinate analysis of flow over an axisymmetric hull
-
- Published online by Cambridge University Press:
- 06 September 2021, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Soap film catastrophes
-
- Published online by Cambridge University Press:
- 06 September 2021, A19
-
- Article
- Export citation
Numerical simulations of the agitation generated by coarse-grained bubbles moving at large Reynolds number
-
- Published online by Cambridge University Press:
- 07 September 2021, A20
-
- Article
- Export citation
Dynamics of a viscoelastic thread surrounded by a Newtonian viscous fluid inside a cylindrical tube
-
- Published online by Cambridge University Press:
- 07 September 2021, A21
-
- Article
- Export citation
A numerical study of a bubble pair rising side by side in external magnetic fields
-
- Published online by Cambridge University Press:
- 07 September 2021, A22
-
- Article
- Export citation
Inertial effects in dusty Rayleigh–Taylor turbulence
-
- Published online by Cambridge University Press:
- 07 September 2021, A23
-
- Article
- Export citation
Parabolic velocity profile causes shape-selective drift of inertial ellipsoids
-
- Published online by Cambridge University Press:
- 07 September 2021, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Developed liquid film passing a smoothed and wedge-shaped trailing edge: small-scale analysis and the ‘teapot effect’ at large Reynolds numbers
-
- Published online by Cambridge University Press:
- 08 September 2021, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Frequency–time analysis, low-rank reconstruction and denoising of turbulent flows using SPOD
-
- Published online by Cambridge University Press:
- 10 September 2021, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motion of a tightly fitting axisymmetric object through a lubricated elastic tube
-
- Published online by Cambridge University Press:
- 10 September 2021, A27
-
- Article
- Export citation
One-point statistics for turbulent pipe flow up to
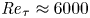 ${\textit {Re}}_{\tau } \approx 6000$
${\textit {Re}}_{\tau } \approx 6000$
-
- Published online by Cambridge University Press:
- 10 September 2021, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mechanisms of dynamic near-wake modulation of a utility-scale wind turbine
-
- Published online by Cambridge University Press:
- 13 September 2021, A29
-
- Article
- Export citation
Turbulence modulation in thermally expanding and contracting flows
-
- Published online by Cambridge University Press:
- 14 September 2021, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reynolds stress scaling in the near-wall region of wall-bounded flows
-
- Published online by Cambridge University Press:
- 14 September 2021, A31
-
- Article
- Export citation
Buoyancy-driven instabilities of partially miscible fluids in inclined porous media
-
- Published online by Cambridge University Press:
- 14 September 2021, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convection in a mushy layer along a vertical heated wall
-
- Published online by Cambridge University Press:
- 14 September 2021, A33
-
- Article
- Export citation
Three-dimensional surface gravity waves of a broad bandwidth on deep water
-
- Published online by Cambridge University Press:
- 15 September 2021, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Charge transport equation for bidisperse collisional granular flows with non-equipartitioned fluctuating kinetic energy
-
- Published online by Cambridge University Press:
- 15 September 2021, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation