Non-wetting substrates allow impacting liquid drops to spread, recoil and take-off, provided they are not too heavy (Biance et al., J. Fluid Mech., vol. 554, 2006, pp. 47–66) or too viscous (Jha et al., Soft Matt., vol. 16, no. 31, 2020, pp. 7270–7273). In this article, using direct numerical simulations with the volume of fluid method, we investigate how viscous stresses and gravity oppose capillarity to inhibit drop rebound. Close to the bouncing to non-bouncing transition, we evidence that the initial spreading stage can be decoupled from the later retraction and take-off, allowing us to understand the rebound as a process converting the surface energy of the spread liquid into kinetic energy. Drawing an analogy with coalescence-induced jumping, we propose a criterion for the transition from the bouncing to the non-bouncing regime, namely by the condition ${Oh}_{c} + {Bo}_{c} \sim 1$, where ${Oh}_{c}$ and ${Bo}_{c}$ are the Ohnesorge number and Bond number at the transition, respectively. This criterion is in excellent agreement with the numerical results. We also elucidate the mechanisms of bouncing inhibition in the heavy and viscous drop limiting regimes by calculating the energy budgets and relating them to the drop's shape and internal flow.

The purpose of the paper is to identify Mach-number effects on pressure fluctuations 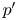$p'$ in compressible turbulent plane channel flow. We use data from a specifically constructed 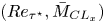$(Re_{\tau ^\star },\bar {M}_{{CL}_x})$-matrix direct numerical simulation (DNS) database, with systematic variation of the centreline streamwise Mach number 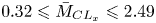$0.32\leqslant \bar {M}_{{CL}_x}\leqslant 2.49$ and of the HCB (Huang et al., J. Fluid Mech., vol. 305, 1995, pp. 185–218) friction Reynolds number 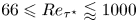$66\leqslant Re_{\tau ^\star }\lessapprox 1000$. Strong 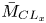$\bar {M}_{{CL}_x}$ effects (enhanced by the increasingly cold-wall condition) appear for 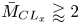$\bar {M}_{{CL}_x}\gtrapprox 2$, for all 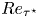$Re_{\tau ^\star }$, very close to the wall (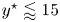$y^\star \lessapprox 15$). Compared with incompressible flow at the same 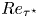$Re_{\tau ^\star }$, the wall root-mean-square 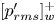$[p'_{rms}]^+_w$ (in wall-units, i.e. scaled by the average wall shear stress 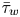$\bar {\tau }_w$) strongly increases with 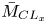$\bar {M}_{{CL}_x}$. In contrast, the peak level across the channel, 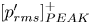$[p'_{rms}]^+_{PEAK}$, slightly decreases with increasing 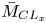$\bar {M}_{{CL}_x}$. In order to study the near-wall coherent structures we introduce a new wall-distance-independent non-local system of units, based for all 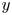$y$ on wall friction and the extreme values of density and dynamic viscosity, namely, for cold walls 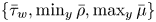$\{\bar {\tau }_w,\min _y\bar {\rho },\max _y\bar {\mu }\}$. The average spanwise distance between streaks, scaled by this length-unit, is nearly independent of 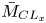$\bar {M}_{{CL}_x}$ at constant 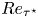$Re_{\tau ^\star }$. Using the in-plane (parallel to the wall) Laplacian 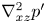$\nabla ^2_{xz}p'$ we find that the 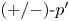$(+/-)\text {-}p'$ wave-packet-like structures appearing inside the low-speed streaks (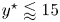$y^\star \lessapprox 15$) with increasing 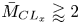$\bar {M}_{{CL}_x}\gtrapprox 2$ are part of a more complex wave system with spanwise extent over several streaks, whose spatial density decreases rapidly with decreasing 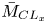$\bar {M}_{{CL}_x}$ or increasing 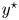$y^\star$. These 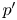$p'$ wave packets appear to be collocated with strong 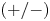$(+/-)$-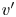$v'$ events and could be responsible for compensating towards 0 the negative incompressible-flow correlation coefficient 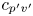$c_{p'v'}$, with increasing 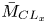$\bar {M}_{{CL}_x}$ very near the wall.

The scattering of three-dimensional inertia-gravity waves by a turbulent geostrophic flow leads to the redistribution of their action through what is approximately a diffusion process in wavevector space. The corresponding diffusivity tensor was obtained by Kafiabad et al. (J. Fluid Mech., vol. 869, 2019, R7) under the assumption of a time-independent geostrophic flow. We relax this assumption to examine how the weak diffusion of wave action across constant-frequency cones that results from the slow time dependence of the geostrophic flow affects the distribution of wave energy. We find that the stationary wave-energy spectrum that arises from a single-frequency wave forcing is localised within a thin boundary layer around the constant-frequency cone, with a thickness controlled by the acceleration spectrum of the geostrophic flow. We obtain an explicit analytic formula for the wave-energy spectrum which shows good agreement with the results of a high-resolution simulation of the Boussinesq equations.

The rebound of droplets impacting a deep fluid bath is studied both experimentally and theoretically. Millimetric drops are generated using a piezoelectric droplet-on-demand generator and normally impact a bath of the same fluid. Measurements of the droplet trajectory and other rebound metrics are compared directly with the predictions of a linear quasipotential model, as well as fully resolved direct numerical simulations of the unsteady Navier–Stokes equations. Both models resolve the time-dependent bath and droplet shapes in addition to the droplet trajectory. In the quasipotential model, the droplet and bath shape are decomposed using orthogonal function decompositions leading to two sets of coupled damped linear harmonic oscillator equations solved using an implicit numerical method. The underdamped dynamics of the drop are directly coupled to the response of the bath through a single-point kinematic match condition which we demonstrate to be an effective and efficient model in our parameter regime of interest. Starting from the inertio-capillary limit in which both gravitational and viscous effects are negligible, increases in gravity or viscosity lead to a decrease in the coefficient of restitution and an increase in the contact time. The inertio-capillary limit defines an upper bound on the possible coefficient of restitution for droplet–bath impact, depending only on the Weber number. The quasipotential model is able to rationalize historical experimental measurements for the coefficient of restitution, first presented by Jayaratne & Mason (Proc. R. Soc. Lond. A, vol. 280, issue 1383, 1964, pp. 545–565).

Analysis of satellite altimetry and Argo float data leads Ni et al. (J. Geophys. Res., 125, 2020, e2020JC016479) to argue that mesoscale dipoles are widespread features of the global ocean having a relatively uniform three-structure that can lead to strong vertical exchanges. Almost all the features of the composite dipole they construct can be derived from a model for multipoles in the surface quasi-geostrophic equations for which we present a straightforward novel solution in terms of an explicit linear algebraic eigenvalue problem, allowing simple evaluation of the higher radial modes that appear to be present in the observations and suggesting that mass conservation may explain the observed frontogenetic velocities.

A general mixed kinetic-diffusion boundary condition is formulated to account for the out-of-equilibrium kinetics in the Knudsen layer. The mixed boundary condition is used to investigate the problem of quasi-steady evaporation of a droplet in an infinite domain containing inert gases. The widely adopted local thermodynamic equilibrium assumption is found to be the limiting case of infinitely large kinetic Péclet number ${{Pe}_k}$, and it introduces significant error for ${{Pe}_k} \leqslant O(10)$, which corresponds to a typical droplet radius $a$ of a few micrometres or smaller. When compared with experimental data, solutions based on the mixed boundary condition, which take into account the temperature jump across the Knudsen layer, better predict the time evolution of $a$ than the classical $D^2$-law (i.e. $a^2 \propto t$, where $t$ denotes time). In the slow evaporation limit, an analytical solution is obtained by linearising the full formulation about the equilibrium condition, which shows that the $D^2$-law can be recovered only in the large ${{Pe}_k}$ limit. For small ${{Pe}_k}$, where the process is dominated by kinetics, a linear relation, i.e. $a \propto t$, emerges. When the gas phase density approaches the liquid density (e.g. at high-pressure or low-temperature conditions), the increase in the chemical potential of the liquid phase due to the presence of inert gases needs to be accounted for when formulating the mixed boundary condition, an effect largely ignored in the literature so far.

Kirby et al. (J. Fluid Mech., vol. 953, 2022, A39) adapted the two-scale momentum theory (Nishino & Dunstan, J. Fluid Mech., vol. 894, A2) to large finite-sized farms. They demonstrated that analytical estimates agree excellently with large eddy simulations, and that the model provides a good upper limit of the power production for a given array density. Crucially, they introduced the concepts of farm-scale losses, caused by the atmospheric response to the whole farm, and turbine-scale losses, owing to internal flow interactions in the wind farm. These two new theoretical concepts offer a novel way to analyse the performance of extended wind farms. For large offshore wind farms, losses at the wind-farm scale are typically twice as high as at the turbine scale. This demonstrates that there is limited potential for layout optimizations of extended arrays. Instead, optimization strategies should focus on developing methods to increase the energy entrainment into the wind farm. This work provides an exciting roadmap for analysing the effective efficiency of large wind farms.

We develop a general framework to describe the cubically nonlinear interaction of a degenerate quartet of deep-water gravity waves in one or two spatial dimensions. Starting from the discretised Zakharov equation, and thus without restriction on spectral bandwidth, we derive a planar Hamiltonian system in terms of the dynamic phase and a modal amplitude. This is characterised by two free parameters: the wave action and the mode separation between the carrier and the sidebands. For unidirectional waves, the mode separation serves as a bifurcation parameter, which allows us to fully classify the dynamics. Centres of our system correspond to non-trivial, steady-state nearly resonant degenerate quartets. The existence of saddle-points is connected to the instability of uniform and bichromatic wave trains, generalising the classical picture of the Benjamin–Feir instability. Moreover, heteroclinic orbits are found to correspond to discrete, three-mode breather solutions, including an analogue of the famed Akhmediev breather solution of the nonlinear Schrödinger equation.

Recent data-driven efforts have utilized spectral decomposition techniques to uncover the geometric self-similarity of dominant motions in the logarithmic layer, and thereby validate the attached eddy model. In this paper, we evaluate the predictive capability of the stochastically forced linearized Navier–Stokes equations in capturing such structural features in turbulent channel flow at $Re_\tau =2003$. We use the linear coherence spectrum to quantify the wall-normal coherence within the velocity field generated by the linearized dynamics. In addition to the linearized Navier–Stokes equations around the turbulent mean velocity profile, we consider an enhanced variant in which molecular viscosity is augmented with turbulent eddy-viscosity. We use judiciously shaped white- and coloured-in-time stochastic forcing to generate a statistical response with energetic attributes that are consistent with the results of direct numerical simulation (DNS). Specifically, white-in-time forcing is scaled to ensure that the two-dimensional energy spectrum is reproduced and coloured-in-time forcing is shaped to match normal and shear stress profiles. We show that the addition of eddy-viscosity significantly strengthens the self-similar attributes of the resulting stochastic velocity field within the logarithmic layer and leads to an inner-scaled coherence spectrum. We use this coherence spectrum to extract the energetic signature of self-similar motions that actively contribute to momentum transfer and are responsible for producing Reynolds shear stress. Our findings support the use of coloured-in-time forcing in conjunction with the dynamic damping afforded by turbulent eddy-viscosity in improving predictions of the scaling trends associated with such active motions in accordance with DNS-based spectral decomposition.

A multiscale asymptotic theory is formulated for surface gravity waves and currents in finite-depth water with a vegetation canopy that provides a drag force on both flows with known drag coefficients. It assumes that the density is uniform and the depth is uniform pro tem and that the wave frequency is fast compared to the current advective rate. It is a quasi-linear theory in which the wave dynamics is independent of current and drag to leading order but provides perturbative corrections, and in which wave nonlinear interactions are neglected while quadratic wave-averaged wave fluxes and quadratic wave-drag effects are retained. The primary surface wave is modified by drag and current interactions, and the wave-averaged current momentum balance includes a wave-augmented drag force and several vortex forces due to Earth's rotation, current vorticity, Stokes drift and drag-induced wave vorticity. The wave-averaged current equations derived here are a suitable basis for future large-eddy simulation and submesoscale circulation computational models.

Numerical simulations for flow past a finite rectangular wing with a NACA 0012 section at $Re=1000$ for various semi-aspect ratios ($0.25\le sAR \le 7.5$) over a range of angles of attack ($0^{\circ }\le \alpha \le 14^{\circ }$) reveal streamwise vortices, which increase in strength and number to occupy an increasing spanwise extent with increase in $\alpha$. They result in non-monotonic spanwise variation of local force coefficients and increased strength of wing-tip vortex for $\alpha >8^{\circ }$. Viscous and pressure drag dominate for low and high sAR, respectively. The time-averaged drag coefficient first decreases and then increases with increase in $sAR$. Vortex shedding for $\alpha =14^{\circ }$ is single cell and parallel for $sAR<3$. Shedding is in two cells with an oblique angle that varies with time, leading to large spanwise variation in the root mean square of local force coefficients for higher $sAR$. Various types of dislocations, reported earlier in wakes of bluff bodies, are seen for different $\alpha$ and $sAR$. Dislocations for $\alpha =14^{\circ }$ appear at the same spanwise location for $sAR=3$ and at different spanwise locations for $sAR\ge 4$. Vortex shedding for $\alpha =12^{\circ }$ and $sAR=5$ exhibits one cell structure in the near wake and two cells in the far wake due to splitting and reconnection of vortices near the mid-span in the moderate wake. Linkages form between counter-rotating spanwise vortices for $sAR\ge 1$. Additional linkages between shed- and wing-tip vortices are observed for lower $sAR$. At each $\alpha$, the strength of the wing-tip vortex and radius of its core, estimated using Rankine and Lamb–Oseen models, increases up to a certain $sAR$ beyond which it is approximately constant.

We introduce maps of Cauchy–Green strain tensor eigenvalues to barycentric coordinates to quantify and visualize the full geometry of three-dimensional deformation in stationary and non-stationary fluid flows. As a natural extension of Lagrangian coherent structure diagnostics, which provide separate scalar fields and a one-dimensional quantification of fluid deformation, our barycentric mapping visualizes the role of all three Cauchy–Green eigenvalues (or rates of stretching) in a single plot through a novel stretching coordinate system. The coordinate system is based on the distance from three distinct limiting states of deformation that correspond with the dimension of the underlying invariant manifolds. One-dimensional axisymmetric deformation (sphere to rod deformation) corresponds to one-dimensional unstable manifolds, two-dimensional axisymmetric deformation (sphere to disk deformation) corresponds to two-dimensional unstable manifolds and the rare three-dimensional isometric case (sphere to sphere translation and rotation) corresponds to shear-free elliptic Lagrangian coherent structures (LCSs). We provide methods to visualize the degree to which fluid deformation approximates these limiting states, and tools to quantify differences between flows based on the compositional geometry of invariant manifolds in the flow. We also develop a simple analogue for bilinearly representing and plotting both rates of stretching and rotation as a single vector. As with other LCS techniques, these diagnostics define frame-indifferent material features in the flow. We provide multiple computed examples of LCS and momentum transport barriers, and show advantages over other coherent structure diagnostics.

In this paper, we investigate the flow past a circular cylinder confined in a channel at a blockage ratio of $\beta =0.7$ (the ratio of the cylinder diameter and the channel height) for Reynolds numbers between ${\textit {Re}}=300$ and $3900$ using direct numerical simulation (DNS). We show for varying Reynolds numbers a wide range of wake dynamics occur as the spanwise domain length is changed. At a lower Reynolds number of ${\textit {Re}}=300$, a reverse von Kármán wake alongside either a top- or bottom-biased asymmetry was observed at different spanwise locations. The asymmetry was structurally similar the two-dimensional asymmetry studied by prior investigators, and was found to be a result of the confinement effect. Further, wake-jumping between the two intermittent states was present. For larger Reynolds numbers, ${\textit {Re}}=1000$ and $3900$, these asymmetric structures were found to become dominant. We also examine the dependence of the asymmetries on the spanwise domain. For small spanwise domains the asymmetries were uniformly orientated across the span. In contrast, for sufficiently large spanwise domains, the asymmetry flips its orientation at different spanwise locations. Comparisons of flow statistics demonstrate good agreement between the different spanwise domains, which suggests the same mechanism maintains the asymmetry in both cases. Further analysis at ${\textit {Re}}=1000$ found the number of times the wake flips is dependent on the initial conditions, with a wake that flips zero (purely asymmetric), two and four times being observed. These structures were also determined to remain stable over time scales of $1000D/U$.

We report on the modification of the spectrum of a passive scalar inside a turbulent flow by the injection of large bubbles. Although the spectral modification through bubbles is well known and well analysed for the velocity fluctuations, little is known on how bubbles change the fluctuations of an approximately passive scalar, in our case temperature. Here we uncover the thermal spectral scaling behaviour of a turbulent multiphase thermal mixing layer. The development of a $-3$ spectral scaling is triggered. By injecting large bubbles (${Re}_{{bub}} = {O}(10^2)$) with gas volume fractions $\alpha$ up to 5 %. For these bubbly flows, the $-5/3$ scaling is still observed at intermediate frequencies for low $\alpha$ but becomes less pronounced when $\alpha$ further increases and it is followed by a steeper $-3$ slope for larger frequencies. This $-3$ scaling range extends with increasing gas volume fraction. The $-3$ scaling exponent coincides with the typical energy spectral scaling for the velocity fluctuations in high-Reynolds-number bubbly flows. We identify the frequency scale of the transition from the $-5/3$ scaling to the $-3$ scaling and show how it depends on the gas volume fraction.

Fast microjets can emerge out of liquid pools from the rebounding of drop-impact craters, or when a bubble bursts at its surface. The fastest jets are the narrowest and are a source of aerosols both from the ocean and from a glass of champagne, of importance to climate and the olfactory senses. The most singular jets, which we observe experimentally at a maximum velocity of $137\pm 4\ {\rm m}\ {\rm s}^{-1}$ and a diameter of $12\ \mathrm {\mu }{\rm m}$, under reduced ambient pressure, are produced when a small dimple forms at the crater bottom and rebounds without pinching off a small bubble. The radial collapse and rebounding of this dimple is purely inertial, but highly sensitive to initial conditions. High-resolution numerical simulations reveal a new focusing mechanism, which drives the fastest jet within a converging conical channel, where an entrained air sheet provides effective slip at the outer boundary of the conically converging flow into the jet. This configuration bypasses any viscous cutoff of the jetting speed and explains the extreme sensitivity to initial conditions observed in detailed experiments of the phenomenon.

Tonal noise emitted from the trailing edge of an airfoil is considered using modal analysis techniques to investigate secondary quadrupole tones. We examine the origin of quadrupole sound generated from two-dimensional unsteady laminar flow over a NACA0012 airfoil. In this paper, we consider two flow configurations at Mach numbers of $M_\infty = 0.1$ and 0.05 that lead to different acoustic characteristics: the former has a significant high-frequency quadrupole noise source, whereas the latter does not. We use vortex sound theory, dynamic mode decomposition (DMD), and resolvent analysis to analyze the sound source. First, we employ DMD modes to reveal that the quadrupole sound is only observed in the higher Mach number case. Next, the vortex dynamics in the vicinity of the trailing edge are studied to identify the origin of quadrupole sound. It is found that the quadrupole sound is caused by vortex shedding in the vicinity of the trailing edge. The complex vortex interaction between both sides of the airfoil strengthens the quadrupole source in the higher Mach number case, while it is negligible in the lower one. Furthermore, we perform resolvent analysis to examine the vortex generation over the airfoil. The resolvent mode indicates that the interaction between the vortices on both sides of the airfoil causes a multi-scale vortex structure on the suction-side wall.

The shape of depth-limited breaking-wave overturns is important for turbulence injection, bubble entrainment and sediment suspension. Overturning wave shape depends on a nonlinearity parameter $H/h$, where $H$ is the wave height, and $h$ is the water depth. Cross-shore wind direction (offshore/onshore) and magnitude affect laboratory shoaling wave shape and breakpoint location $X_{{bp}}$, but wind effects on overturning wave shape are largely unstudied. We perform field-scale experiments at the Surf Ranch wave basin with fixed bathymetry and $\approx 2.25$ m shoaling solitons with small height variations propagating at $C=6.7\ \mathrm {m}\ \mathrm {s}^{-1}$. Observed non-dimensional cross-wave wind $U_w$ was onshore and offshore, varying realistically ($-1.2 < U_{w}/C < 0.7$). Georectified images, a wave staff, and lidar are used to estimate $X_{{bp}}$, $H/h$, overturn area $A$ and aspect ratio for 22 waves. The non-dimensionalized $X_{{bp}}$ was inversely related to $U_{w}/C$. The non-dimensional overturn area and aspect ratio also were inversely related to $U_{w}/C$, with smaller and narrower overturns for increasing onshore wind. No overturning shape dependence on the weakly varying $H/h$ was seen. The overturning shape variation was as large as prior laboratory experiments with strong $H/h$ variations without wind. An idealized potential air flow simulation on steep shoaling soliton shape has strong surface pressure variations, potentially inducing overturning shape changes. Through wave-overturning impacts on turbulence and sediment suspension, coastal wind variations could be relevant for near-shore morphology.

Direct numerical simulations (DNS) of a jet in cross-flow (JICF) with a triangular tab at two positions are performed at jet-to-cross-flow velocity ratios of $R = 2$ and $4$ with a jet Reynolds number of 2000 based on the jet's bulk velocity and exit diameter. The DNS and dynamic mode decomposition show the sensitivity of the tab's effect on the jet upstream shear layer (USL) structure and cross-section to $R$, echoing the experimental discoveries of Harris et al. (J. Fluid Mech., vol. 918, 2021). Furthermore, DNS reveals that the presence of a tab placed on the upstream side of the nozzle significantly modifies the USL through production of streamwise vortices that curl around the spanwise vortex tubes originating from the primary instability of the USL. This provides an explanation for the improvement in mixing that has been associated with an upstream tab. The streamwise vortex structure shows remarkable similarities to the ‘strain-oriented vortex tubes’ observed for disturbed plane shear layers by Lasheras & Choi (J. Fluid Mech., vol. 189, 1988, pp. 53–86). For both $R$ cases, the USL instability is delayed, the jet penetration is reduced, and the jet cross-section is flattened, although the tab has a less pronounced effect on the USL structure at higher velocity ratios, where the formation of the streamwise vortices is delayed. In contrast, a tab placed 45$^\circ$ from the upstream position produces significantly different effects compared with the upstream tab. At $R = 4$, the jet cross-section is significantly skewed away from the tab and a tertiary vortex is formed, as observed in past studies of round JICFs at relatively high $R$ and low Reynolds numbers. The ability of the tab to produce a controllable steady-state tertiary vortex has implications for a variety of applications. The 45$^\circ$ tab produces asymmetric effects in the wake of the jet at $R = 2$, but the effect on the jet cross-section is much smaller, highlighting the sensitivity of jets at high $R$ to asymmetric perturbations.

Wall-bounded turbulent flows exhibit a zonal arrangement, in which streamwise velocity organizes into uniform momentum zones (UMZs), separated by thin layers of elevated interfacial shear. While significant research efforts have focused on these structural features in neutrally stratified flows, the effects of unstable thermal stratification on UMZs and on analogous uniform temperature zones (UTZs) have not been considered previously. In this article, statistical properties of UMZs and UTZs are investigated using a suite of large eddy simulations of unstably stratified turbulent channel flow spanning weakly to highly convective conditions. When normalized by the friction velocity and stability-dependent mixing length, the mean velocity gradient based on UMZ interfacial velocity jumps and the vorticity thickness exhibits good collapse for all stabilities, establishing a link between UMZ properties and scaling predictions from Monin–Obukhov similarity theory. A similar relationship is found between UTZ properties and surface-layer scaling of the mean temperature gradient. In the mixed layer, mean UMZ depth is quasi-constant with wall-normal distance, while the deepest UTZs are found in the centre of the boundary layer. These instantaneous structures are found to be linked to the well-mixed velocity and temperature profiles in the convective mixed layer. Conditional averaging indicates that both UMZ and UTZ interfaces are associated with ejections of momentum and warm updrafts below the interface and sweeps of momentum and cool downdrafts above the interface. These results demonstrate a tangible connection between instantaneous structural features, mean properties and scaling laws in unstably stratified flows.

Recent direct numerical simulation studies of canonical shock–isotropic turbulence interactions (SITIs) in the highly compressible regime exhibit streamwise Reynolds stress amplification that is significantly higher in some cases than in previous studies; an explanation is offered based on a relatively high Mach number combined with significant dilatational energy in the incident flow. Some cases exhibit a loss of amplification that is associated with a highly perturbed shock structure as the flow parameters approach the threshold between the wrinkled and broken shock regimes. The shock structure perturbations due to the highly compressible incident turbulence match those proposed by Donzis (Phys. Fluids, vol. 24, 2012, 126101) relatively well, but due to the presence of thermodynamic fluctuations in addition to velocity fluctuations in the incident flow, we propose a generalized parametrization based on the root-mean-square Mach number fluctuation in place of the turbulence Mach number. This is found to improve the collapse of the shock structure data, suggesting that the wrinkled–broken shock regime threshold determined previously for vortical turbulence (Donzis, Phys. Fluids, vol. 24, 2012, 126101; Larsson et al., J. Fluid Mech., vol. 717, 2013, pp. 293–321) can be applied to more general isotropic inflow fields using the proposed parametrization.