Understanding and predicting the dynamics of dispersed micro-objects in microfluidics is crucial in numerous natural, industrial and technological situations. In this paper, we experimentally characterized the equilibrium velocity 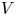 $V$ and lateral position
$V$ and lateral position 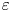 $\varepsilon$ of various dispersed micro-objects, such as beads, bubbles and drops, in a cylindrical microchannel over an unprecedentedly wide range of parameters. By varying the dimensionless object size (
$\varepsilon$ of various dispersed micro-objects, such as beads, bubbles and drops, in a cylindrical microchannel over an unprecedentedly wide range of parameters. By varying the dimensionless object size (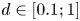 $d \in [0.1; 1]$), the viscosity ratio (
$d \in [0.1; 1]$), the viscosity ratio (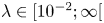 $\lambda \in [10^{-2}; \infty [$), the density ratio (
$\lambda \in [10^{-2}; \infty [$), the density ratio (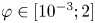 $\varphi \in [10^{-3}; 2]$), the Reynolds number (
$\varphi \in [10^{-3}; 2]$), the Reynolds number (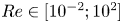 $Re \in [10^{-2}; 10^2]$) and the capillary number (
$Re \in [10^{-2}; 10^2]$) and the capillary number (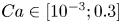 $Ca \in [10^{-3}; 0.3]$), we offer an exhaustive parametric study exploring various dynamics from the non-deformable viscous regime to the deformable inertial regime, thus enabling us to highlight the sole and combined roles of inertia and capillary effects on lateral migration. Experiments are compared and agree well with a steady three-dimensional Navier–Stokes model for incompressible two-phase fluids, including the effects of inertia and possible interfacial deformations. This model enables us to propose a correlation for the object velocity
$Ca \in [10^{-3}; 0.3]$), we offer an exhaustive parametric study exploring various dynamics from the non-deformable viscous regime to the deformable inertial regime, thus enabling us to highlight the sole and combined roles of inertia and capillary effects on lateral migration. Experiments are compared and agree well with a steady three-dimensional Navier–Stokes model for incompressible two-phase fluids, including the effects of inertia and possible interfacial deformations. This model enables us to propose a correlation for the object velocity 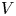 $V$ as functions of
$V$ as functions of 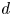 $d$,
$d$, 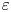 $\varepsilon$ and
$\varepsilon$ and 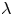 $\lambda$, obtained in the
$\lambda$, obtained in the 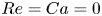 ${Re}={Ca}=0$ limit, but valid for a larger range of values of
${Re}={Ca}=0$ limit, but valid for a larger range of values of 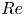 ${Re}$ and
${Re}$ and 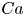 ${Ca}$ delimited by the validity of the linear regime. Next, we present stability maps for the centred position showing that non-deformable objects dominated by inertial effects are only stable if large enough, typically for
${Ca}$ delimited by the validity of the linear regime. Next, we present stability maps for the centred position showing that non-deformable objects dominated by inertial effects are only stable if large enough, typically for 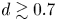 $d \gtrsim 0.7$, whereas deformable objects dominated by capillary effects can be stable for much smaller sizes, provided the viscosity ratio is outside the range
$d \gtrsim 0.7$, whereas deformable objects dominated by capillary effects can be stable for much smaller sizes, provided the viscosity ratio is outside the range 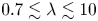 $0.7 \lesssim \lambda \lesssim 10$, in which deformability also plays a destabilizing effect, as for inertia.
$0.7 \lesssim \lambda \lesssim 10$, in which deformability also plays a destabilizing effect, as for inertia.
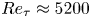 $Re_\tau \approx 5200$
$Re_\tau \approx 5200$