Research Article
Primes with an average sum of digits
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2009, pp. 271-292
-
- Article
-
- You have access
- Export citation
Tate–Shafarevich groups in anticyclotomic ℤp-extensions at supersingular primes
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2009, pp. 293-308
-
- Article
-
- You have access
- Export citation
Brauer–Manin obstruction for integral points of homogeneous spaces and representation by integral quadratic forms
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2009, pp. 309-363
-
- Article
-
- You have access
- Export citation
p-units in ray class fields of real quadratic number fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2009, pp. 364-392
-
- Article
-
- You have access
- Export citation
Singularities on normal varieties
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2009, pp. 393-414
-
- Article
-
- You have access
- Export citation
The affine part of the Picard scheme
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2009, pp. 415-422
-
- Article
-
- You have access
- Export citation
Intersection theory on Shimura surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2009, pp. 423-475
-
- Article
-
- You have access
- Export citation
Quantum subgroups of a simple quantum group at roots of one
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2009, pp. 476-500
-
- Article
-
- You have access
- Export citation
A Plancherel formula for Sp2n/Spn×Spn and its application
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2009, pp. 501-527
-
- Article
-
- You have access
- Export citation
On manifolds with quadratic curvature decay
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2009, pp. 528-540
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
COM volume 145 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 15 April 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
COM volume 145 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 15 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation


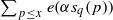 (where the sum is restricted to
(where the sum is restricted to 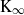 the anticyclotomic ℤ
the anticyclotomic ℤ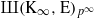 has trivial Λ-corank and, in the process, also show that
has trivial Λ-corank and, in the process, also show that 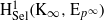 and
and  both have Λ-corank two.
both have Λ-corank two. .
.