We axiomatize the theory of real and complex numbers in Boolean-valued models of set theory, and prove that every Horn sentence true in the complex numbers is true in any complete Stonean algebra, and provable from its axioms.

It is shown that, if F and G are inner functions, (H2 ⊖ FH2)/(H2 ⊖ FH2) ∩ GH2 is n-dimensional if and only if G is a Blaschke product of degree n. This is an extension of the well known result for the case (H2 ⊖ FH2) ∩ GH2 = {0}.

Let x denote a primitive character to a prime-power modulus k = pα. The expected estimate

for the incomplete character sum has been established for r = 1 and 2 by D. A. Burgess and recently, he settled the case r = 3 for all primes p < 3, (cf. [2] for the proof and for references). Here, a short proof of the main inequality (Theorem 2) which leads to this result is presented; the argument being based upon my characterization in [3] of the solution-set of a related congruence.

The Mahler measure M (α) of an algebraic integer α is the product of the moduli of the conjugates of α which lie outside the unit circle. A number α is reciprocal if α- 1 is a conjugate of α. We give two constructions of reciprocal a for which M (α) is non-reciprocal producing examples of any degree n of the form 2h with h odd and h ≥ 3, or else of the form with s ≥ 2. We give explicit examples of degrees 10, 14 and 20.

A theorem concerning M-summands in dual spaces is used to prove that certain known M-ideals are not M-summands. In some cases where this information was already known, our procedure greatly simplifies the earlier proofs. Finally, we give a condition to determine which M-ideals in dual spaces are M-summands and which are not.

Knopp's inequality for convex functions ϕ on an interval I = [m,M] states that

for an explicit functional H, and all integrable g: [0, 1] → I. In this paper we give results of this kind in which the integral operator, ∫, is replaced by a general isotonic linear functional.

Let (αn.k) be a sequence of positive numbers. We define a regular sequence (resp. a weakly regular sequence) and then show the existence of a unitary operator (resp. a contraction T) L2[0, 1] → L2[0, 1] and a function f ∊ L2[0, 1] such that the pointwise convergence of the sequence of functions is not satisfied almost surely. As a first corollary the pointwise convergence of the Abel means of a contraction from L2 into L2 does not hold necessarily almost surely. As a second corollary there exists a contraction T for which the means (and powers) of Brunei's operator A do not converge pointwise a.s. We also show that, for P > 1 fixed, there exists a sequence of positive numbers αn.k for which we have the pointwise convergence in LP of the sequence of polynomials 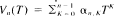where T is a contraction of L1 and Lα. The dominated theorem does not, however, always hold for such LP-contractions.

A theorem of G. Higman about the embeddability of amalgams within the class of all finite ρ-groups is generalized to classes of soluble groups. We also give best possible bounds for the solubility lengths of the constructed completions. And, as an application, the super-soluble amalgamation bases in the class of all finite soluble π-groups are determined.

Dickson polynomials over finite fields are familiar examples of permutation polynomials, i.e. of polynomials for which the corresponding polynomial mapping is a permutation of the finite field. We prove that a Dickson polynomial can be a complete mapping polynomial only in some special cases. Complete mapping polynomials are of interest in combinatorics and are defined as polynomials f(x) over a finite field for which both f(x) and f(x) + x are permutation polynomials. Our result also verifies a special case of a conjecture of Chowla and Zassenhaus on permutation polynomials.

This is a sequel to the author's paper "On the semigroup of probability measures of a locally compact semigroup." We continue to investigate the relationship between amenability of spaces of functions and functionals associated with a locally compact semigroups S and its convolution semigroup MO(S) of probability measures and fixed point properties of actions of S and MO(S) on compact convex sets.

Let R be a 2-torsion free associative ring with involution. It is shown that if the set S of symmetric elements is nilpotent as a Jordan ring then R is nilpotent.

We show that a locally compact semigroup S is topological left amenable iff a certain space of left uniformly continuous functions on the convolution semigroup of probability measures M0(S) on S is left amenable or equivalently iff the convolution semigroup M0(S) has the fixed point property for uniformly continuous affine actions on compact convex sets.

Let G(x,s) be the Green's function for the boundary value problem y(n) = 0, Ty = 0, where Ty = 0 represents boundary conditions at two points. The signs of G(x,s) and certain of its partial derivatives with respect to x are determined for two classes of boundary value problems. The results are also carried over to analogous classes of boundary value problems for difference equations.

Milnor showed that non-singular bilinear products on Rn exist only if n = 1, 2, 4, 8 using topological methods. In this note, we give a proof of this result by purely analytical methods.

The construction, from a consistent family of finite dimensional probability measures, of a probability measure on a product space when the marginal measures are perfect is shown to follow from a classical theorem due to Ionescu Tulcea and known results on the existence of regular conditional probability functions.

The concept of H-semidirect product structure on a grouplike space is introduced. It is shown that the loop space ΩX of any based CW-complex X is the H-semidirect product of the identity path-component of ΩX with π1,X. The set of free homotopy classes of maps into a Hsemidirect product inherits the structure of a semidirect product. This leads to new results concerning the nilpotency of homotopy classes of maps into a group-like space.

If A is an elementary abelian ρ-group and C one of its cyclic subgroups, the integral group rings ZA contains, of course, the ring ZC. It will be shown below, for A of rank 2 and ρ a regular prime, that every unit of ZA is a product of units of ZC, as C ranges over all cyclic subgroups.

The paper describes polyhedral realizations for Felix Klein's map {3, 7}8 of genus 3, for Gordan's map {4, 5}6 of genus 4, and for two maps of genus 5, the Klein-Fricke map of type {3, 8} and Sherk's map of type {4, 6}. The polyhedra have self-intersections but high symmetry and thus are close analogues to the Kepler-Poinsot-polyhedra.

Let G(n) denote the number of non-isomorphic groups of order n. We prove that for squarefree integers n, there is a constant A such that

where denotes the Euler function. This upper bound is essentially best possible, apart from the constant A.

We determine, except for one unsettled case, which combinations of Weierstrass weights can occur on irreducible rational nodal curves of arithmetic genus three. It is shown that the number of nonsingular Weierstrass points on such curves can be any integer between 0 and 6, except 1.