The norm on a Banach space gives rise to a subharmonic function on the complex plane for which the distributional Laplacian gives a Riesz measure. This measure is calculated explicitly here for Lebesgue ${{L}^{p}}$ spaces and the von Neumann-Schatten trace ideals. Banach spaces that are $q$-uniformly $\text{PL}$-convex in the sense of Davis, Garling and Tomczak-Jaegermann are characterized in terms of the mass distribution of this measure. This gives a new proof that the trace ideals ${{c}^{p}}$ are 2-uniformly $\text{PL}$-convex for $1\,\le \,p\,\le \,2$.

Nous étudions la structure du centralisateur d'un élément unipotent régulier d'un sous-groupe de Levi d'un groupe réductif, ainsi que la structure du groupe des composantes de ce centralisateur en relation avec la notion de système local cuspidal définie par Lusztig. Nous déterminons son radical unipotent, montrons l'existence d'un complément de Levi et étudions la structure de son groupe de Weyl. Comme application, nous démontrons des résultats qui étaient annoncés dans un précédent article de l'auteur sur les éléments unipotents réguliers.

It is shown that the singular values of the operator $aP\,-\,Pa$, where $P$ is Bergman's projection over a bounded domain $\Omega $ and $a$ is a function analytic on $\bar{\Omega }$, detect the length of the boundary of $a\left( \Omega \right)$. Also we point out the relation of that operator and the spectral asymptotics of a Hankel operator with an anti-analytic symbol.

We study the structure of generalized Verma modules over a semi-simple complex finite-dimensional Lie algebra, which are induced from simple modules over a parabolic subalgebra. We consider the case when the annihilator of the starting simple module is a minimal primitive ideal if we restrict this module to the Levi factor of the parabolic subalgebra. We show that these modules correspond to proper standard modules in some parabolic generalization of the Bernstein-Gelfand-Gelfand category $\mathcal{O}$ and prove that the blocks of this parabolic category are equivalent to certain blocks of the category of Harish-Chandra bimodules. From this we derive, in particular, an irreducibility criterion for generalized Verma modules. We also compute the composition multiplicities of those simple subquotients, which correspond to the induction from simple modules whose annihilators are minimal primitive ideals.

In this article we determine the global geometry of the planar quadratic differential systems with a weak focus of third order. This class plays a significant role in the context of Hilbert's 16-th problem. Indeed, all examples of quadratic differential systems with at least four limit cycles, were obtained by perturbing a system in this family. We use the algebro-geometric concepts of divisor and zero-cycle to encode global properties of the systems and to give structure to this class. We give a theorem of topological classification of such systems in terms of integer-valued affine invariants. According to the possible values taken by them in this family we obtain a total of 18 topologically distinct phase portraits. We show that inside the class of all quadratic systems with the topology of the coefficients, there exists a neighborhood of the family of quadratic systems with a weak focus of third order and which may have graphics but no polycycle in the sense of [15] and no limit cycle, such that any quadratic system in this neighborhood has at most four limit cycles.

For a locally compact group 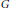$G$ and 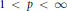$1\,<\,p\,<\,\infty $, let 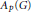${{A}_{p}}\left( G \right)$ be the Herz-Figà-Talamanca algebra and let $P{{M}_{p}}\left( G \right)$ be its dual Banach space. For a Banach 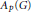${{A}_{p}}\left( G \right)$-module $X$ of 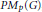$P{{M}_{p}}\left( G \right)$, we prove that the multiplier space 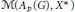$\text{M}\left( {{A}_{p}}\left( G \right),{{X}^{*}} \right)$ is the dual Banach space of 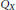${{Q}_{X}}$, where 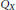${{Q}_{X}}$ is the norm closure of the linear span 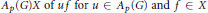${{A}_{p}}\left( G \right)X\,\text{of}\,u\,f\,\text{for}\,u\,\in \,{{A}_{p}}\left( G \right)\,\text{and}\,f\,\in \,X$ in the dual of 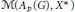$\text{M}\left( {{A}_{p}}\left( G \right),{{X}^{*}} \right)$. 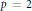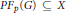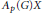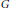If $p\,=\,2$ and $P{{F}_{p}}\left( G \right)\subseteq X$, then ${{A}_{p}}\left( G \right)X$ is closed in $X$ if and only if $G$ is amenable. In particular, we prove that the multiplier algebra 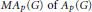$M{{A}_{p}}\left( G \right)\,\text{of}\,{{A}_{p}}\left( G \right)$ is the dual of 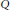$Q$, where 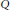$Q$ is the completion of 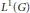${{L}^{1}}\left( G \right)$ in the 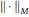$||\cdot |{{|}_{M}}$-norm. 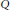$Q$ is characterized by the following: $f\,\in \,Q$ if an only if there are 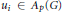${{u}_{i}}\,\in \,{{A}_{p}}\left( G \right)$ and 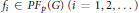${{f}_{i}}\in P{{F}_{p}}\left( G \right)\left( i=1,2,... \right)$ with 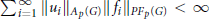$\sum\nolimits_{i=1}^{\infty }{||}\,{{u}_{i}}\,|{{|}_{{{A}_{p}}\left( G \right)}}||fi|{{|}_{P{{F}_{p}}\left( G \right)}}\,<\,\infty $ such that 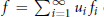$f=\sum{_{i=1}^{\infty }\,{{u}_{i}}{{f}_{i}}}$ on 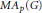$M{{A}_{p}}\left( G \right)$. It is also proved that if 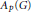${{A}_{p}}\left( G \right)$ is dense in 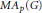$M{{A}_{p}}\left( G \right)$ in the associated 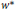${{w}^{*}}$-topology, then the multiplier norm and 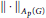$||\cdot |{{|}_{{{A}_{p}}\left( G \right)}}$-norm are equivalent on 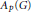${{A}_{p}}\left( G \right))$ if and only if 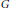$G$ is amenable.

Let $a$ be a natural number greater than 1. Let ${{f}_{a}}\left( n \right)$ be the order of $a\,\bmod \,n$. Denote by $\omega \left( n \right)$ the number of distinct prime factors of $n$. Assuming a weak form of the generalised Riemann hypothesis, we prove the following conjecture of Erdös and Pomerance:

The number of $n\,\le \,x$ coprime to a satisfying

$$\alpha \le \frac{\omega \left( {{f}_{a}}\left( n \right) \right)-{{\left( \log \,\log \,n \right)}^{2}}/2}{{{\left( \log \,\log \,n \right)}^{3/2}}/\sqrt{3}}\le \beta $$

is asymptotic to $\left( \frac{1}{\sqrt{2\pi }}\int_{\alpha }^{\beta }{{{e}^{-{{t}^{2}}/2}}}dt \right)\frac{x\phi \left( a \right)}{a}$ as $x$ tends to infinity.

In this paper we extend Darmon's theory of “integration on ${{\text{H}}_{p}}\times \text{H}$” to cusp forms $f$ of higher even weight. This enables us to prove a “weak exceptional zero conjecture”: that when the $p$-adic $L$-function of $f$ has an exceptional zero at the central point, the $\mathcal{L}$-invariant arising is independent of a twist by certain Dirichlet characters.

We construct analogues of theta series, Eisenstein series and Poincaré series for function fields of one variable over finite fields, and prove their basic properties.

We continue our investigation in [RST] of a martingale formed by picking a measurable set $A$ in a compact group $G$, taking random rotates of $A$, and considering measures of the resulting intersections, suitably normalized. Here we concentrate on the inverse problem of recognizing $A$ from a small amount of data from this martingale. This leads to problems in harmonic analysis on $G$, including an analysis of integrals of products of Gegenbauer polynomials.