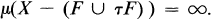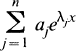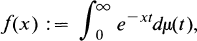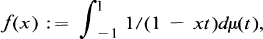Research Article
On the Analytic Continuation of c-Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 513-531
-
- Article
-
- You have access
- Export citation
Regularite De Fonctions Holomorphes Sur Des Wedges
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 532-545
-
- Article
-
- You have access
- Export citation
The Additive Characters of the Witt Ring of an Algebraic Number Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 546-588
-
- Article
-
- You have access
- Export citation
Linearization and Boundary Trajectories of Nonsmooth Control Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 589-609
-
- Article
-
- You have access
- Export citation
Pointwise Convergence of Alternating Sequences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 610-632
-
- Article
-
- You have access
- Export citation
Tensor Products of Fundamental Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 633-648
-
- Article
-
- You have access
- Export citation
On the Selmer Group of Twists of Elliptic Curves with Q-Rational Torsion Points
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 649-665
-
- Article
-
- You have access
- Export citation
The Quantificational Tangent Cones
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 666-694
-
- Article
-
- You have access
- Export citation
Some Differential Equations Related to Iteration Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 695-717
-
- Article
-
- You have access
- Export citation
On an F-Algebra of Holomorphic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 718-741
-
- Article
-
- You have access
- Export citation
Conjugates of Infinite Measure Preserving Transformations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 742-749
-
- Article
-
- You have access
- Export citation
Convergence of Interpolation to Transforms of Totally Positive Kernels
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 750-768
-
- Article
-
- You have access
- Export citation

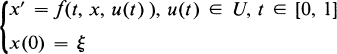
 and
and 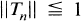 , where
, where 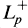 is the part of
is the part of 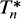 which is a positive linear contraction of
which is a positive linear contraction of 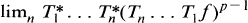
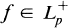 .
.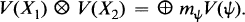
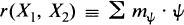
 (resp.
(resp. 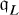 ). The completion of
). The completion of  is denoted by
is denoted by  . Let
. Let  one has
one has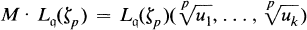
 . Here
. Here 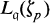 and
and  is the normed valuation belonging to
is the normed valuation belonging to  . In particular
. In particular 




 ,
,