Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T00:46:04.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Tensor Products of Fundamental Representations

Published online by Cambridge University Press:  20 November 2018

George Kempf  and
Linda Ness
George Kempf
Affiliation:
The Johns Hopkins University, Baltimore, Maryland
Linda Ness
Affiliation:
The Johns Hopkins University, Baltimore, Maryland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a reductive group over a field of characteristic zero. Fix a Borel subgroup B of G which contains a maximal torus T. For each dominant weight X we have an irreducible representation V(X) of G with highest weight X. For two dominant representation X1 and X2 we have a decomposition

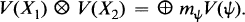
This decomposition is determined by the element

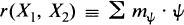
of the group ring of the group of characters of T.

The objective of this paper is to compute r(X1, X2) for all pairs X1 and X2 of fundamental weights. This will be used to compute the equations for cones over homogeneous spaces. This problem immediately reduces to the case when G has simple type; An, Bn, Cn, Dn, E6, E7, E8, F4 and G2. We will give complete details for the classical types. For the case An we will work with GLn.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 3 , 01 June 1988 , pp. 633 - 648
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Tensor products of representations of the general linear group, Amer. J. of Math. 109 (1987), 395–400.Google Scholar
2. Tensor products of representations, Amer. J. of Math. 109 (1987), 401–415.Google Scholar