Let 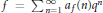 $f\,=\,\sum{_{n=1}^{\infty }{{a}_{f}}\left( n \right){{q}^{n}}}$ be a cusp form with integer weight
$f\,=\,\sum{_{n=1}^{\infty }{{a}_{f}}\left( n \right){{q}^{n}}}$ be a cusp form with integer weight 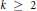 $k\,\ge \,2$ that is not a linear combination of forms with complex multiplication. For
$k\,\ge \,2$ that is not a linear combination of forms with complex multiplication. For 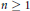 $n\,\ge \,1$, let
$n\,\ge \,1$, let
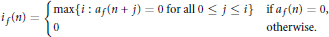 $${{i}_{f}}\left( n \right)\,=\,\left\{ _{0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{otherwise}\text{.}}^{\max \left\{ i\,:\,{{a}_{f}}\left( n+j \right)\,=\,0\,\text{for}\,\text{all}\,0\,\,\le \,j\,\le \,i \right\}\,\,\,\,\,\,\,\text{if}\,{{\text{a}}_{f}}\left( n \right)\,=\,0,} \right.\,$$
$${{i}_{f}}\left( n \right)\,=\,\left\{ _{0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{otherwise}\text{.}}^{\max \left\{ i\,:\,{{a}_{f}}\left( n+j \right)\,=\,0\,\text{for}\,\text{all}\,0\,\,\le \,j\,\le \,i \right\}\,\,\,\,\,\,\,\text{if}\,{{\text{a}}_{f}}\left( n \right)\,=\,0,} \right.\,$$
Concerning bounded values of 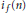 ${{i}_{f}}\left( n \right)$ we prove that for
${{i}_{f}}\left( n \right)$ we prove that for 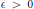 $\in \,>\,0$ there exists
$\in \,>\,0$ there exists 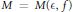 $M\,=\,M\left( \in ,\,f \right)$ such that
$M\,=\,M\left( \in ,\,f \right)$ such that 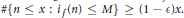 $\#\left\{ n\,\le \,x\,:\,{{i}_{f}}\left( n \right)\,\le \,M \right\}\,\ge \,\left( 1-\in \right)x.$ Using results of Wu, we show that if
$\#\left\{ n\,\le \,x\,:\,{{i}_{f}}\left( n \right)\,\le \,M \right\}\,\ge \,\left( 1-\in \right)x.$ Using results of Wu, we show that if 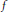 $f$ is a weight 2 cusp form for an elliptic curve without complex multiplication, then
$f$ is a weight 2 cusp form for an elliptic curve without complex multiplication, then 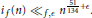 ${{i}_{f}}\left( n \right)\,{{\ll }_{f,\in }}\,{{n}^{\frac{51}{134}+\in }}$. Using a result of David and Pappalardi, we improve the exponent to
${{i}_{f}}\left( n \right)\,{{\ll }_{f,\in }}\,{{n}^{\frac{51}{134}+\in }}$. Using a result of David and Pappalardi, we improve the exponent to 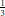 $\frac{1}{3}$ for almost all newforms associated to elliptic curves without complex multiplication. Inspired by a classical paper of Selberg, we also investigate
$\frac{1}{3}$ for almost all newforms associated to elliptic curves without complex multiplication. Inspired by a classical paper of Selberg, we also investigate 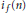 ${{i}_{f}}\left( n \right)$ on the average using well known bounds on the Riemann Zeta function.
${{i}_{f}}\left( n \right)$ on the average using well known bounds on the Riemann Zeta function.