Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:51:02.305Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Sizes of Gaps in the Fourier Expansion of Modular Forms

Published online by Cambridge University Press:  20 November 2018

Emre Alkan
Emre Alkan*
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, 61801, USA, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 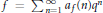$f\,=\,\sum{_{n=1}^{\infty }{{a}_{f}}\left( n \right){{q}^{n}}}$ be a cusp form with integer weight 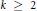$k\,\ge \,2$ that is not a linear combination of forms with complex multiplication. For 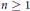$n\,\ge \,1$, let

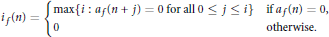$${{i}_{f}}\left( n \right)\,=\,\left\{ _{0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{otherwise}\text{.}}^{\max \left\{ i\,:\,{{a}_{f}}\left( n+j \right)\,=\,0\,\text{for}\,\text{all}\,0\,\,\le \,j\,\le \,i \right\}\,\,\,\,\,\,\,\text{if}\,{{\text{a}}_{f}}\left( n \right)\,=\,0,} \right.\,$$

Concerning bounded values of 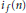${{i}_{f}}\left( n \right)$ we prove that for 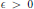$\in \,>\,0$ there exists 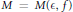$M\,=\,M\left( \in ,\,f \right)$ such that 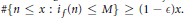$\#\left\{ n\,\le \,x\,:\,{{i}_{f}}\left( n \right)\,\le \,M \right\}\,\ge \,\left( 1-\in \right)x.$ Using results of Wu, we show that if 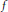$f$ is a weight 2 cusp form for an elliptic curve without complex multiplication, then 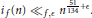${{i}_{f}}\left( n \right)\,{{\ll }_{f,\in }}\,{{n}^{\frac{51}{134}+\in }}$. Using a result of David and Pappalardi, we improve the exponent to 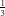$\frac{1}{3}$ for almost all newforms associated to elliptic curves without complex multiplication. Inspired by a classical paper of Selberg, we also investigate 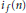${{i}_{f}}\left( n \right)$ on the average using well known bounds on the Riemann Zeta function.

Keywords

11F30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 3 , 01 June 2005 , pp. 449 - 470
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Alkan, E., Nonvanishing of Fourier coefficients of modular forms. Proc. Amer. Math. Soc. 131(2003), 1673–1680.Google Scholar
[2] Balog, A. and Ono, K., The Chebotarev density theorem in short intervals and some questions of Serre. J. Number Theory 91(2001), 356–371.Google Scholar
[3] David, C. and Pappalardi, F., Average Frobenius distributions of elliptic curves. Internat.Math. Res. Notices 4(1999), 165–183.Google Scholar
[4] Erdʺos, P., On the difference of consecutive terms of sequences defined by divisibility properties. Acta Arith. 12(1966), 175–182.Google Scholar
[5] Elkies, N., The existence of infinitely many supersingular primes for every elliptic curve over Q. Invent. Math. 89(1987), 561–567.Google Scholar
[6] Elkies, N., Distribution of supersingular primes. Astérisque 198-200(1992), 127–132.Google Scholar
[7] Fouvry, E. and Iwaniec, H., Exponential sums with monomials. J. Number Theory 33(1989), 311–333.Google Scholar
[8] Filaseta, M. and Trifonov, O., On gaps between squarefree numbers II. J. LondonMath. Soc. 45(1992), 215–221.Google Scholar
[9] Granville, A., ABC allows us to count squarefrees. Internat.Math. Res. Notices 19(1998), 991–1009.Google Scholar
[10] Iwaniec, H., Topics in Classical Automorphic Forms. Graduate Studies in Mathematics 17, American Mathematical Society, Providence, RI, 1997.Google Scholar
[11] Murty, V. K.,Modular forms and the Chebotarev density theorem II. In: Analytic Number Theory, LondonMath. Soc. Lecture Note Ser. 247, 1997, pp. 287–308.Google Scholar
[12] Serre, J. P., Quelques applications du théorème de densité de Chebotarev. Inst. Hautes Études Sci. Publ. Math. 54(1981), 323–401.Google Scholar
[13] Selberg, A., On the normal density of primes in small intervals, and the difference between consecutive primes. Arch. Math. Naturvid. 47(1943), 87–105.Google Scholar
[14] Sargos, P. and Wu, J., Multiple exponential sums with monomials and their applications in number theory. Acta Math. Hungar. 87(2000), 333–354.Google Scholar
[15] Titchmarsh, E C., The Theory of the Riemann Zeta-Function. Clarendon Press, Oxford, 1951.Google Scholar
[16] Titchmarsh, E C., Introduction to the theory of Fourier Integrals. Third edition. Chelsea Publishing Company, New York, 1986 Google Scholar
[17] Wan, D., On the Lang-Trotter conjecture. J. Number Theory 35(1990), 247–268.Google Scholar
[18] Wu, J., Nombres B-libres dans les petits intervalles. Acta Arith. 65(1993), 97–116.Google Scholar