Published online by Cambridge University Press: 20 November 2018
In the paper we formulate a Covering Property Axiom, 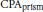 $\text{CP}{{\text{A}}_{\text{prism}}}$, which holds in the iterated perfect set model, and show that it implies the following facts, of which (a) and (b) are the generalizations of results of J. Steprāns.
$\text{CP}{{\text{A}}_{\text{prism}}}$, which holds in the iterated perfect set model, and show that it implies the following facts, of which (a) and (b) are the generalizations of results of J. Steprāns.
(a) There exists a family 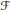 $\mathcal{F}$ of less than continuum many
$\mathcal{F}$ of less than continuum many 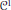 ${{C}^{1}}$ functions from
${{C}^{1}}$ functions from 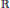 $\mathbb{R}$ to
$\mathbb{R}$ to 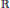 $\mathbb{R}$ such that
$\mathbb{R}$ such that 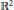 ${{\mathbb{R}}^{2}}$ is covered by functions from
${{\mathbb{R}}^{2}}$ is covered by functions from 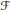 $\mathcal{F}$, in the sense that for every
$\mathcal{F}$, in the sense that for every 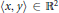 $\left\langle x,\,y \right\rangle \,\in \,{{\mathbb{R}}^{2}}$
$\left\langle x,\,y \right\rangle \,\in \,{{\mathbb{R}}^{2}}$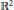 ${{\mathbb{R}}^{2}}$ there exists an
${{\mathbb{R}}^{2}}$ there exists an 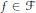 $f\,\in \,\mathcal{F}$ such that either
$f\,\in \,\mathcal{F}$ such that either 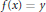 $f\left( x \right)\,=\,y$ or
$f\left( x \right)\,=\,y$ or 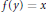 $f\left( y \right)\,=\,x$.
$f\left( y \right)\,=\,x$.
(b) For every Borel function 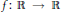 $f:\,\mathbb{R}\,\to \,\mathbb{R}$ there exists a family
$f:\,\mathbb{R}\,\to \,\mathbb{R}$ there exists a family 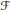 $\mathcal{F}$ of less than continuum many “
$\mathcal{F}$ of less than continuum many “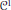 ${{C}^{1}}$” functions (i.e., differentiable functions with continuous derivatives, where derivative can be infinite) whose graphs cover the graph of
${{C}^{1}}$” functions (i.e., differentiable functions with continuous derivatives, where derivative can be infinite) whose graphs cover the graph of 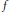 $f$.
$f$.
(c) For every 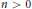 $n\,>\,0$ and a
$n\,>\,0$ and a 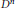 ${{D}^{n}}$ function
${{D}^{n}}$ function 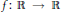 $f:\,\mathbb{R}\,\to \,\mathbb{R}$ there exists a family
$f:\,\mathbb{R}\,\to \,\mathbb{R}$ there exists a family 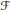 $\mathcal{F}$ of less than continuum many
$\mathcal{F}$ of less than continuum many 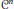 ${{C}^{n}}$ functions whose graphs cover the graph of
${{C}^{n}}$ functions whose graphs cover the graph of 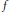 $f$.
$f$.
We also provide the examples showing that in the above properties the smoothness conditions are the best possible. Parts (b), (c), and the examples are closely related to work of A. Olevskiî.