Research Article
Function spaces on the unit circle
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 107-113
-
- Article
-
- You have access
- Export citation
A semigroup with an epimorphically embedded subband
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 231-242
-
- Article
-
- You have access
- Export citation
An inequality for the derivative of self-inversive polynomials
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 403-406
-
- Article
-
- You have access
- Export citation
Banach algebras with one dimensional radical
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 115-119
-
- Article
-
- You have access
- Export citation
Hilbert spaces have the Banach-Stone property for Bochner spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 121-128
-
- Article
-
- You have access
- Export citation
Transformation groups of strong characteristic 0
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 243-248
-
- Article
-
- You have access
- Export citation
An extension of the essential supremum concept with applications to normal integrands and multifunctions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 407-418
-
- Article
-
- You have access
- Export citation
Some saturated varieties of semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 419-425
-
- Article
-
- You have access
- Export citation
The K-functional of certain pairs of rearrangement invariant spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 249-257
-
- Article
-
- You have access
- Export citation
Krull dimension and torsion radicals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 129-138
-
- Article
-
- You have access
- Export citation
Time delays in n-species competition – I: Global stability in constant environments
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 427-441
-
- Article
-
- You have access
- Export citation
On an optimal control problem involving second order hyperbolic systems with boundary controls
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 139-148
-
- Article
-
- You have access
- Export citation
Atomic measure spaces and essentially normal composition operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 259-267
-
- Article
-
- You have access
- Export citation
On the embedding of processes in Brownian motion and the law of the iterated logarithm for reverse martingales
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 443-459
-
- Article
-
- You have access
- Export citation
On a functional differential equation in locally convex spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 269-283
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
The coupled diffusion of heat and moisture in bulk wool
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 149-150
-
- Article
-
- You have access
- Export citation
Research Article
On linear operators on ordered banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 285-305
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
Abstract dependence, recursion theory, and the lattice of recursively enumerable filters
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 461-464
-
- Article
-
- You have access
- Export citation
Series solutions for the profiles of axisymmetric fluid-liquid interfaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 151-152
-
- Article
-
- You have access
- Export citation
Relativistic fluid spheres
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 465-466
-
- Article
-
- You have access
- Export citation

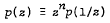 then
then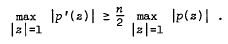
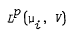 induces a Boolean isomorphism between the measure algebras
induces a Boolean isomorphism between the measure algebras 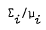 , thus generalizing a result of Cambern's for separable Hilbert spaces.
, thus generalizing a result of Cambern's for separable Hilbert spaces.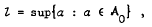
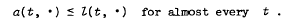


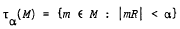 . Equivalent conditions for τ
. Equivalent conditions for τ