Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T02:21:51.390Z Has data issue: false hasContentIssue false
  • English
  • Français

Hilbert spaces have the Banach-Stone property for Bochner spaces

Published online by Cambridge University Press:  17 April 2009

Peter Greim
Peter Greim
Affiliation:
Mathematisches Institut, Freie Universität, Arnimallee 2–6, D 1000 Berlin 33, Germany.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (ωi, σi, μi.) be two positive finite measure spaces, V a non-zero Hilbert space, and 1 ≤ p < ∞, p # 2. In this article it is shown that each surjective linear isometry between the Bochner spaces 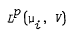induces a Boolean isomorphism between the measure algebras 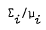, thus generalizing a result of Cambern's for separable Hilbert spaces.

This Banach–Stone type theorem is achieved via a description of the Lp-structure of .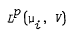

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 27 , Issue 1 , February 1983 , pp. 121 - 128
Copyright
Copyright © Australian Mathematical Society 1983

References

[1]Behrends, Ehrhard, M-structure and the Banach-Stone theorem (Lecture Notes in Mathematics, 736. Springer-Verlag, Berlin, Heidelberg, New York, 1979).Google Scholar
[2]Behrends, E., Danckwerts, R., Evans, R., Göbel, S., Greim, P., Meyfarth, K., Müller, W., Lp-structure in real Banaah spaces (Lecture Notes in Mathematics, 613. Springer-Verlag, Berlin, Heidelberg, New York, 1977).CrossRefGoogle Scholar
[3]Cambern, Michael, “The isometries of Lp(X, K)”, Pacific J. Math. 55 (1974), 9–17.CrossRefGoogle Scholar
[4]Cambern, Michael, “Isometries of measurable functions”, Bull. Austral. Math. Soc. 24 (1981), 13–26.CrossRefGoogle Scholar
[5]Diestel, J. and Uhl, J.J. Jr, Vector measures (Mathematical Surveys, 15. American Mathematical Society, Providence, Rhode Island, 1977).CrossRefGoogle Scholar
[6]Greim, Peter, “The centralizer of Bochner L∞-spaces”, Math. Ann. 260 (1982), 463–468.Google Scholar
[7]Greim, Peter, “Isometries and Lp-structure of separably valued Bochner Lp-spaces”, Measure theory and its applications (Proc. Conf. Sherbrooke, 1982. Lecture Notes in Mathematics. Springer-Verlag, Berlin, Heidelberg, New York, to appear).Google Scholar
[8]Lamperti, John, “On the isometries of certain function-spaces”, Pacific J. Math. 8 (1958), 459–466.CrossRefGoogle Scholar
[9]Sourour, A.R., “The isometries of L p (ω, X)”, J. Funct. Anal. 30 (1978), 276–285.CrossRefGoogle Scholar