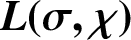 $\boldsymbol{L(\sigma ,\chi )}$
$\boldsymbol{L(\sigma ,\chi )}$
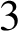 $3$
-MANIFOLDS IN
$3$
-MANIFOLDS IN
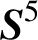 $\boldsymbol {S}^5$
$\boldsymbol {S}^5$