No CrossRef data available.
Published online by Cambridge University Press: 13 September 2021
We prove that for a Banach algebra A having a bounded
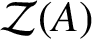 $\mathcal {Z}(A)$
-approximate identity and for every
$\mathcal {Z}(A)$
-approximate identity and for every
 $\mathbf {[IN]}$
group G with a weight w which is either constant on conjugacy classes or satisfies
$\mathbf {[IN]}$
group G with a weight w which is either constant on conjugacy classes or satisfies
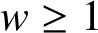 $w \geq 1$
,
$w \geq 1$
,
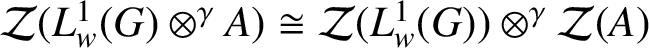 $\mathcal {Z}(L^{1}_{w}(G) \otimes ^{\gamma } A) \cong \mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\gamma } \mathcal {Z}(A)$
. As an application, we discuss the conditions under which
$\mathcal {Z}(L^{1}_{w}(G) \otimes ^{\gamma } A) \cong \mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\gamma } \mathcal {Z}(A)$
. As an application, we discuss the conditions under which
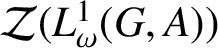 $\mathcal {Z}(L^{1}_{\omega }(G,A))$
enjoys certain Banach algebraic properties, such as weak amenability or semisimplicity.
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
enjoys certain Banach algebraic properties, such as weak amenability or semisimplicity.
Bharat Talwar is supported by a Senior Research Fellowship of CSIR (file number 09/045(1442)/ 2016-EMR-I).